LLM finetuning technical blog

LLM finetune technical blog

作者：@同济大学 刘越

Github ID：@miracle-techlink

联系邮箱：miracle.techlink@gmail.com

校内邮箱: 2254018@tongji.edu.cn

引言

随着大语言模型（LLM）规模的指数级增长，传统的全量微调方法正面临前所未有的挑战：参数量爆炸导致存储成本激增，灾难性遗忘阻碍多任务学习，计算资源需求超出大多数研究者的承受能力。为了在保持模型性能的同时大幅降低计算和存储开销，研究者们提出了各种参数高效微调（Parameter-Efficient Fine-Tuning, PELT）技术。

本文系统性地梳理了当前主流的LLM微调技术全景，从最基础的BitFit到工业级标配的LoRA，从学术探索的Prefix Tuning到实用的QLoRA，再到前沿的UniPELT等组合方法。每种技术都有其独特的适用场景和权衡考量：

• 轻量级方法（BitFit、Prompt Tuning）：专为资源极度受限的场景设计
• 平衡型方法（LoRA、Adapter）：在性能和效率间实现最佳平衡
• 组合型方法（UniPELT、MAM Adapter）：通过智能组合实现更优效果

通过深入剖析各方法的核心原理、数学基础、实现细节和实验对比，本文旨在为研究者和工程师提供一份全面的技术指南，帮助大家在具体应用场景中做出最优的技术选型。

---

BitFit 原理解析

概述

BitFit（论文：BitFit: Simple Parameter-efficient Fine-tuning or Transformer-based Masked Language-models）(link) 是一种极简的稀疏微调方法，其核心思想是仅训练模型的偏置参数，而将所有权重矩阵完全冻结。

在Transformer架构中，BitFit冻结所有transformer-encoder的权重参数，仅更新以下偏置参数：

• 注意力模块：query、key、value投影以及多头注意力合并时的偏置
• 前馈网络：MLP层中的偏置参数
• 层归一化：LayerNorm层的偏置参数
• 分类头：特定任务的分类层参数

令人惊讶的是，在BERT-Base/BERT-Large模型中，偏置参数仅占总参数量的0.08%～0.09%。然而，在BERT-Large模型上基于GLUE数据集的对比实验表明，BitFit在参数量远小于Adapter和Diff-Pruning的情况下，性能与这些方法相当，甚至在某些任务上略胜一筹。

数学原理

1. 预训练参数冻结
对任意线性算子
$$y=Wx+b$$
要求
$$W\leftarrow W_0（固定）$$仅允许 $b$ 成为可训练变量。

2. 可训练参数集合
$${\Theta }_{t}rain=b|b属于Transformer中所有bias项\cup w_{h}ead$$
$${\Theta }_{f}rozen={\Theta }_{t}otal{\Theta }_{t}rain$$

3. 前向计算（单层 Transformer）

• 自注意力
  $$Q=W_{q}x+b_q$$

  $$K=W_{k}x+b_k$$

  $$V=W_{v}x+b_v(W•冻结)$$

  $$Attn(Q,K,V)=softmax((Q{K}^{\top })/\surd d+mask)V$$

• 输出映射
  $$h_{a}ttn=W_{o}Attn+b_o$$

• FFN
  $$h_{f}f=W_2\sigma (W_1{h}_{a}ttn+b_1)+b_2(\sigma =GELU)$$

• LayerNorm
  $$y=LN(h_{f}f+h_{a}ttn)=\gamma \odot (z-\mu )/\sigma +b_{L}N$$

  仅$b_{L}N$ 训练

4. 目标函数
对数据集 $$D=(x_i,y_i)$$

$$L({\Theta }_{t}rain)={\Sigma }_i\ell (f(x_i;{\Theta }_{t}rain,{\Theta }_{f}rozen),y_i)$$

5. 梯度更新
仅对 ${\Theta }_{t}rain$ 内参数执行
$$b\leftarrow b-\eta \partial L/\partial b$$
对 $$W\in {\Theta }_{f}rozen$$有
$$\partial L/\partial W\equiv 0$$

6. 存储与部署
每个新任务只需保存
$${\Delta }_k=b_k\ast ,w_{h}ea{d}_k$$

$$\frac{|{\Delta }_k|}{|{\Theta }_{total}|}<0.1\%$$

推理时复用冻结 $W_0$，加载 $Δ_k $即可。

---

Prefix Tuning 原理

概述

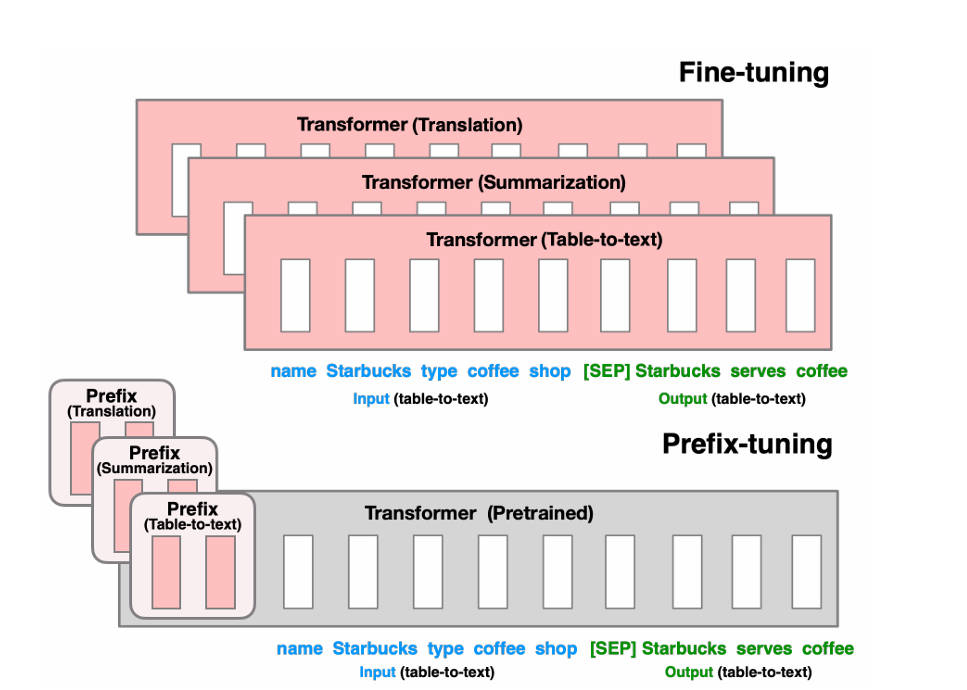
从图中可以清晰地看出，相比于全量微调需要更新整个模型的参数，每个垂直领域模型都需要大量计算资源和存储空间。Prefix Tuning的微调仅涉及前端的prefix块，冻结其余参数，实现了更高效节能且模块化的微调方式。

Prefix Tuning（论文：Prefix-Tuning: Optimizing Continuous Prompts for Generation）(link) 通过在输入token之前构造任务相关的虚拟token作为前缀，训练时仅更新Prefix部分的参数，而预训练语言模型的其他参数保持固定。针对不同的模型架构，需要构造相应的Prefix结构。

自回归架构模型：在句子前面添加前缀，得到 $z=[PREFIX;x;y]$，通过合适的上文在固定语言模型的情况下引导生成下文（类似于GPT-3的上下文学习机制）。

编码器-解码器架构模型：在Encoder和Decoder都增加前缀，得到 $z=[PREFIX;x;PREFIX0;y]$。Encoder端的前缀用于引导输入部分的编码，Decoder端的前缀用于引导后续token的生成，如下图所示。

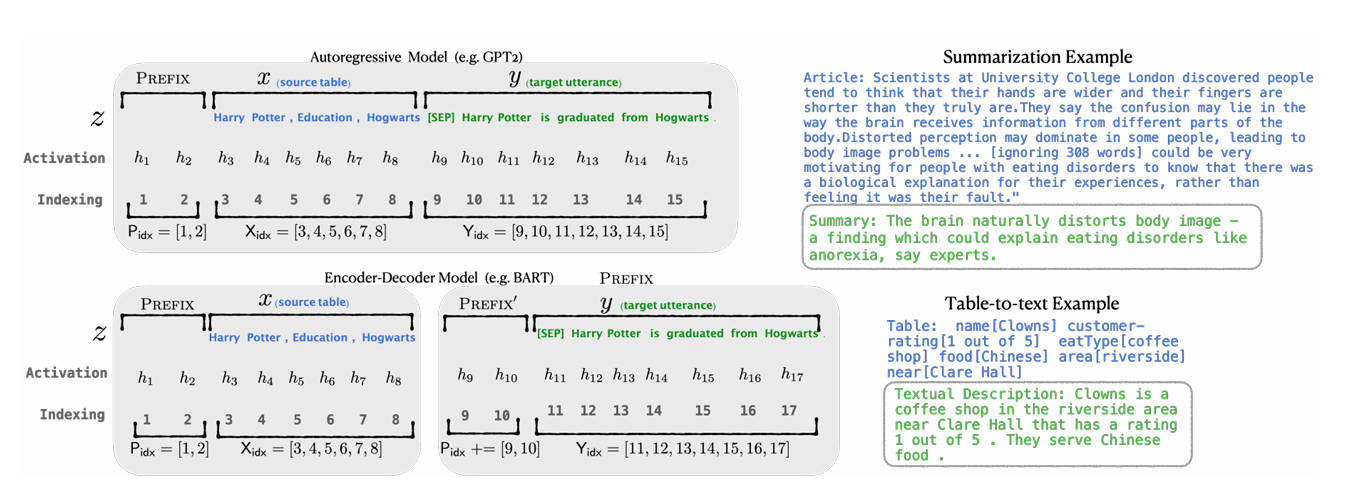
核心区别：与人工构造的"显式"Prompt不同，Prefix是可学习的"隐式"提示，能够通过梯度优化自动调整。

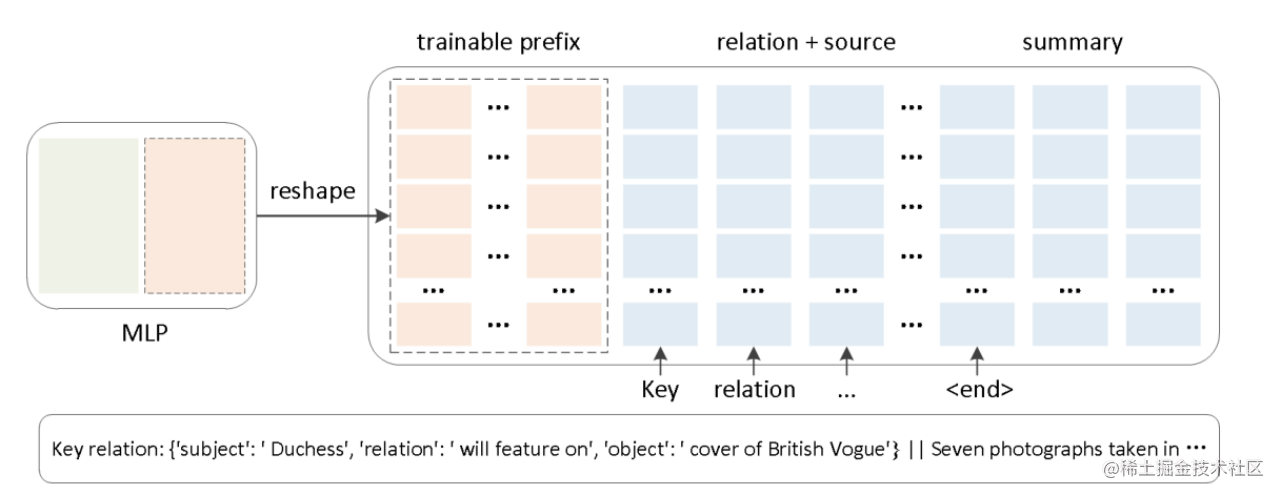
为防止直接更新Prefix参数导致训练不稳定，在Prefix层前添加MLP结构进行重参数化，训练完成后仅保留Prefix参数。

数学推理

1. 优化目标
与标准微调相同，最大化条件对数似然：
$$\underset{\theta }{\max }\log p_{\theta }(\mathbf{y}|\mathbf{x})=\sum _{i\in Y_{\text{idx}}}\log p_{\theta }(z_{i+1}|{\mathbf{h}}_{<i})$$

• 整个 Transformer 参数 $\varphi$ 被冻结
• 唯一可训练参数：前缀矩阵 $\theta =P_{\theta }\in {\mathbb{R}}^{|P|\times d}$

2. 前向递归关系
对任意位置 $i$：

[
h_i =
\begin{cases}
\mathrm{P}{\theta}[i, :], & i \in \mathcal{P}{\text{idx}} \[6pt]
\mathrm{Transformer}{\phi}(z_i, h{<i}), & \text{otherwise}
\end{cases}
]

解释：

• 若 $i$ 属于前缀区间，直接将 $P_{\theta }$ 对应行赋给 $h_i$（跳过 self-attention 计算）
• 否则走正常 Transformer 路径
• 前缀信息通过自注意力机制向右扩散

3. 下一步 token 分布
用最后一层激活计算 softmax 逻辑值：
$$p_{\theta }(z_{i+1}|h_{<i})=\text{softmax}(W_e{h}_i^{(L)})$$

• $h_i^{(L)}$：第 $L$ 层（最后一层）输出
• $W_e$：预训练词表映射矩阵（冻结）

4. 参数化技巧
为防止训练不稳定，引入重参数化：
$$P_{\theta }[i,:]={\text{MLP}}_{\theta }(P_0[i,:]),P_0\in {\mathbb{R}}^{|P|\times d^{\prime }},d^{\prime }\ll d$$

实际实现：

• 初始化 $P_0\sim \mathcal{N}(0,{\sigma }^2)$（$\sigma$ 很小，如 0.01）
• 两个线性层 + tanh：
  $${\text{MLP}}_{\theta }(u)=\tanh (u{W}_1)W_2,W_1\in {\mathbb{R}}^{d^{\prime }\times 512},W_2\in {\mathbb{R}}^{512\times d}$$
• 训练完成后只保留 MLP 输出，$P_0$ 可丢弃

5. 与离散 Prompt 的数学差异

离散 Prompt：
$$e_i=E[t_i],t_i\in \text{Vocab}$$

• 在输入层插入真实 token
• embedding 由冻结的 $E$ lookup 得到

Prefix Tuning：
$$e_i=P_{\theta }[i]\in {\mathbb{R}}^d$$

• 直接在连续空间优化
• 与词表无关
• 表达更丰富，梯度可直达前缀本身

6. 小结
Prefix Tuning = 冻结 Transformer，只训练一段可微前缀向量 $P_{\theta }$，通过自注意力向右传播，从而把生成方向"扳"到目标任务；为稳定训练，再用小矩阵+MLP重参数化。

---

Prompt Tuning 原理概述

大模型全量微调对每个任务训练一个模型，开销和部署成本都比较高。同时，离散的prompts（指人工设计prompts提示语加入到模型）方法，成本比较高，并且效果不太好。

基于此，作者提出了Prompt Tuning，通过反向传播更新参数来学习prompts，而不是人工设计prompts；同时冻结模型原始权重，只训练prompts参数，训练完以后，用同一个模型可以做多任务推理。

Prompt Tuning（论文：The Power of Scale for Parameter-Efficient Prompt Tuning） ，(link)该方法可以看作是Prefix Tuning的简化版本，它给每个任务定义了自己的Prompt，然后拼接到数据上作为输入，但只在输入层加入prompt tokens，并且不需要加入 MLP 进行调整来解决难训练的问题。

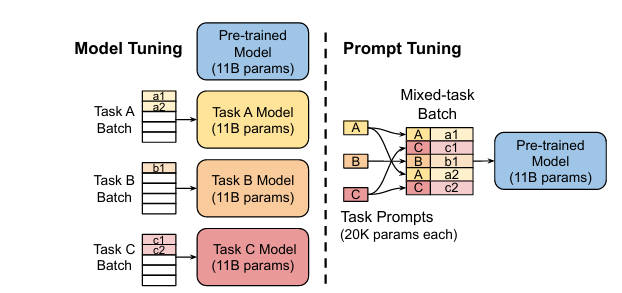
路线	参数量/任务	磁盘占用	效果趋势	一句话吐槽
Model Tuning	11B	×N	最佳	土豪玩法
Prompt Tuning	20K	≈0	≈最佳	环保神器
Mixed-task	0（增量）	1×11B	中	一锅乱炖，调参地狱

同时，Prompt Tuning 还提出了 Prompt Ensembling，也就是在一个批次（Batch）里同时训练同一个任务的不同 prompt（即采用多种不同方式询问同一个问题），这样相当于训练了不同模型，比模型集成的成本小多了。

---

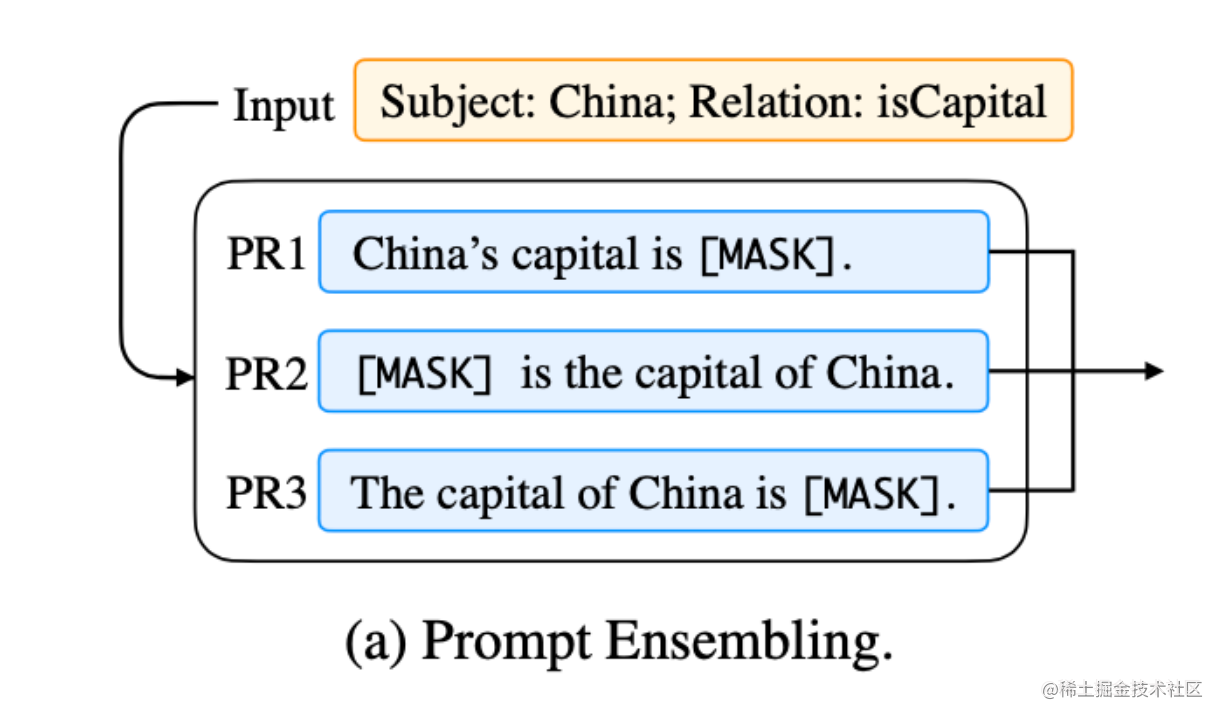
P-tuning and P-tuning V2 技术报告

P-tuning

该方法的提出主要是为了解决这样一个问题：大模型的Prompt构造方式严重影响下游任务的效果。比如：GPT-3采用人工构造的模版来做上下文学习（in context learning），但人工设计的模版的变化特别敏感，加一个词或者少一个词，或者变动位置都会造成比较大的变化。

同时，近来的自动化搜索模版工作成本也比较高，以前这种离散化的token的搜索出来的结果可能并不是最优的，导致性能不稳定。基于此，作者提出了P-Tuning，设计了一种连续可微的virtual token（同Prefix-Tuning类似）。

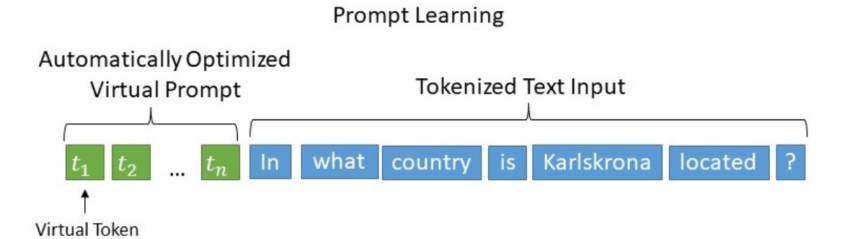
P-Tuning 把“靠人脑写 prompt”改成“靠梯度找 prompt”——用连续可微的虚拟 token代替离散文字，再套一个小型编码器（LSTM+MLP）让优化过程稳定，从而摆脱人工模板对词序、字数极度敏感的痛点，同时保持大模型参数全部冻结，仅需训练<0.1% 的提示向量即可在 NLU 任务上逼近全量微调效果。

P-Tuning（论文：GPT Understands, Too）(link)，该方法将Prompt转换为可以学习的Embedding层，并用MLP+LSTM的方式来对Prompt Embedding进行一层处理。

相比Prefix Tuning，P-Tuning加入的可微的virtual token，但仅限于输入层，没有在每一层都加；另外，virtual token的位置也不一定是前缀，插入的位置是可选的。这里的出发点实际是把传统人工设计模版中的真实token替换成可微的virtual token。

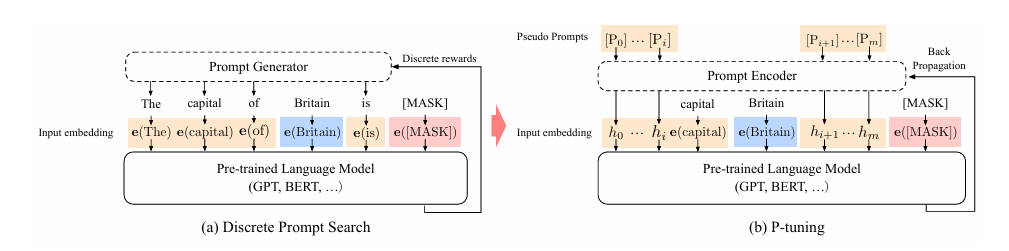
一句话：离散 prompt 是字典里挑词→靠运气；P-Tuning 是连续空间不断迭代最优→靠梯度。

维度	离散搜索	P-Tuning
搜索空间	词表（离散）	连续 ℝᵈ
优化方法	RL/遗传/Beam	梯度下降
梯度回传	❌	✅
稳定性	低，敏感	高，平滑
训练成本	高（采样多）	低（一次反向）

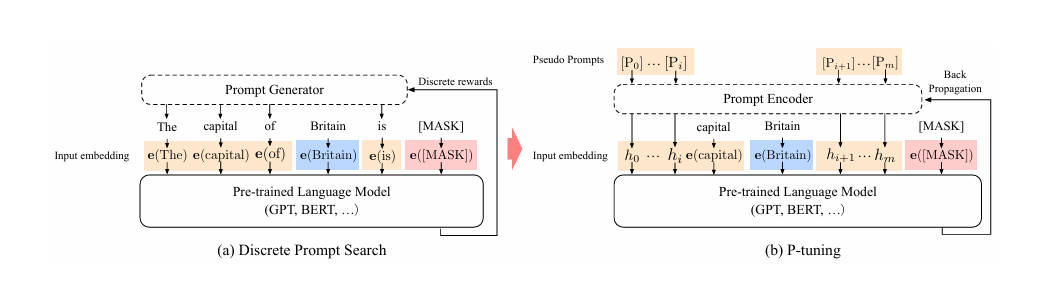
经过预训练的LM的词嵌入已经变得高度离散，如果随机初始化virtual token，容易优化到局部最优值，而这些virtual token理论是应该有相关关联的。因此，作者通过实验发现用一个prompt encoder来编码会收敛更快，效果更好。即用一个LSTM+MLP去编码这些virtual token以后，再输入到模型。

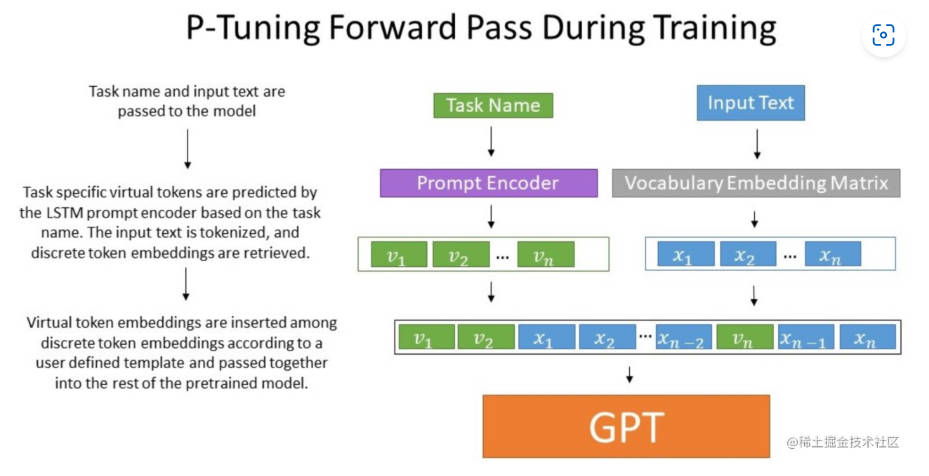
如图：任务名先过 LSTM 生成虚拟 token 向量，再按模板插到真实词语中间，一起送进冻结的 GPT。从对比实验证实看出，P-Tuning获得了与全参数一致的效果。甚至在某些任务上优于全参数微调。

P-tuning v2

不过之前的Prompt Tuning和P-Tuning等方法存在两个主要的问题：

第一，缺乏模型参数规模和任务通用性。

• 缺乏规模通用性：Prompt Tuning论文中表明当模型规模超过100亿个参数时，提示优化可以与全量微调相媲美。但是对于那些较小的模型（从100M到1B），提示优化和全量微调的表现有很大差异，这大大限制了提示优化的适用性。
• 缺乏任务普遍性：尽管Prompt Tuning和P-tuning在一些 NLU 基准测试中表现出优势，但提示调优对硬序列标记任务（即序列标注）的有效性尚未得到验证。

第二，缺少深度提示优化，在Prompt Tuning和P-tuning中，连续提示只被插入transformer第一层的输入embedding序列中，在接下来的transformer层中，插入连续提示的位置的embedding是由之前的transformer层计算出来的，这可能导致两个可能的优化挑战。

• 由于序列长度的限制，可调参数的数量是有限的。
• 输入embedding对模型预测只有相对间接的影响。

考虑到这些问题，作者提出了P-tuning v2，它利用深度提示优化（如：Prefix Tuning），对Prompt Tuning和P-Tuning进行改进，作为一个跨规模和NLU任务的通用解决方案。

-P-Tuning v2 的底层逻辑一句话：把“浅层小补丁”改成“深层大绷带”——
让可训练提示不再只飘在输入表面，而是像 Prefix Tuning 一样插到 Transformer 每一层，同时砍掉花哨重参、改用长度搜索 + 多任务预训练 + 传统分类头，最终让「提示调优」在 任意规模模型 + 任意 NLU 任务 上都能打平甚至超过全量微调。

---

Adapter Tuning 原理

概述

Adapter Tuning通过在Transformer每层插入"瓶颈式"可训练模块，在不触碰预训练权重的前提下，用极少的参数实现强大的任务迁移能力，是一种高效、模块化、可扩展的微调新范式。

Adapter Tuning（论文：Parameter-Efficient Transfer Learning for NLP）(link) 设计了专门的Adapter结构并嵌入Transformer架构中。针对每个Transformer层，在多头注意力投影之后和第二个前馈网络之后各增加一个Adapter结构。训练时冻结预训练模型参数，仅对新增的Adapter结构和LayerNorm层进行微调，确保训练高效性。

每当出现新的下游任务时，通过添加Adapter模块生成易于扩展的下游模型，有效避免全量微调与灾难性遗忘问题。

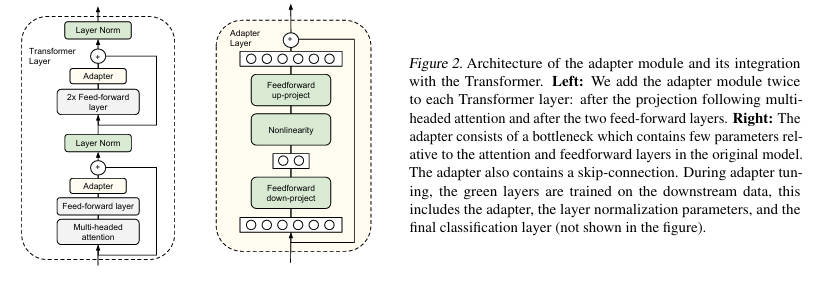
Adapter结构形象化：将Adapter比作"两头宽、中间窄的沙漏"：

• 入口：Transformer将维度d的"粗特征流"送入沙漏
• 瓶颈：down-project → 压缩到m维（m≪d）→ 非线性激活。这一窄腰决定"参数节省量"：参数量 ∝ d×m + m×d = 2dm
• 出口：up-project → 重新膨胀回d维，恢复原有通道宽度
• 残差连接：将入口原封不动地"跨桥"加到出口，形成残差。初始化时沙漏几乎不通（权重≈0），桥让整体≈恒等映射，确保训练起步稳定

数学推导

设：

• 输入向量：$x\in {\mathbb{R}}^d$
• 瓶颈维度：$m\in {\mathbb{N}}^{+}$，满足 $m\ll d$
• Down-project 参数：$W_{\downarrow }\in {\mathbb{R}}^{d\times m}$，$b_{\downarrow }\in {\mathbb{R}}^m$
• Up-project 参数：$W_{\uparrow }\in {\mathbb{R}}^{m\times d}$，$b_{\uparrow }\in {\mathbb{R}}^d$
• 激活函数：$\sigma :\mathbb{R}\to \mathbb{R}$（通常为 ReLU 或 GELU）

1. Down-project 降维
$$z=\sigma (x{W}_{\downarrow }+b_{\downarrow })\in {\mathbb{R}}^m$$

计算复杂度：

• 矩阵乘法：$x{W}_{\downarrow }$ 需要 $d\times m$ 次标量乘法
• 偏置加法：$m$ 次标量加法
• 激活函数：$m$ 次函数计算

2. Up-project 恢复维度
$$y=z{W}_{\uparrow }+b_{\uparrow }\in {\mathbb{R}}^d$$

计算复杂度：

• 矩阵乘法：$z{W}_{\uparrow }$ 需要 $m\times d$ 次标量乘法
• 偏置加法：$d$ 次标量加法

3. Skip-connection 残差连接
$$\text{out}=y+x\in {\mathbb{R}}^d$$

计算复杂度：

• 向量加法：$d$ 次标量加法

总计算复杂度:

标量乘法次数：
$$\text{Multiplications}=d\times m+m\times d=2dm$$

标量加法次数：
$$\text{Additions}=m+d+d=m+2d$$

激活函数计算次数：
$$\text{Activations}=m$$

由于 $m\ll d$，Adapter 的计算开销主要来源于 $2dm$ 次乘法，远小于全连接层的 $d^2$ 次乘法。

Adapter变种

Adapter技术衍生出多个变种，主要包括AdapterFusion和AdapterDrop，各自解决不同的实际问题：

方法	核心问题	解决方案
AdapterFusion	单个任务仅激活一个Adapter，无法利用跨任务共享信息	融合多个Adapter知识，提升目标任务表现
AdapterDrop	每层都插Adapter精度高，但推理时计算堆叠	丢弃不重要层的Adapter，加速推理并降低显存占用

步骤	AdapterFusion	AdapterDrop
训练阶段	① 先为 N 个任务各自训练独立 Adapter（冻结主模型） ② 新增Fusion 模块（注意力式权重），在目标 task 数据上继续训练（仍冻主模型）	正常训练若干层 Adapter（可全部保留）
推理阶段	保留全部 Adapter + Fusion 权重；前向时加权融合各任务 Adapter 输出	根据任务/资源预算提前剪掉若干层的 Adapter（只剩 Identity 或完全去掉），主模型与剩余 Adapter 照常前向
新增参数	Fusion 矩阵 Q,K,V ∈ ℝ^{d×d}，每层一套，≈ 3d²/层	无新增参数，剪掉的层直接消失

AdapterFusion

AdapterFusion（论文：AdapterFusion:Non-Destructive Task Composition for Transfer Learning）(link) 是一种融合多任务信息的Adapter变体，在标准Adapter基础上进行优化，通过两阶段学习过程提升下游任务表现。

两阶段学习框架：

• 知识提取阶段：在不同任务下引入各自的Adapter模块，学习特定任务信息
• 知识组合阶段：固定预训练模型参数与特定任务Adapter参数，引入新参数（AdapterFusion）学习组合多个Adapter中的知识，提升模型在目标任务中的表现

第一阶段训练方式：

• 单任务Adapter（ST-A）：N个任务分别独立优化，各任务间互不干扰
• 多任务Adapter（MT-A）：N个任务通过多任务学习进行联合优化

第二阶段设计：为避免引入特定任务参数导致的灾难性遗忘，AdapterFusion提出共享多任务信息结构。针对特定任务m，AdapterFusion联合第一阶段训练得到的N个Adapter信息，固定语言模型参数和N个Adapter参数，新引入AdapterFusion参数，目标函数学习针对特定任务m的AdapterFusion参数。
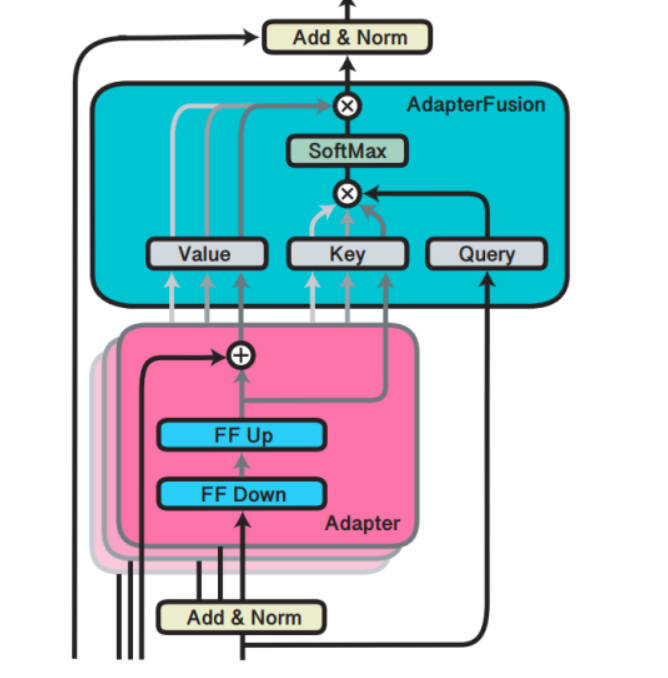
AdapterFusion结构：本质上是一个注意力机制，参数包括query、key、value矩阵，在Transformer每一层都存在。其query是Transformer各子模块的输出结果，key和value则是N个任务Adapter的输出。通过AdapterFusion，模型可为不同任务对应的Adapter分配不同权重，聚合N个任务信息，为特定任务输出更合适的结果。

AdapterDrop

AdapterDrop（论文：AdapterDrop: On the Efficiency of Adapters in Transformers[(link)]）(https://arxiv.org/pdf/2010.11918)，在不影响任务性能的情况下，对Adapter动态高效的移除，尽可能的减少模型的参数量，提高模型在反向传播（训练）和正向传播（推理）时的效率。

① 重要性估计（离线，零参数）

设模型共 $L$ 层，每层 Adapter 参数为 ${\Theta }_l$（仅含该层 Adapter 权重）。

在验证集 ${\mathcal{D}}_{\text{val}}$ 上做一次前向-反向传播：

$$g_l={\Vert \frac{\partial \mathcal{L}}{\partial {\Theta }_l}\Vert }_2\text{(梯度 L2 范数，标量)}$$

剪枝判据：

• 阈值法：若 $g_l<\epsilon$，则层 $l\in S_{\text{cut}}$（待剪集合）
• 排序法：取 $g_l$ 最小的 $\lfloor \alpha L\rfloor$ 层，$\alpha \in [0.2,0.5]$

② 结构剪枝（训练前一次性）

定义剪枝掩码：
$$m_l=\{\begin{array}{ll}0& \text{若 }l\in S_{\text{cut}}\\ 1& \text{否则}\end{array}$$

前向函数变为：
$$\begin{array}{rl}{\text{Adapter}}_l(x)& =m_l\cdot \text{Bottleneck}(x)+(1-m_l)\cdot x\\ & =\{\begin{array}{ll}\text{Bottleneck}(x)& l\text{ 保留}\\ x& l\text{ 被剪}\end{array}\end{array}$$

其中标准 Adapter 计算：
$$\text{Bottleneck}(x)=W_{\uparrow }\cdot \sigma (W_{\downarrow }x+b_{\downarrow })+b_{\uparrow }$$

参数量立即降为：
$$|{\Theta }_{\text{adapter}}|=\sum _{l=1}^L{m}_l\cdot (2dm+d+m)$$

③ 训练 / 推理（无运行时开销）

损失函数只含剩余参数：
L ( θ ) = ∑ ( x , y ) ∈ D ℓ ( f Θ frozen , { Θ l } m l = 1 ( x ) , y ) \mathcal{L}(\theta) = \sum_{(x,y) \in \mathcal{D}} \ell\left(f_{\Theta_{\text{frozen}}, \{\Theta_l\}_{m_l=1}}(x), y\right) L(θ)=(x,y)∈D∑​ℓ(fΘfrozen​,{Θl​}ml​=1​​(x),y)

梯度仅沿 $m_l=1$ 的层传播：
$${\nabla }_{{\Theta }_l}\mathcal{L}=0\text{当 }{m}_l=0$$

计算复杂度变化：

• 前向计算量 FLOPs 从 $O(L\cdot 2dm)$ 降至 $O((L-|S_{\text{cut}}|)\cdot 2dm)$
• 显存占用同理下降

---

LoRA及其变体原理

LoRA

LoRA（论文：LoRA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS）(link) 的核心思想是通过低秩分解模拟参数变化量，以极小的参数量实现大模型的间接训练。

在涉及矩阵相乘的模块中，在原始预训练语言模型旁增加新的通路，通过前后两个矩阵A、B相乘实现：第一个矩阵A负责降维，第二个矩阵B负责升维，中间层维度为r，从而模拟所谓的本征秩（intrinsic rank）。

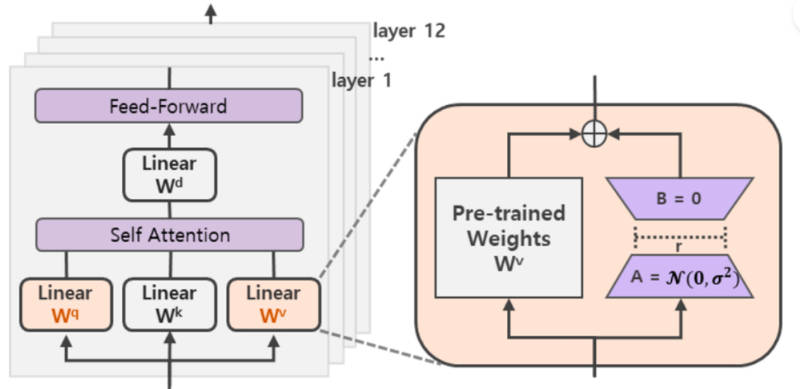
可训练层维度与预训练模型层维度一致为d，先将维度d通过全连接层降维至r，再从r通过全连接层映射回d维度，其中r<<d，r是矩阵的秩。这样矩阵计算从d×d变为d×r + r×d，参数量大幅减少。

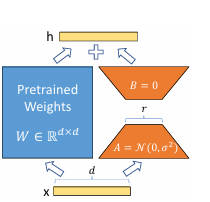
1. 低秩分解
对预训练权重矩阵 $W_0\in {\mathbb{R}}^{d\times d}$ 不做任何改动，仅在其旁路引入增量：
$$\Delta W\triangleq BA,B\in {\mathbb{R}}^{d\times r},A\in {\mathbb{R}}^{r\times d},r\ll d.$$
右侧是两个瘦矩阵的乘积，$\text{rank}(\Delta W)\le r$ 恒成立，故称本征秩（intrinsic rank）。

2. 前向传播
$$h=W_{0}x+\Delta Wx=W_{0}x+B(Ax),x\in {\mathbb{R}}^d.$$
计算复杂度从 $O(d^2)$ 降为 $O(2dr)$。

3. 训练与合并

• 训练阶段：仅更新 { A , B } \{A,B\} {A,B}，$W_0$ 冻结；梯度 ${\nabla }_{A,B}\mathcal{L}$ 通过旁路回流
• 推理阶段：一次性合并
  $$W^{\prime }=W_0+BA\in {\mathbb{R}}^{d\times d},$$
  之后不再保留分解形式，计算图与原始模型完全重合

4. 秩的含义
矩阵乘积 $BA$ 的列空间由 $B$ 的 $r$ 个列向量张成，行空间由 $A$ 的 $r$ 个行向量张成，因此：
$$\text{rank}(\Delta W)\le r\ll d.$$
LoRA假设任务特定的权重扰动存在于极低维子空间中，仅需优化这 $r$ 个基方向即可复现全秩微调效果，从而将可训参数量从 $d^2$ 压缩到 $2dr$。

AdaLoRA

AdaLoRA是"会自己剪枝的LoRA"。基于前面介绍的Adapter和LoRA，AdaLoRA将每个增量矩阵∆W视为一棵"奇异值树"，训练过程中不断对树进行评分→修剪细枝→保留主干，让重要的矩阵分配更多秩，不重要的自动削减秩，全程无需人工指定r，最终用更少参数获得更高精度。

1. 问题形式化
对预训练权重 $W_0\in {\mathbb{R}}^{d\times d}$ 不做修改，仅通过低秩增量适配下游任务：
$$W=W_0+\Delta W,\Delta W\in {\mathbb{R}}^{d\times d},\text{rank}(\Delta W)\le R_{\text{max}}$$
经典 LoRA 固定 $\text{rank}(\Delta W)=r$；AdaLoRA 让 $\text{rank}(\Delta W)$ 动态变化，并在所有层所有矩阵之间共享总参数预算 $B$（以参数量或 FLOP 计）。

2. 增量参数化：奇异值分解视角
为避免“先全量 SVD 再剪”的巨大开销，AdaLoRA 采用显式奇异向量-值参数化：
$$\Delta W(t)=P(t)\Lambda (t)Q^{\top }(t)$$
其中 $P\in {\mathbb{R}}^{d\times k},Q\in {\mathbb{R}}^{d\times k}$ 为正交奇异向量（$k\le R_{\text{max}}$ 初始窗口），$\Lambda =\text{diag}({\lambda }_1,\dots ,{\lambda }_k)$ 为可训练奇异值。总参数量 $k(2d+1)\approx 2dk$ 预算可控；训练过程中 $k$ 逐步减小，实现结构化剪秩。

3. 自适应预算分配：重要性分数与剪枝
对每个奇异值 ${\lambda }_i$ 计算灵敏度（零阶近似）：

$$s_i=|{\lambda }_i\cdot {\nabla }_{{\lambda }_i}L|$$

每 $\Delta T$ 步将 { s i } i = 1 k \{s_i\}_{i=1}^k {si​}i=1k​ 降序排列，保留预算允许的前 $r^{\prime }$ 个：

r ′ = max ⁡ { r ∣ k ( 2 d + 1 ) ≤ B ( t ) } r' = \max\{ r \mid k(2d + 1) \le B(t) \} r′=max{r∣k(2d+1)≤B(t)}

$B(t)$ 为当前全局预算（可线性衰减）；删除对应 ${\lambda }_{r^{\prime }+1},\dots ,{\lambda }_k$ 及其向量列：

$$P\leftarrow P_{:,1:r^{\prime }},\Lambda \leftarrow {\Lambda }_{1:r^{\prime },1:r^{\prime }},Q\leftarrow Q_{:,1:r^{\prime }}$$

剩余奇异值/向量继续训练，实现「重要高秩，不重要低秩甚至零秩」的动态分配。

4. 正交约束与正则项
为避免显式硬正交带来的 SVD 开销，添加软惩罚：

$$L_{\text{orth}}=\Vert P^{\top }P-I{\Vert }_F^2+\Vert Q^{\top }Q-I{\Vert }_F^2$$

总损失：

$$L_{\text{total}}=L_{\text{task}}+\beta L_{\text{orth}},\beta \sim 10^{-4}$$

实验表明足以保持数值正交。

5. 预算调度（可选）
全局参数预算 $B(t)$ 可按线性或余弦 schedule 从初始 $B_{\text{max}}$ 减到 $B_{\text{min}}$：
$$B(t)=B_{\text{min}}+(B_{\text{max}}-B_{\text{min}})\left(1-\frac{t}{T}\right)$$
剪枝阈值随之收紧，实现渐进式稀疏化。

6. 理论性质

• 秩动态范围：$1\le \text{rank}(\Delta W)\le R_{\text{max}}$，且各矩阵独立决定
• 参数量上界：${\sum }_{\text{layers}}{r}_l(2d+1)\le B(t)$（硬预算约束）
• 收敛性：删除的是小奇异值，对损失函数的一阶影响期望为 0，训练稳定

QLoRA

QLoRA：将"模型压缩到4bit + 套用LoRA + GPU显存不足时优化器分页到内存"的三重优化技术。

核心思想：用4bit存储权重，用16bit计算梯度，用LoRA训练适配器，用分页内存兜底，最终实现48GB显卡微调65B模型，速度几乎无损失。

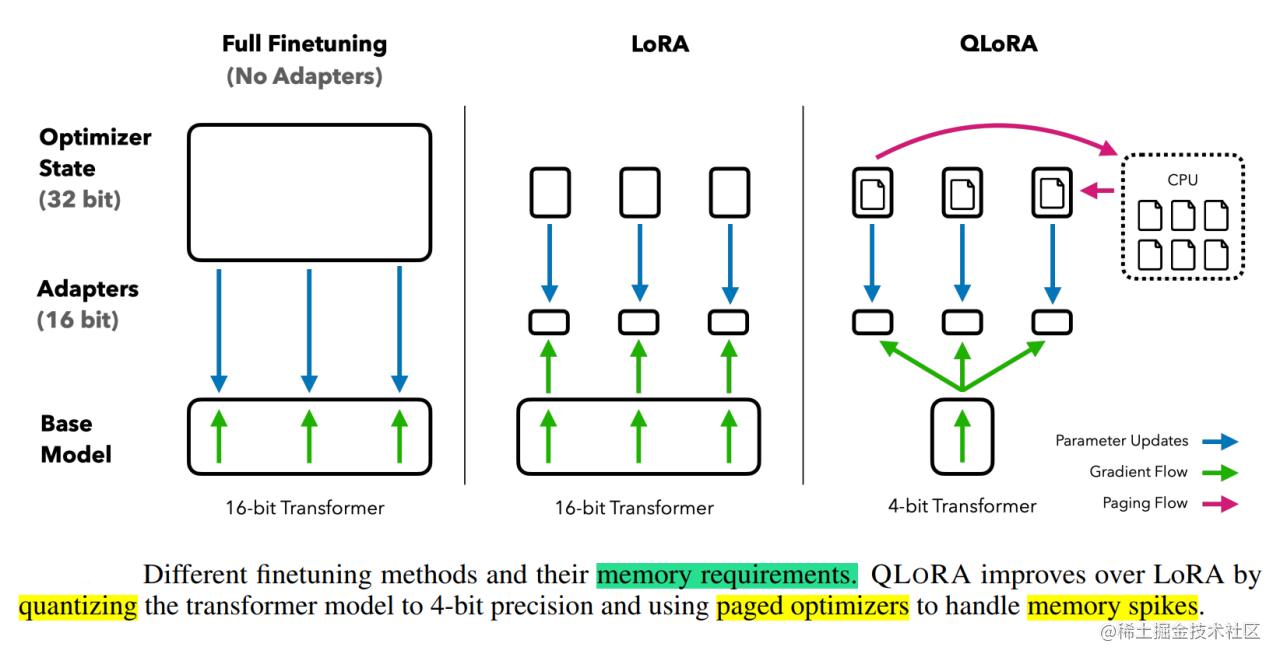
① 4-bit NormalFloat (NF4)
给定预训练权重 $W\sim \mathcal{N}(0,{\sigma }^2)$，传统均匀量化在分布尾部浪费码字。NF4 构造信息论最优 4-bit 码本：

1. 归一化：$\tilde{w}=w/\sigma$
2. 按累积分布函数等分 16 段：$q_i=F^{-1}(i/16),i=0\dots 16$
3. 每段期望码字：KaTeX parse error: Expected 'EOF', got '&' at position 85: … \le \tilde{w} &̲lt; q_{i+1}]

量化映射：
$$\hat{w}=\text{NF4}(w)=\sigma \cdot c_i,c_i=\text{centroid of }[q_i,q_{i+1})$$
实验显示重建误差 $\mathbb{E}[|w-\hat{w}|]$ 比 INT4/Fp4 降低 13–28 %。

② 双量化（Double Quantization）
第一次量化产生 32-bit 常量：
$$s=\frac{\max |W|}{2^{15}},z=\text{zero-point}$$
对 $(s,z)$ 再进行 8-bit 量化：
$$\hat{s}={\text{Quant}}_8(s),\hat{z}={\text{Quant}}_8(z)$$
存储成本从 64 bit 降至 16 bit，节省 ≈ 0.4 bit/参数；对 65 B 模型约减少 3 GB 常量存储。

③ 计算流程：存 4 bit，算 16 bit
权重张量常驻显存格式： NF4 ∈ { 0 , 1 } 4   bit \text{NF4} \in \{0,1\}^{4\,\text{bit}} NF4∈{0,1}4bit

前向单次流程：

$$W_{\text{bf16}}={\text{DeQuant}}_{\text{NF4→BF16}}(\text{NF4};\hat{s},\hat{z})$$

$$H=W_{\text{bf16}}\cdot X(\text{cublasLt, BF16 GEMM})$$

$$\Delta H=BA\cdot X(\text{LoRA branch, BF16})$$

$$Y=H+\Delta H$$

反向仅更新 LoRA 参数 { A , B } \{A,B\} {A,B}；量化权重无梯度路径，显存占用恒定为 4 bit 权重 + 2dr BF16 适配器。

④ 分页优化器（Paged Optimizer）
利用 NVIDIA UVM 为 Adam 状态分配页锁定内存：

• 动量 & 方差张量：$M,V\in {\mathbb{R}}^{P\times \text{BF16}}$
• 当 GPU 显存不足时，驱动按页粒度自动换出到 CPU DRAM；更新前再换入。

内存需求模型：

$${\text{Mem}}_{\text{total}}=\underset{\text{weights}}{\underbrace{\frac{1}{2}\text{NF4}(P)}}+\underset{\text{LoRA}}{\underbrace{2dr}}+\underset{\text{activation}}{\underbrace{\text{Act}}}+\underset{\text{optimizer}}{\underbrace{\text{Paged}(2P)}}$$

实验显示在 48 GB A6000 上微调 LLaMA-65B 无 OOM，吞吐下降 < 5 %。

---

混合微调——组合方法

MAM Adapter统一框架

近年来涌现出多种参数高效的迁移学习方法，这些方法仅需微调少量额外参数即可获得强大性能。虽然效果显著，但人们对这些方法为何有效的关键要素以及各种高效微调方法间的内在联系仍知之甚少。

下图展示了不同微调方法在XSum数据集上进行英文文本摘要任务的效果（ROUGE-2为评价指标，越大越好）以及各高效微调方法参数量相对于全参数微调参数量的百分比。图中左上角位置代表理想化方法。从图中可发现，Adapter、Prefix Tuning和LoRA都是性能较好的方法。

核心疑问：为什么看起来Adapter、Prefix Tuning、LoRA在结构和公式上都不太一样，尤其是Prefix Tuning，但这三种方法却有近似的效果？

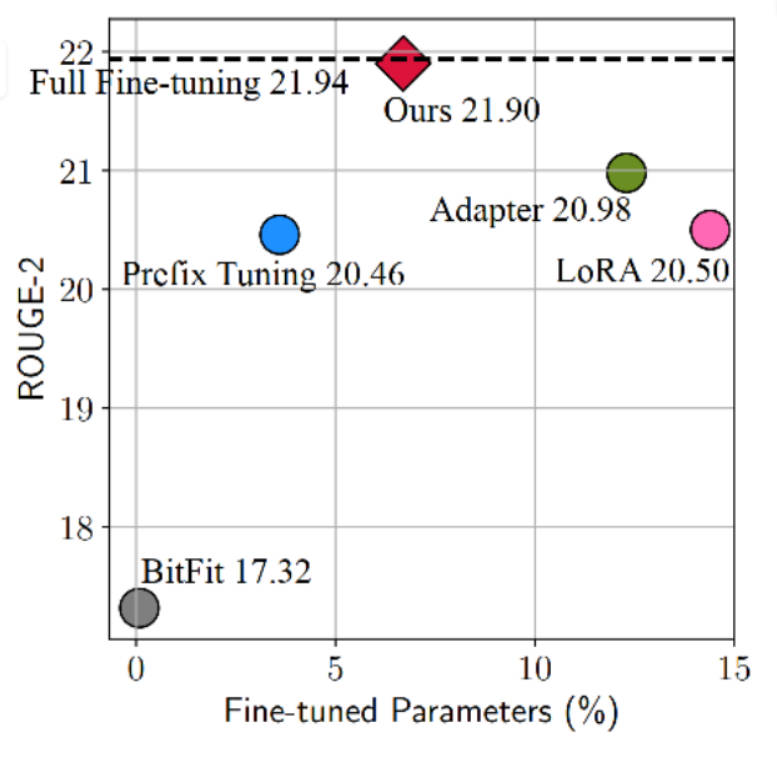
基于此，研究者分解了当前最先进的参数高效迁移学习方法（Adapter、Prefix Tuning和LoRA）的设计，提出了MAM Adapter（论文：Towards a Unified View of Parameter-Efficient Transfer Learning）(link)，一个在它们之间建立联系的统一框架。具体而言，将这些方法重新构建为对预训练模型中特定隐藏状态的修改，并定义一组设计维度，不同方法沿着这些维度变化。

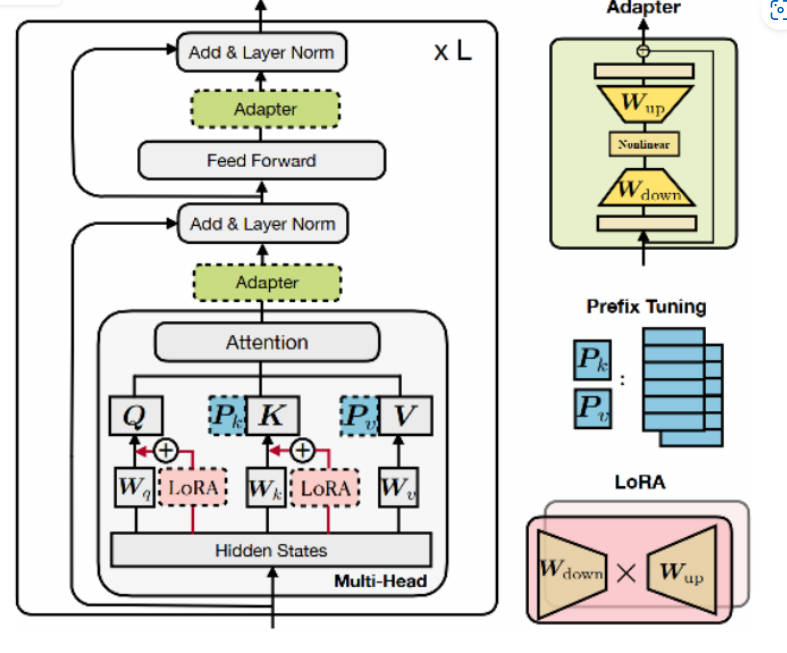
首先，作者通过对Prefix Tuning变换，发现Prefix Tuning和Adapters的公式高度相似。

然后，分析不同微调方法的内部结构和结构插入形式的相似之处。下图展示了高效微调方法Adapter、Prefix Tuning、LoRA以及新变体（通过更换一些元素，设计了前人的工作里没有的变体） Parallel Adapter、 Scaled PA的结构。

下表展示了高效微调方法Adapter、Prefix Tuning、LoRA以及新变体在新增可训练参数结构形式（functional form）、结构插入形式（Insertion form）、新增结构在PLM修改的具体位置（modified representation）、新增结构与PLM的组合函数（composition function）。其中，新增可训练参数结构形式为需要学习的部分（注：Prefix Tuning为经过转换后的格式）；插入形式有串联或并联；模型修改的具体位置有Attention、FFN层。

UniPELT 门控组合

UniPELT（论文：UNIPELT: A Unified Framework for Parameter-Efficient Language Model Tuning）(link) 是LoRA、Prefix Tuning和Adapter的智能门控组合。

具体实现：LoRA重新参数化用于WQ和WV注意力矩阵，Prefix Tuning应用于每一Transformer层的key和value，并在Transformer块的前馈子层之后添加Adapter。对于每个模块，门控通过线性层实现：GP参数控制Prefix-tuning开关，GL控制LoRA开关，GA控制Adapter开关。可训练参数包括LoRA矩阵WA（Down）和WB（Up）、提示调优参数Pk和Pv、Adapter参数和门函数权重。图中蓝色参数为可学习参数。

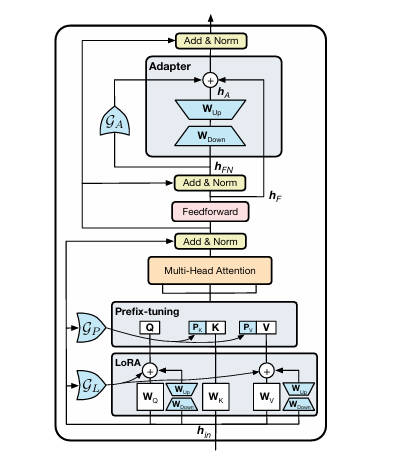
UniPELT 的本质： 把三条参数高效微调（PELT）旁路塞进一个 Transformer，再用可学习门控按需“打开”，让数据自己决定“谁有用谁上”。整个框架无侵入、无新算子，只需在原有 LoRA/Prefix/Adapter 上各乘一个 0-1 软开关，即可在 <10 % 参数 预算下，低数据场景 +2~3 点，高数据场景≥最佳单模块。

1. 设计目标

• 统一：一套代码同时承载 LoRA、Prefix Tuning、Adapter
• 自选择：任务/数据自己决定激活哪条旁路，避免人工调方法
• 预算硬约束：总新增参数量 ≤ 给定 B（例如 0.5 B 的 8 %）

2. 门控旁路形式化
对任意 Transformer 子层输入 $x$（维度 $d$），三条旁路并行计算：

旁路	数学形式	插入位置	本征参数量
LoRA	$\Delta h_L=B_L{A}_{L}x$	$W_Q,W_V$ 投影	$2dr$
Prefix	$\Delta h_P=\text{Attn}(x;P_k,P_v)$	Key/Value 前拼接	$2\cdot {\text{len}}_P\cdot d$
Adapter	$\Delta h_A={\text{MLP}}_{\downarrow \uparrow }(x)$	FFN 输出后相加	$2d\cdot m$

门控输出（线性 + Sigmoid）：

$$g_L(x)=\sigma (w_L^{\top }x),g_P(x)=\sigma (w_P^{\top }x),g_A(x)=\sigma (w_A^{\top }x)$$

最终隐藏状态更新：

$$x\leftarrow x+g_L\cdot \Delta h_L+g_P\cdot \Delta h_P+g_A\cdot \Delta h_A$$

所有门控权重 { w L , w P , w A } \{w_L, w_P, w_A\} {wL​,wP​,wA​} 与对应旁路参数联合训练，其余预训练权重冻结。

3. 预算硬约束实现

• 初始化：每条旁路按最小秩/长度/m 初始化
• 训练期：若某旁路门控均值 $<ϵ$（≈0.01）连续 $k$ 步，整个旁路参数被掩零并停止梯度 → 实际参数量 ↓
• 推理期：门控≈{0,1}，只保留激活旁路，其余从计算图移除 → 推理延迟可控

预算上限：

$${\text{Param}}_{\text{new}}\le \underset{\text{LoRA}}{\underbrace{2dr}}+\underset{\text{Prefix}}{\underbrace{2\cdot {\text{len}}_P\cdot d}}+\underset{\text{Adapter}}{\underbrace{2dm}}+\underset{\text{gates}}{\underbrace{3d}}\le B$$

对比

维度	MAM Adapter (手工乐高)	UniPELT (门控乐高)
混合动机	拆解 Adapter/Prefix/LoRA 的设计维度，发现“FFN 并行 Adapter + 注意力软提示”互补	同一任务上不同 PELT 方法表现方差大，需数据驱动的“谁有用谁上”
模块抽象	功能形式、插入位置、组合方式三张表 → 固定拼法	将 Adapter、Prefix、LoRA 视为三条可学习旁路，各加 0-1 门控
数学表述	前向：$$h=\text{FFN}(x)+\underset{\text{并行 Adapter}}{\underbrace{A_{\text{FFN}}\sigma (B_{\text{FFN}}x)}}+\underset{\text{Prefix}}{\underbrace{\text{Attn}(x;P)}}$$ 参数：$$\Vert A\Vert +\Vert P\Vert \le 6.7$$	门控：$$g_P=\sigma (w_P^{\top }x),g_L=\sigma (w_L^{\top }x),g_A=\sigma (w_A^{\top }x)$$ 前向：$$h=g_L\cdot \text{LoRA}(x)+g_P\cdot \text{Prefix}(x)+g_A\cdot \text{Adapter}(x)+x$$ 总参数量: $$\Vert LoRA\Vert +\Vert Prefix\Vert +\Vert Adapter\Vert +3d\le 0.1$$
分配策略	人工分析 → 固定预算：FFN-Adapter 主力，Prefix 辅助	数据驱动 → 可学习门控：高得分模块自动多分参，其余近似关闭
插入位置	FFN 并行 + Attention 前缀（互不重叠）	LoRA@WQ/WV，Prefix@K/V，Adapter@FFN-out（子空间正交）
训练信号	梯度同时更新 Adapter 权重 A,B 与 Prefix 向量 P	梯度更新 {A,B,P,门控权重}；门控≈0 的模块参数被冻结
推理开销	零额外延迟（并联分支可合并）	门控≈{0,1}，实际激活模块 ≤2，推理时间 +27 %
实验收益	XSum/MT 上 6.7 % 参数 ≈ 全微调 ROUGE	100-shot GLUE 平均 +2.3 %，高数据场景持平或优于最佳单模块

共同底层逻辑（数学抽象）

将多种 PELT 算子统一为可加修正项：

$$\Delta h=\sum _{i=1}^M{\alpha }_i(x)\cdot f_i(x),\sum _i{\alpha }_i(x)\le 1$$

• MAM：固定 (\alpha_i \in {0,1}) 且手工指定；
• UniPELT：令 (\alpha_i(x) = \sigma(w_i^\top x)) 可学习，实现「重要区域多分参，不重要区域零分参」的动态预算分配。

---

各个方法对比

方法	核心原理（≤1句话）	典型应用	优势	劣势	一句话类比	流行指数 (1-5)
全量微调	解冻全部权重，端到端训练	任何任务，尤其是数据充足场景	性能天花板；无需设计模块	参数量=模型×任务；存储、部署爆炸；灾难性遗忘	“把整栋房子推倒重建”	⭐⭐
BitFit	只训练bias和分类头，其余冻住	文本分类、NER等小任务	0.08 %参数即可打平Adapter；实现极简	容量上限低；对生成/复杂推理任务弱	“只调暖气阀门，不改管道”	⭐⭐⭐
Prefix Tuning	每层key/value前拼接可训练连续向量	生成式摘要、对话、翻译	深层提示→梯度直达深处；生成任务SOTA	推理要携前缀占显存；小模型<10B效果掉	“给每层发一张小抄”	⭐⭐⭐⭐
Prompt Tuning	仅在输入层插入连续token嵌入	大模型(>10B)快速任务适配	代码零改动；存储<1 MB；API黑盒可用	小模型性能塌方；序列长度受限	“在句首贴一张可撕便利贴”	⭐⭐⭐
P-Tuning	连续virtual token+轻量Encoder	中等模型NLU、抽取	收敛快；位置灵活；无需深层改动	仅限输入层；对硬序列标记弱	“用LSTM给提示炼咒”	⭐⭐⭐
P-Tuning v2	每层都插连续提示+长度搜索+CLS头	任意规模NLU/序列标注	小模型也能打平全微调；任务通用	训练超参略多；推理携深层提示	“给每层都贴LED便签”	⭐⭐⭐⭐⭐
Adapter	每层FFN后加瓶颈MLP，冻主干	多任务服务、跨语言迁移	模块化最强；即插即用；无推理前缀	推理多2×MLP延迟；需调m大小	“在暖气旁挂迷你佐料台”	⭐⭐⭐⭐
AdapterFusion	为N个Adapter加注意力融合层	多任务知识共享、连续学习	利用跨任务信息；不遗忘旧任务	推理要算全部Adapter；新增3d²/层	“让多个佐料台开圆桌会议”	⭐⭐
AdapterDrop	按梯度/层号剪掉不重要Adapter	资源受限边缘设备、大batch推理	吞吐↑1.6×；显存↓25 %；零新参	精度微降（<0.5 %）；需离线剪枝分析	“把不发言的佐料台直接踢走”	⭐⭐⭐
LoRA	低秩分解ΔW=BA，冻W₀	任意规模生成/理解；线上服务	零推理延迟；即插即拔；已工业标配	需拍秩r；对FFN无帮助；无动态预算	“给旋钮加限位铜套”	⭐⭐⭐⭐⭐
AdaLoRA	用SVD动态剪秩，重要性评分分配预算	中等规模、多任务、预算严格场景	0人工调秩；参数量↓30 %仍超LoRA	需维护奇异向量；训练代码稍复杂	“铜套自带电机，自动调宽窄”	⭐⭐⭐⭐
QLoRA	4-bit NF4权重+LoRA+分页优化器	消费级GPU微调大模型	48 GB训65 B；精度≈全调；开源即插	量化位宽太低掉点；推理需反量化	“把模型压到U盘，再插铜套”	⭐⭐⭐⭐⭐
MAM Adapter	手工固定组合：FFN并行Adapter+Prefix	文本摘要、MT	6.7 %参数≈全调；零额外延迟	组合需人工实验；无数据驱动	“手工拼乐高：佐料台+小抄”	⭐⭐
UniPELT	可学习门控动态组合LoRA+Prefix+Adapter	低数据场景、任务未知、平台统一	100样本+2.3 %；始终≥最佳单模块	推理+27 %时间；总参<10 %	“门控学拼乐高：谁有用谁上”	⭐⭐⭐⭐

流行指数说明：
⭐ 学术/小众
⭐⭐ 可用但较少
⭐⭐⭐ 社区接受度中等
⭐⭐⭐⭐ 广泛采用
⭐⭐⭐⭐⭐ 工业级标配

总的来说，像P-Tuning v2、LoRA等都是综合评估很不错的高效微调技术。如果显存资源有限可以考虑QLoRA；如果只是解决一些简单任务场景，可以考虑P-Tuning、Prompt Tuning也行。

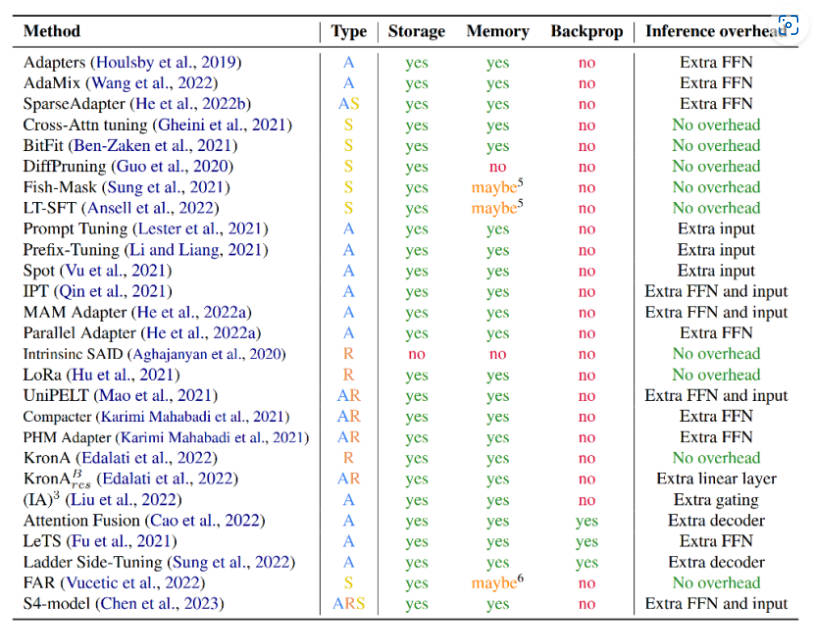
下表从参数高效方法类型、是否存储高效和内存高效、以及在减少反向传播成本和推理开销的计算高效五个维度比较了参数高效微调方法。
下表展示了各种参数高效方法的参与训练的参数量、最终模型与原始模型的改变参数（delta值）以及论文中参与评估的模型的范围（<1B、<20B、>20B）。

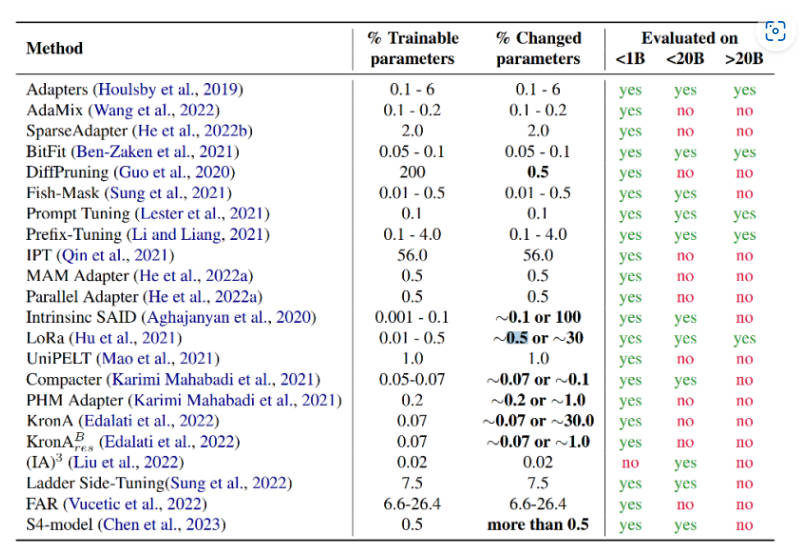
从表中可以看到，Prompt Tuning、Prefix Tuning、LoRA等少部分微调技术针对不同参数规模的模型进行过评估，同时，这几种方式也是目前应用比较多的高效微调方法。

---

总结与展望

通过本文的深入分析，我们可以清晰地看到LLM微调技术的发展脉络和未来趋势：

技术演进规律

1. 从粗放到精细：从全量微调到仅训练偏置（BitFit），再到低秩分解（LoRA），参数量从100%降至0.1%以下
2. 从静态到动态：从固定结构（Adapter）到自适应分配（AdaLoRA），再到智能组合（UniPELT）
3. 从单一到融合：从独立方法到组合策略，通过门控机制实现最优配置

选择建议

• 资源极度受限：BitFit（0.08%参数）或Prompt Tuning
• 平衡性能与效率：LoRA（工业标配）或Adapter（模块化强）
• 大模型微调：QLoRA（消费级GPU可训65B模型）
• 多任务场景：UniPELT（智能组合）或AdapterFusion（知识共享）
• 生产环境：LoRA + 量化（零推理延迟，存储友好）

未来发展方向

1. 更智能的预算分配：基于任务复杂度和数据量的自适应参数分配策略
2. 更高效的组合机制：自动发现最优的PELT方法组合，减少人工调参
3. 更细粒度的控制：在token、层、模块等不同粒度上实现精确的参数控制
4. 更实用的工程化：简化部署流程，提供开箱即用的微调框架

当前高效微调技术存在的一些问题

当前的高效微调技术很难在类似方法之间进行直接比较并评估它们的真实性能，主要的原因如下所示：

• 参数计算口径不一致：参数计算可以分为三类：可训练参数的数量、微调模型与原始模型相比改变的参数的数量、微调模型和原始模型之间差异的等级。例如，DiffPruning更新0.5%的参数，但是实际参与训练的参数量是200%。这为比较带来了困难。尽管可训练的参数量是最可靠的存储高效指标，但是也不完美。 Ladder-side Tuning使用一个单独的小网络，参数量高于LoRA或BitFit，但是因为反向传播不经过主网络，其消耗的内存反而更小。
• 缺乏模型大小的考虑：已有工作表明，大模型在微调中需要更新的参数量更小（无论是以百分比相对而论还是以绝对数量而论），因此（基）模型大小在比较不同PEFT方法时也要考虑到。
• 缺乏测量基准和评价标准：不同方法所使用的的模型/数据集组合都不一样，评价指标也不一样，难以得到有意义的结论。
• 代码实现可读性差：很多开源代码都是简单拷贝Transformer代码库，然后进行小修小补。这些拷贝也不使用git fork，难以找出改了哪里。即便是能找到，可复用性也比较差（通常指定某个Transformer版本，没有说明如何脱离已有代码库复用这些方法）。

针对以上存在的问题，研究高效微调技术时，建议按照最佳实践进行实施：

• 明确指出参数数量类型。
• 使用不同大小的模型进行评估。
• 和类似方法进行比较。
• 标准化PEFT测量基准。
• 重视代码清晰度，以最小化进行实现。

核心洞察

参数高效微调的本质是在保持模型表达能力的前提下，通过结构化的参数更新实现任务适配。无论是低秩分解、适配器插入，还是提示学习，都是在原始参数空间中寻找一个高效的子空间来承载任务特定的知识。

随着模型规模的持续增长和硬件资源的相对稀缺，PELT技术将成为LLM应用落地的关键技术路径。掌握这些方法不仅有助于降低部署成本，更能为模型的可解释性、可维护性和可扩展性提供新的思路。

---

本文涵盖了当前主流的LLM微调技术，但该领域仍在快速发展中。建议读者关注最新的研究进展，并结合具体应用场景进行技术选型。@TOC