堆与哈夫曼树详解-CSDN博客

本文链接：https://blog.csdn.net/liuerin/article/details/90813334

文章目录

6.堆（heap）

优先队列(Priority Queue)：取出元素的顺序是按照元素的优先权大小，而不是元素进入队列的先后顺序
结构上用完全二叉树实现，任何子树的根结点都是当前子树的最大值/最小值
- 如果是最大值：“最大堆”(maxheap),“大顶堆”
- 如果是最小值：“最小堆”(maxheap),“小顶堆”
堆有序：从根结点到任意节点路径上节点有序（依次变大或变小）
最大堆
最小堆

6.1创建空最大堆

确定堆的最大节点数；向堆中填充的元素列表（列表中index = 0的位置存储一个最大数值，以后做哨兵；长度为最大节点数+1）；堆中当前存放的数据数目

class heap:
    def __init__(self,maxsize):
        #存储堆元素的数组
        self.elements = []
        #堆当前元素的个数
        self.size = 0
        #堆的最大容量
        self.capacity = 0
	def create(maxsize):
		elements =  [None]*(maxsize+1)
		#0位置存储一个最大值，方便插入
		#如果是最小堆，存放float('-inf')
		elements[0] = float('inf')
		self.elements = elements
		self.size = 0
		self.capacity = maxsize

6.2 将元素插入最大堆H

由于最大堆的性质：每个节点值不小于子节点的元素值。
向列表末尾插入新元素，和当前节点的父节点比较，如果比父节点的值大，那么和父节点换位置（复杂度为 O(log N)，即树的高度）。

def insert(H,item):
	#可以通过判断capacity和size的关系得到是否已满
    if isfull(H):
        print("最大堆已满")
        return
    #把新插入值放在堆元素的最后，即为size+1的列表位置
    i=H.size + 1 
    # 与父节点元素值对比
    # 其实应该设置条件i > 0;但由于element[0]的位置放置了float('inf')，
    # 可以省略这一步
    while H.element[i//2] < item:
        H.element[i] = H.element[i//2]
        i = i//2
    H.element[i] = item

6.3 删除最大根结点

取出根结点；用堆元素列表中最后的元素填补根结点，再逐渐移动元素位置，使其满足堆的性质。移动过程：用根元素与左右两个子节点中较大的比较，如果小于这个子节点，就和其换位置。

def deleteMax(H):
	#通过判断size值判断是否为空
    if isempty(H):
        print("最大堆已空")
        return
    
    #取出根结点最大值
    maxitem = H.element[1]
    #堆最后的元素
    temp = H.element[size]
    #将元素个数-1
    H.size -= 1
    #向根结点填充,进行比较，找到真正需要填充的位置
    parent = 1
    #如果子节点存在
    while 2*parent < H.size:
        child = 2*parent
        larger = H.element[2*parent]
        #如果存在右节点，且左节点小于右节点，将右节点填充到当前父节点
        if child !=H.size and H.element[child ] < H.element[child +1]:
            larger = H.element[child +1]
            child += 1
        #如果子节点值更大，将子节点移动到父节点位置
        if larger > temp:
            H.element[parent] = H.element[child]
            parent = child
        else:
            break
    H.element[parent] = item
    return maxitem

6.4最大堆的建立

将已存在的N个元素按最大堆的要求存放在一个一维数组中。

通过插入操作，将元素一一插到空堆中，复杂度为O(nlogn)
将N个元素按顺序存入，先满足完全二叉树；接着调整个节点位置，以满足最大堆的有序特性。

例如：元素列表[79,66,43,83,30,87,38,55,91,72,49,9],先满足完全二叉树

将第一个有子节点的父节点作为根结点，其所在的子树（最多有三个节点，最少有两个节点），调整为堆结构；即9和87的子树，堆结构仍然为[87,9]
再依次将第二个有子节点的父节点作为根结点，将这个子树调整为堆结构；即30,72,49,堆结构为[72,30,49]；将倒数第一层和倒数第二层调整成堆。

开始调整倒数第三层，即先调整43的节点，后调整66的节点。想象成删除最大值的操作：刚删除这个根结点，再用末尾元素43补充到根结点的位置，与其左右节点进行比较，调整这个堆（删除函数中的部分代码）。

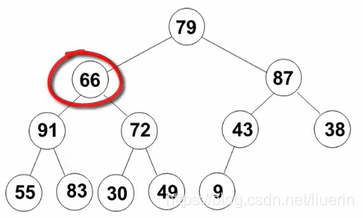
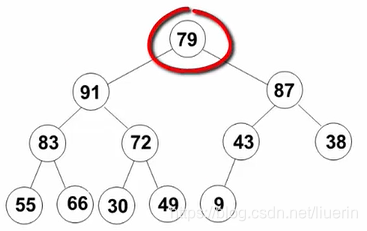
调整根节点79

7.哈夫曼树(Huffman Tree)与哈夫曼编码

举例
根据百分制的考试成绩的不同区间，转换为五分制的成绩，生成一个判定树。叶节点是分类的结果。

由于成绩区间有概率分布，平均查找次数 $ASL=\sum\text{成绩为某区间的概率}*\text{这个分类结果的查找次数}$ 。
可以根据不同的查找频率构造更有效的搜索树，即频率越大，查找次数越小。

概念

带权路径长度(WPL)：设二叉树有n个叶节点，每个叶节点带有权值 $w_k$ ，从根结点到每个叶节点的长度为 $I_k$ ，则每个叶节点的带权路径长度之和是： $\sum_{k=1}^n w_kl_k$
最优二叉树或哈夫曼树：WPL最小的二叉树

7.1 哈夫曼的构造

每次把权值最小的两颗二叉树合并，将其作为一个子树，这个子树的权值是两个最小权值之和。相当于在构建最小堆。
例如：[1,2,3,4,5]构成最小堆，取出两个权值最小的节点1,2，构成一个子树，权值为3，插到最小堆中，构成[3,3,4,5],再依次构建，最后构成

class Node():
    def __init__(self,weight=0):
        self.weight = weight
        self.left = None
        self.right = None
#最终返回的是huffman树，具有树结构。
#而最小堆中，elements中只考虑当前Node.weight,不考虑node的左右子节点
def createHuffman(MinHeap H):
    #当前节点按权值调成最小堆（存储在堆的elements中）
    BuildMinHeap(H)
    i=1
    while i < H.size:
        #构建新的节点
        T = Node()
        #节点的左右分别为当前堆的第一小和第二小
        #deletemin函数是返回堆中最小值，并且会调整最小堆
        T.left = DeleteMin(H)
        T.right = DeleteMin(H)
        #新节点的权值是第一小和第二小的权值之和
        T.weight = T.left.weight + T.right.weight
        #将新节点插入最小堆
        Insert(H,T)
    T = deletemin(H)
    return T

7.2 哈夫曼树的特点

没有度为1的节点
如果有n个叶节点，树的总节点为2n-1
哈夫曼树左右子树交换后仍然是哈夫曼树（只要每个叶节点到根结点的路径长度不变即可）
同一组权值，可能存在不同构的两颗哈夫曼树，但WPL是相同的

7.3哈夫曼编码

举例：如果给定一段字符串，有[a,u,x,z]四个字符，对字符编码，使得存储空间最少。可以不等长编码：出现频率高的字符编码短些，频率低的字符编码长些

前缀码：任何字符的编码都不是另一字符编码的前缀（可以无二义的编码）
二叉树编码：用二叉树表示编码。当所有结果都在叶节点上时，就不会出现一个字符的编码是另一个字符的前缀。当一个字符是另外一个字符的父节点时，才会出现前缀码

用等长编码：分别编码[00,01,10,11]
haffuman编码：按字母的频率构造haffuman树。分别编码[0,10,110,111]

8. 集合

例子：有n台电脑，某些电脑间两两相连，是不是所有的电脑都连在了一起。

集合并、查元素属于哪个集合

8.1集合的表示

可以用树表示集合，每个节点代表一个集合元素；
子元素指向父元素；
如果节点间最终指向的父元素相同，那么这些节点在同一个集合中
集合的并，相当于将两个树根结点的其中一个指向另一个；但为了降低树的高度，把元素少的树的根结点指向元素多的树的根结点
树用列表来表示，存储的是所有的节点。

#定义节点
class Node():
	def __init__(self, data):
		self.data = data
		#parent为负数时，代表没有根结点，且以这个节点为根的树中总的节点数为-parent；
		#当parent为正数时，表示这个节点的父节点在列表中存储的index
		self.Parent = -1

例如：对于三个集合

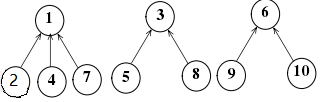
用列表存储各个节点，如下图所示

8.2集合的查找

找到根结点的根结点

def find( S ,  x):
	"""S是当前所有集合的列表，x是某元素值，找到x所在的集合"""
	i = 0
	for node  in S:
		if node.data == x:
			break
		else:
			i+=1
	if i >= len(S):
		#没找到x
		return -1
	while S[i].parent >= 0:
		i = S[i].parent
	return i

8.3集合的并

例：把上面的3根结点集合与1根结点集合合并，由于3根结点集合只有3个节点，1根结点集合有4个节点，将3根结点的父节点指向1根结点。

列表变成

def union(s, x1, x2):
	"""将x1和x2所在的集合合并，即改变其中一个根结点的parent"""
	root1 = find(S,x1)
	root2 = find(S,x2)
	if root1 != root2:
		#把集合数目小的根结点指向集合数组大的根结点
		if -S[root1].parent < -S[root2].parent:
			#更新这个集合的总数目
			S[root2].parent +=  S[root1].parent
			S[root1].parent = root2
		else:
			S[root1].parent +=  S[root2].parent
			S[root2].parent = root1