[LeetCode解题报告] 1976. 到达目的地的方案数
一、 题目
1. 题目描述
你在一个城市里,城市由 n 个路口组成,路口编号为 0 到 n - 1 ,某些路口之间有 双向 道路。输入保证你可以从任意路口出发到达其他任意路口,且任意两个路口之间最多有一条路。
给你一个整数 n 和二维整数数组 roads ,其中 roads[i] = [ui, vi, timei] 表示在路口 ui 和 vi 之间有一条需要花费 timei 时间才能通过的道路。你想知道花费 最少时间 从路口 0 出发到达路口 n - 1 的方案数。
请返回花费 最少时间 到达目的地的 路径数目 。由于答案可能很大,将结果对 109 + 7 取余 后返回。
示例 1:
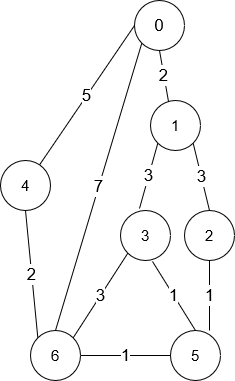
输入:n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]] 输出:4 解释:从路口 0 出发到路口 6 花费的最少时间是 7 分钟。 四条花费 7 分钟的路径分别为: - 0 ➝ 6 - 0 ➝ 4 ➝ 6 - 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6 - 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
示例 2:
输入:n = 2, roads = [[1,0,10]] 输出:1 解释:只有一条从路口 0 到路口 1 的路,花费 10 分钟。
提示:
1 <= n <= 200n - 1 <= roads.length <= n * (n - 1) / 2roads[i].length == 30 <= ui, vi <= n - 11 <= timei <= 109ui != vi- 任意两个路口之间至多有一条路。
- 从任意路口出发,你能够到达其他任意路口。
Related Topics
- 图
- 拓扑排序
- 动态规划
- 最短路
- 👍 32
- 👎 0
2. 原题链接
链接: 1976. 到达目的地的方案数
二、 解题报告
1. 思路分析
- 思路一,dp,来自英雄哥,dp[i][j]表示从经过i个节点到达j的最短时间,那么dp[i][j]一定从dp[i-1][k]转移而来,找j的临近节点即可。
- 思路二,最短路+dp,来自官方题解。
- 先找到从起始0到每个点的最短时间dist[i],
- 然后重新建图,节点还是原图节点;边满足如下:找到u,v,使dist[v]-dist[u] == w[u][v],这意味着从u到v这条边是一条最短路上的路线,建立边。
- 在新的图上,任意一条路线都是到终点的最短路,直接dp即可。
- 由于是图,需要以拓扑排序的顺序进行DP,这也是今天最大的思路收获:对于状态dp[v]来说,状态需要从{dp[u]}转移而来,那么需要保证在这个有向图的拓扑排序里,任意u都在v之前。
- 在
思路二的基础上,最后的DP其实可以直接记忆化搜索,代码也好写。
2. 复杂度分析
- 对于思路一来说,时间复杂度为O(n2m),m是一个点最多边的数量,根据题意 n - 1,所以最坏应该是O(n3)
- 最短路算法今天学了Dijkstra和FLoyd,分别是O(n2)和O(n3),其中Dijkstra可以用优先队列优化成O(nlog2n)
3. 代码实现
思路一 dp。2512 ms
class Solution:
def countPaths(self, n: int, roads: List[List[int]]) -> int:
mod = 10**9+7
graph = [[0]*n for _ in range(n)]
graph = collections.defaultdict(dict)
for u,v,w in roads:
graph[u][v] = w
graph[v][u] = w
dp = [[1e13]*n for _ in range(n)] # dp[i][j]表示从经过i个节点到达j的最短时间,那么dp[i][j]一定从dp[i-1][k]转移而来
cnt = [[0]*n for _ in range(n)] # cnt[i][j]表示从经过i个节点到达j的最短时间的方案数
dp[0][0] = 0 # 起点到起点不需要花时间
cnt[0][0] = 1 # 起点到起点只有一种方案
for i in range(1,n):
for j in range(1,n):
for v,w in graph[j].items(): # dp[i][j] 从dp[i-1][v]转移而来,v必是j的邻居
vt = dp[i-1][v] + w # 如果从v转移来,要花的时间
if dp[i][j] > vt: # 如果时间小,则更新,只能从v转移来
dp[i][j] = vt
cnt[i][j] = cnt[i-1][v]
elif dp[i][j] == vt: # 如果时间相等,则可以转移来,方案数累计
cnt[i][j] = (cnt[i][j] +cnt[i-1][v])%mod
else: # 时间还不如当前,则不转移
pass
min_t = min([dp[i][n-1] for i in range(n)])
ans = 0
for i in range(n):
if dp[i][n-1]==min_t:
ans = (ans + cnt[i][n-1]) % mod
return ans
思路二 自己写朴素BFS最短路+拓扑排序dp。72 ms
class Solution:
def countPaths(self, n: int, roads: List[List[int]]) -> int:
mod = 10**9+7
graph = collections.defaultdict(dict)
for u,v,w in roads:
graph[u][v] = w
graph[v][u] = w
# 先算每个节点最短路,visited储存从0开始到每个节点的最短时间
q = deque([0])
visited = {0:0} # 0的最短时间是0
while q:
u = q.popleft()
x = visited[u]
for v,w in graph[u].items():
if v not in visited or x + w < visited[v]: # 如果新节点没遍历过,或者之前的路不够短,遍历他
visited[v] = x + w
q.append(v)
# 重新建图,如果到v的最短路长度-到u的最短路长度恰好是w[u][v],则建立边,最终路径只能沿着这些边走
# 这是一个DAG,可以拓扑排序后DP
graph2 = collections.defaultdict(list) # DAG
graph3 = collections.defaultdict(list) # 反图,记v的邻居
indegree = [0]*n
for u,v,w in roads:
if visited[v]-visited[u] == w:
graph2[u].append(v)
graph3[v].append(u)
indegree[v] += 1
elif visited[u]-visited[v] == w:
graph2[v].append(u)
graph3[u].append(v)
indegree[u] += 1
q2 = deque([i for i in indegree if i == 0])
sorted_u = []
while q2:
u = q2.popleft()
sorted_u.append(u)
for v in graph2[u]:
indegree[v] -= 1
if indegree[v] == 0:
q2.append(v)
dp = [0]*n # dp[i] 储存从起点到i有多少种走法
dp[0] = 1
for i in range(1,len(sorted_u)):
u = sorted_u[i]
dp[u] = 0
for v in graph3[u]:
dp[u] = (dp[u]+dp[v])%mod
return dp[n-1]
思路三 抄官方Dijkstra+记忆化搜索。168 ms
class Solution:
def countPaths(self, n: int, roads: List[List[int]]) -> int:
mod = 10**9+7
graph = collections.defaultdict(dict)
for u,v,w in roads:
graph[u][v] = w
graph[v][u] = w
dist = [[float("inf")] * n for _ in range(n)]
for i in range(n):
dist[i][i] = 0
for x, y, z in roads:
dist[x][y] = dist[y][x] = z
# Dijkstra 算法求解最短路
# 完成后,dist[0][i] 即为正文部分的 dist[i]
seen = set()
for _ in range(n - 1):
u = None
for i in range(n):
if i not in seen and (not u or dist[0][i] < dist[0][u]):
u = i
seen.add(u)
for i in range(n):
dist[0][i] = min(dist[0][i], dist[0][u] + dist[u][i])
# 重新建图,如果到v的最短路长度-到u的最短路长度恰好是w[u][v],则建立边,最终路径只能沿着这些边走
# 这是一个DAG,可以拓扑排序后DP
graph2 = collections.defaultdict(list) # DAG
graph3 = collections.defaultdict(list) # 反图,记v的邻居
indegree = [0]*n
for u,v,w in roads:
if dist[0][v]-dist[0][u] == w:
graph2[u].append(v)
graph3[v].append(u)
indegree[v] += 1
elif dist[0][u]-dist[0][v] == w:
graph2[v].append(u)
graph3[u].append(v)
indegree[u] += 1
# 好像dfs更好写
@cache
def dfs(u):
if u == 0:
return 1
ret = 0
for v in graph3[u]:
ret = (ret+dfs(v))%mod
return ret
return dfs(n-1)
思路三 自己封装Dijkstra+记忆化搜索。84 ms
class Solution:
def countPaths(self, n: int, roads: List[List[int]]) -> int:
mod = 10**9+7
graph = collections.defaultdict(dict)
for u,v,w in roads:
graph[u][v] = w
graph[v][u] = w
def dijkstra(graph,start,size):
dist = [float("inf")] * size # 初始化距离数组
dist[start] = 0 # 原点到自己是0
visited = set([start]) # 访问过原点了
for v,w in graph[start].items(): # 找到所有原点的邻居,更新他们的dist
dist[v] = w
for _ in range(size):
mid = float("inf")
u = 0
for i in range(size):
if i not in visited and dist[i] < mid: # 找到距离原点最近的点,用它给别的节点做松弛
mid = dist[i]
u = i
visited.add(u)
for v,w in graph[u].items():
dist[v] = min(dist[v],dist[u]+w)
return dist
dist = dijkstra(graph,0,n)
# 重新建图,如果到v的最短路长度-到u的最短路长度恰好是w[u][v],则建立边,最终路径只能沿着这些边走
# 这是一个DAG,可以拓扑排序后DP
graph3 = collections.defaultdict(list) # 反图,记v的邻居
for u,v,w in roads:
if dist[v]-dist[u] == w:
graph3[v].append(u)
elif dist[u]-dist[v] == w:
graph3[u].append(v)
@cache
def dfs(u):
if u == 0:
return 1
ret = 0
for v in graph3[u]:
ret = (ret+dfs(v))%mod
return ret
return dfs(n-1)
思路三 优先队列优化Dijkstra+记忆化搜索。68 ms
class Solution:
def countPaths(self, n: int, roads: List[List[int]]) -> int:
mod = 10**9+7
graph = collections.defaultdict(dict)
for u,v,w in roads:
graph[u][v] = w
graph[v][u] = w
def dijkstra(graph,start,size):
from queue import PriorityQueue
dist = [float("inf")] * size # 初始化距离数组
dist[start] = 0 # 原点到自己是0
visited = set([start]) # 访问过原点了
q = PriorityQueue()
for v,w in graph[start].items(): # 找到所有原点的邻居,更新他们的dist
dist[v] = w
q.put((w,v)) # 权放前边,注意是put
while not q.empty():
x,u = q.get() # 用u给别的节点做松弛,注意是get
if u in visited:
continue
visited.add(u)
for v,w in graph[u].items():
new_dist = dist[u]+w
if new_dist < dist[v]:
dist[v] = new_dist
if v not in visited:
q.put((new_dist,v))
return dist
dist = dijkstra(graph,0,n)
# 重新建图,如果到v的最短路长度-到u的最短路长度恰好是w[u][v],则建立边,最终路径只能沿着这些边走
# 这是一个DAG,可以拓扑排序后DP
graph3 = collections.defaultdict(list) # 反图,记v的邻居
for u,v,w in roads:
if dist[v]-dist[u] == w:
graph3[v].append(u)
elif dist[u]-dist[v] == w:
graph3[u].append(v)
@cache
def dfs(u):
if u == 0:
return 1
ret = 0
for v in graph3[u]:
ret = (ret+dfs(v))%mod
return ret
return dfs(n-1)
思路三 封装Floyd+记忆化搜索。9952 ms
这里基本是卡过了,放到这里留个模板
class Solution:
def countPaths(self, n: int, roads: List[List[int]]) -> int:
mod = 10**9+7
graph = collections.defaultdict(dict)
for u,v,w in roads:
graph[u][v] = w
graph[v][u] = w
def floyd(graph,size):
""" floyd可以求出这个图中任意两点之间的最短距离,本质是遍历所有k,用经过k的方式代替原先的dist[i][j],时间复杂度n^3
"""
dist = [[float("inf")] * size for _ in range(size)] # 初始化距离数组
for i in range(size): # 任意点到自己是0
dist[i][i] = 0
for u,vs in graph.items():
for v,w in vs.items():
dist[u][v] = w
dist[v][u] = w
for k in range(size): # 中间点,也就是经过的点,如果需要记path,则发现小就记k
for u in range(size): # 左短点
for v in range(size): # 右端点
dist[u][v] = min(dist[u][v],dist[u][k]+dist[k][v])
return dist
dist = floyd(graph,n)[0]
# 重新建图,如果到v的最短路长度-到u的最短路长度恰好是w[u][v],则建立边,最终路径只能沿着这些边走
# 这是一个DAG,可以拓扑排序后DP
graph3 = collections.defaultdict(list) # 反图,记v的邻居
for u,v,w in roads:
if dist[v]-dist[u] == w:
graph3[v].append(u)
elif dist[u]-dist[v] == w:
graph3[u].append(v)
@cache
def dfs(u):
if u == 0:
return 1
ret = 0
for v in graph3[u]:
ret = (ret+dfs(v))%mod
return ret
return dfs(n-1)
三、 本题小结
- 迪杰斯特拉算法 可以从O(n2)优化成O(nlog2n)*。
- dijkstra只能处理单元最短路,floyd可以处理全部。
- dijkstra不能处理负权图,而floyed可以。
























 608
608











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








