1 三次Beizer曲线方程介绍
Beizer曲线的一些特性这里不再赘述,大家可以去网上查看一些资料,很详细。最近用到轮廓拟合,所以用三次Beizer曲线效果还可以,有插值和近似拟合(插值就是曲线过点,近似拟合则不过点),就学习了一下。我是做的Beizer曲线插值,插值和近视拟合无非就是控制点选取不一样。
Beizer总方程为
∑PiKni(t)
(1),
三次Beizer曲线方程:
Bn(t)=P0(1−t)3+3P1t(1−t)2+3P2t2(1−t)+P3t3,tϵ[0,1]
(2),
这里的
P1
和
P2
就是所谓的控制点A、B点。关于控制点AB的求法很多种,我是采用参数设定法构造控制点,思路我是参考百度文库一篇文章,“确定控制点文章链接”。文章写的很详细,对于闭合轮廓的话就想象成一个循环,第0个点的前两个点为n-1和n-2,第n-1个点的后两个点为0和1,文章很好理解。对于参数a和b,通常都是0.25,但我看别人论文中有a=0.125,b=0.05,拟合出来的效果很接近真实曲线,所以我也是采用这个参数。
2 代码实现
上述讲了三次Beizer曲线方程,用在轮廓拟合中怎么实现呢。当然,你先得找到轮廓中的特征点,然后根据两个相邻的特征点拟合成一段三次Beizer曲线,控制点AB是借助周围几个点得到的。思路大概就是这样的。下面讲一下具体步骤。
###2.1 得到控制点AB
控制点AB方程在刚才那篇百度文科文章中有,所以直接根据那个方程来编写代码,下面是我求控制点AB的代码,很简单,大家有需要的可以参考。
//求得控制点AB
void ControlAB(double *Xi,double *Yi, double *Ai_x,double *Ai_y, double *Bi_x,double *Bi_y,int n, double a, double b,int boundType)
{
if(boundType==1)
{
Ai_x[0]=Xi[0]+(Xi[1]-Xi[n-1])*a;
Ai_y[0]=Yi[0]+(Yi[1]-Yi[n-1])*a;
Bi_x[n-2]=Xi[n-1]-(Xi[0]-Xi[n-2])*b;
Bi_y[n-2]=Yi[n-1]-(Yi[0]-Yi[n-2])*b;
Ai_x[n-1]=Xi[n-1]+(Xi[0]-Xi[n-2])*a;
Ai_y[n-1]=Yi[n-1]+(Yi[0]-Yi[n-2])*a;
Bi_x[n-1]=Xi[0]-(Xi[1]-Xi[n-1])*b;
Bi_y[n-1]=Yi[0]-(Yi[1]-Yi[n-1])*b;
}
for(int i=1;i<n-1;i++)
{
Ai_x[i]=Xi[i]+(Xi[i+1]-Xi[i-1])*a;
Ai_y[i]=Yi[i]+(Yi[i+1]-Yi[i-1])*a;
}
for(int i=0;i<n-2;i++)
{
Bi_x[i]=Xi[i+1]-(Xi[i+2]-Xi[i])*b;
Bi_y[i]=Yi[i+1]-(Yi[i+2]-Yi[i])*b;
}
}代码注意:代码不要瞎贴,这里有些自定义数组,Xi、Yi是点的x、y。
###2.2 拟合曲线生成与绘制
求得AB控制点,可以将
P1
、
P2
、A和B代入方程(2)中,得到
P1
和
P2
中间的一段三次Beizer曲线方程,就拟合出来了。这时需要看到效果。我用的是C++的MFC画出来的曲线,当然也可以Python,Python一搜有很多例子,网上可以荡到的。我画二维曲线用的是MFC,大家可以参考我的博客“MFC绘制二维曲线”,给个我实验拟合出来的闭合轮廓,其中参数a=0.125,b=0.05。
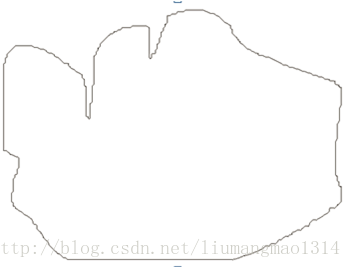

可以看到,拟合效果还是不错的。图中的小黑点是我给的特征点,MFC画出来就是这个样子。
3 总结
三次Beizer曲线拟合算法还是很简单的,主要是控制点的选取,还有最关键的特征点选取。特征点是最基本的。当然Beizer也有一些不足之处,对于非闭合轮廓的情况拟合情况不是很理想,这就需要其他的曲线拟合,我会再发一篇B样条曲线拟合算法的。






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








