动态规划之树形DP

树形DP

何为树形DP

树形DP是指在“树”这种数据结构上进行的动态规划：给出一颗树，要求以最少的代价（或取得最大收益）完成给定的操作。通常这类问题规模比较大，枚举算法效率低，无法胜任，贪心算法不能求得最优解，因此需要用动态规划进行求解。

在树上做动态规划显得非常合适，因为树本身有“子结构”性质（树和子树），具有递归性，符合DP性质。相比线性DP，树形DP的状态转移方程更加直观。

树形动态规划（Tree DP）是一种动态规划算法，在处理树状结构（例如树、森林、有向无环图等）上的问题时非常常见和有效。树形动态规划通过将问题拆解为子问题，并利用子问题的解来求解更大规模的问题。

在树形动态规划中，我们需要定义一个适合的状态和状态转移方程。一般来说，状态可以定义为以当前节点为根的子树的某种性质，例如最大路径和、最长路径长度、最大权值和等等。而状态转移方程则描述了如何由子节点的状态计算当前节点的状态。

树形动态规划的典型做法是使用深度优先搜索（DFS）遍历整个树，在遍历过程中进行状态的计算和更新。通过递归地计算子节点的状态，并将其传递给父节点，可以得到整个树的最终状态。

在实现树形动态规划时，需要注意避免重复计算，可以使用记忆化搜索或者自底向上的方式进行计算。此外，还要注意选择合适的遍历顺序，以保证子问题的状态在计算当前节点状态时已经求解完毕。

总而言之，树形动态规划是一种针对树状结构问题的动态规划算法，通过拆解问题为子问题，并利用子问题的解求解更大规模的问题。它在解决树相关的问题时具有重要的应用价值。

树形DP例题

HDU-1520 Anniversary party

HDU-1520 Anniversary party

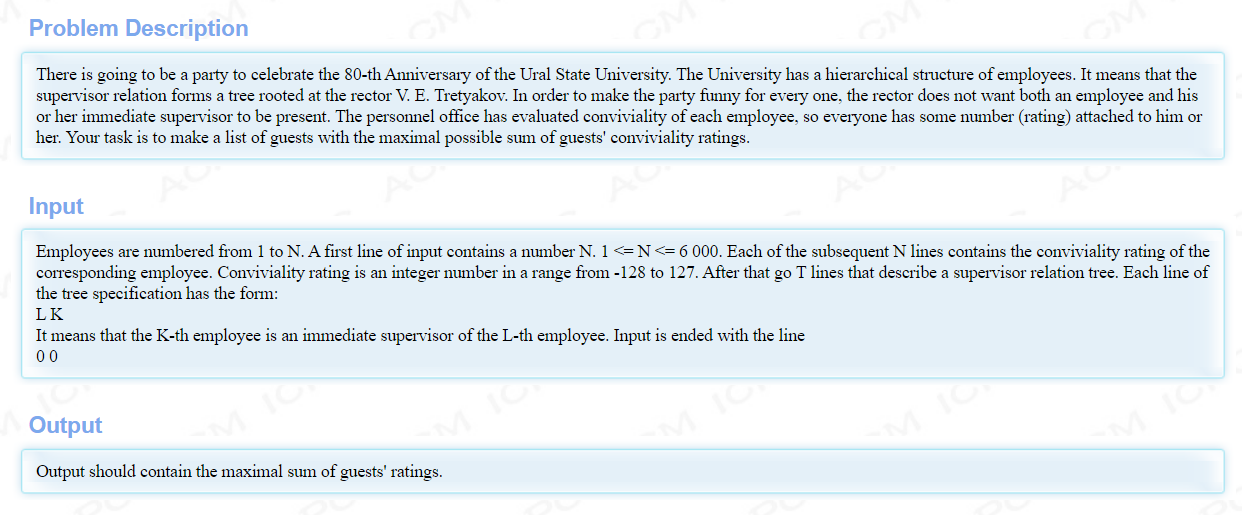
题目大意：

邀请员工参加party,但是为了避免员工和直属上司发生尴尬，规定员工和直属上司不能同时出席。

也就是每个人代表树中一个结点，每个结点拥有一个权值，相邻的父结点和子结点只能选择一个，问如何取才能使总权值之和最大。

员工编号从1到N。第一行输入包含数字N。1 < = N < = 6000。随后的N行中的每一行都包含相应员工的愉快度评级。欢乐评级是一个介于-128到127之间的整数。然后是描述主管关系树的T行。树规范的每一行都具有以下形式: L K 这意味着第K个员工是第L个员工的直接主管。输入以一行结束 0 0

解题思路：

根据DP的解题思路，定义状态为：

$dp[i][0]$，表示不选择当前结点时候的最优解

$dp[i][1]$，表示选择当前结点时候的最优解

其中状态转移方程分为下面两种情况：

1. 不选择当前结点，则子结点可选可不选，取其中的最大值即可，也就是$dp[u][0]+=max(dp[son][0],dp[son][1])$
2. 选择当前结点，则其子结点不能选，$dp[u][1]+=dp[son][0]$

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 6010;
vector<int>tree[maxn];
int dp[maxn][2], father[maxn], value[maxn];
void dfs(int u) {
   
   
    dp[u][0] = 0; // 不参加party
    dp[u][1] = value[u]; // 参加party
    for(int i = 0; i < tree[u].size(); i++) {
   
   
        int son = tree[u][i];
        dfs(son); // 深搜子结点
        dp[u][0] += max(dp[son][0], dp[son][1]); // 父结点不选，子结点可选可不选
        dp[u