题目概述
给定三角形顶点坐标,以三角形每条边向外各做一正方形,将任意两个正方形上有公共点的边的另一个点连接,取所连成线段中点,向公共点(三角形顶点)做直线,如此三条直线会交于一点,求该点坐标
三角形不会退化为线段
时限
1000ms/3000ms
输入
第一行正整数times,其后times组数据,每组数据共三行,每行两个浮点数,描述一个顶点坐标
限制
没有限制
输出
每行两个保留四位小数的浮点数,为所求点坐标
样例输入
2
0.0 0.0
9.0 12.0
14.0 0.0
3.0 4.0
13.0 19.0
2.0 -10.0
样例输出
9.0000 3.7500
-48.0400 23.3600
讨论
计算几何,解决之只需要计算几何的知识,证明的话,用计算几何也能足够,不过还是算入解析几何吧,因为求的这个点其实就是垂心,三角形三条高的交点,初中的话证明这个应该是相当简单,额下面用计算几何的一点知识证明,能简单不少
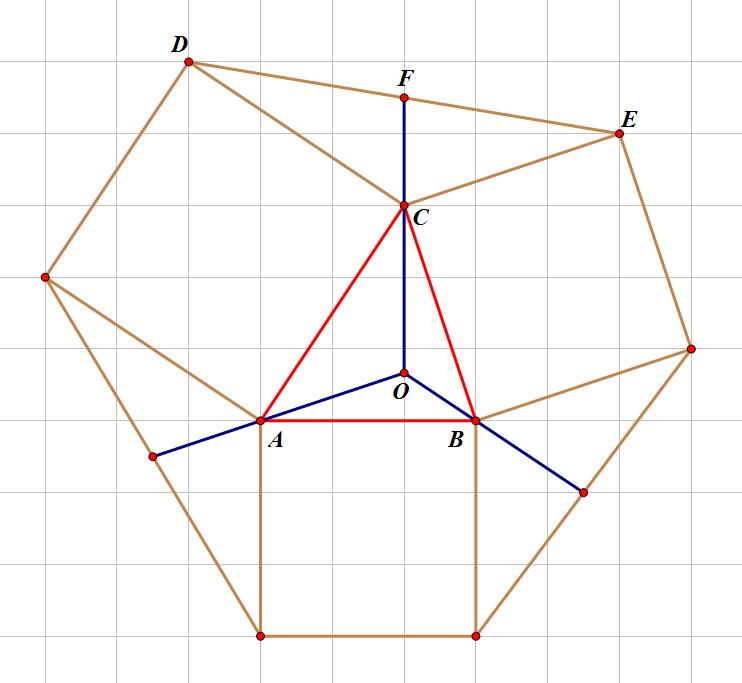
已知点
A(xA,yA),B(xB,yB),C(xC,yC)
由计算几何知识易得点
D(xC−yC+yA,yC+xC−xA),E(xC+yC−yB,yC−xC+xB)
得
DE
中点
F(xC+12yA−12yB,yC−12xA+12xB)
得
FC−→−=(−12yA+12yB,12xA−12xB)
同时算出
AB−→−=(xB−xA,yB−yA)
经计算
FC−→−⋅AB−→−=0
知
FC⊥AB
同理可证另外两条线
故其交点
O
<script id="MathJax-Element-1342" type="math/tex">O</script>为三角形垂心
再往下,利用方向向量的思想求出两条高线上的另外一个点,然后求出高线交点,返回结果
从实现层面上,只需要注意,由于可能会出现-0.0000的情况,因此结果需要+EPS后输出
题解状态
180K,0MS,C++,1085B
题解代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
#define INF 0x3f3f3f3f
#define MAXN 1003
#define memset0(a) memset(a,0,sizeof(a))
#define EPS 1e-8
double xp(double x1, double y1, double x2, double y2, double x3, double y3)
{
return (x1 - x2)*(y3 - y2) - (y1 - y2)*(x3 - x2);
}
void point_of_intersection(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4, double &poix, double &poiy)
{
double Sabc = xp(x3, y3, x1, y1, x2, y2), Sabd = xp(x4, y4, x1, y1, x2, y2);
poix = (Sabc*x4 - Sabd*x3) / (Sabc - Sabd);
poiy = (Sabc*y4 - Sabd*y3) / (Sabc - Sabd);
}
void fun()
{
double x1, y1, x2, y2, x3, y3;//三个顶点的坐标
scanf("%lf%lf%lf%lf%lf%lf", &x1, &y1, &x2, &y2, &x3, &y3);//input
double poix, poiy;
point_of_intersection(x1, y1, y2 - y3 + x1, x3 - x2 + y1, x3, y3, y2 - y1 + x3, x1 - x2 + y3, poix, poiy);//利用方向向量的思想直接得到高线上另外的点的坐标 这个思想在前面用过很多次了 但是不好用文字解释 已知正方形对角线上两点求另外两点也是这个思想
printf("%.4lf %.4lf\n", poix + EPS, poiy + EPS);//output
}
int main(void)
{
//freopen("vs_cin.txt", "r", stdin);
//freopen("vs_cout.txt", "w", stdout);
int times;
scanf("%d", ×);//input
while (times--) {
fun();
}
}EOF
























 1053
1053

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








