决策树简介及代码实现

一、决策树基础：

决策树是一种用于对实例进行分类的树形结构

决策树，由节点和有向边组成

节点的类型有两种：内部节点和叶子节点。其中，内部节点表示一个特征或属性的测试条件（用于分开具有不同特性的记录），叶子节点表示一个分类。

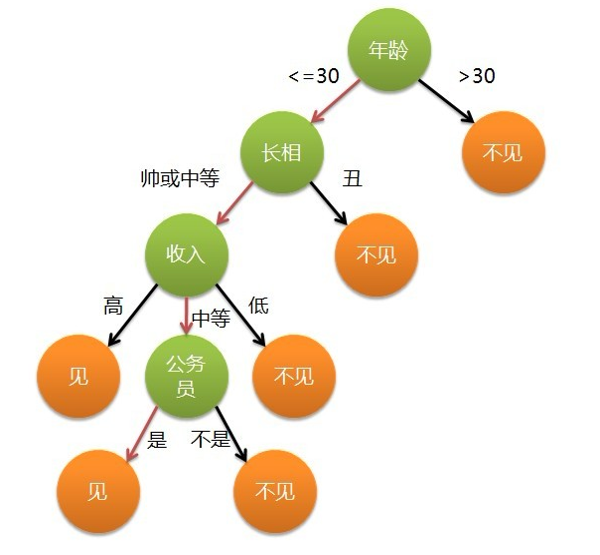
图是女孩对是否与男生见面的决策过程

橙色的为叶子节点，绿色的为内部节点

二、算法思想

决策树就好像是if-else结构一样，它的结果就是你要生成这个一个可以从根开始不断判断选择到叶子节点的树，但是，这里的if-else必然不是我们人为去设置，我们要做的是提供一种方法，计算机可以根据这种方法得到我们所需要的决策树。

  这个方法的重点就在于如何从这么多的特征中选择出有价值的，并且按照最好的顺序由根到叶选择。完成了这个我们也就可以递归构造一个决策树了

三、ID3算法

ID3算法是用信息增益来判断当前节点应

用什么特征来构建决策树。信息增益越大，则越

适合用来分类。（如下介绍）

四、信息论基础

熵：熵度量了事物的不确定性，越不确定的事物，它的熵就越大。具体的，随机变量X的熵的表达式如下：

             

其中n代表X的n种不同的离散取值。而pi代表了X取值为i的概率，log为以2为底的对数

    举个例子，比如X有2个可能的取值，而这两个取值各为1/2时

               

条件熵的表达式H(X|Y)

  条件熵,它度量了我们的X在知道Y以后剩下的不确定性。

  表达式如下：

         

信息增益：

   信息增益是特征选择中的一个重要指标，它定义为一个特征能够为分类系统带来多少信息，带来的信息越多，该特征越重要

              H(X) - H(X|Y)

举个例子：

   比如我们有15个样本D，输出为0或者1。其中有9个输出为0， 6个输出为1。 样本中有个特征A，取值为A1，A2和A3。在取值为A1的样本的输出中，有3个输出为1， 2个输出为0，取值为A2的样本输出中,2个输出为1,3个输出为0， 在取值为A3的样本中，4个输出为1，1个输出为0.

      

五、解析代码

导入模块

#coding=utf-8
from math import log
import operator

创建简单的数据集：

def createDataSet():
    dataSet = [[1,1,0,'fight'],[1,0,1,'fight'],[1,0,1,'fight'],
               [1,0,1,'fight'],[0,0,1,'run'],[0,1,0,'fight'],
               [0,1,1,'run']]
    lables = ['weapon','bullet','blood']
    return dataSet,lables

①数据是由列表元素组成的列表，而且所有的列表元素都要具有相同的数据长度
② 数据的最后一列或者每个实例的最后一个元素是当前实例的类别标签

字段说明 [1,1,0,'fight']

计算数据集的香农熵，分两步，第一步计算  频率，第二部根据公式计算香农熵：

def calcShannonEnt(dataSet):#输入训练数据集  
    numEntries = len(dataSet)#计算训练数据集中样例的数量  
    labelCounts = {}  
    for featVec in dataSet:  
        currentLabel = featVec[-1]#获取数据集的标签  
        if currentLabel not in labelCounts.keys():  
            labelCounts[currentLabel]=0  
        labelCounts[currentLabel]+=1 #当前标签实例数+1  
        shannonEnt = 0.0  
        for key in labelCounts:  
            prob = float(labelCounts[key])/numEntries  
            shannonEnt -= prob *log(prob,2)#计算信息熵  
    return shannonEnt

按照给定特征划分数据集

  划分数据集，将满足X[axis]==value的值都划分到一起，返回一个划分好的集合（不包括用来划分的axis属性，因为不需要）

def splitDataSet(dataSet,axis,value):#划分属性，获得去掉axis位置的属性value剩下的样本  
    retDataSet = []  
    for featVec in dataSet:  
        if featVec[axis] == value :  
            reduceFeatVec = featVec[:axis]  
            reduceFeatVec.extend(featVec[axis+1:])#extend()方法接受一个列表作为参数，并将该参数的每个元素都添加到原有的列表中  
            retDataSet.append(reduceFeatVec)#append()方法向列表的尾部添加一个新的元素，只接受一个参数。  
    return retDataSet  

选择最好的数据集划分方式：

   选择最好的属性进行划分，思路很简单就是对每个属性都划分一下，看哪个好。

def chooseBestFeatureToSplit(dataSet):#选择最好的特征  
    numFeatures = len(dataSet[0])-1  
    baseEntropy = calcShannonEnt(dataSet)  
    bestInfoGain = 0.0; bestFeature = -1  
    for i in range(numFeatures):  
        featList = [example[i] for example in dataSet]  
        uniqueVals = set(featList)#将特征值放到一个集合中，消除重复的特征值  
        newEntropy = 0.0  
        for value in uniqueVals:  
            subDataSet = splitDataSet(dataSet,i,value)  
            prob = len(subDataSet)/float(len(dataSet))  
            newEntropy += prob * calcShannonEnt(subDataSet)  
        infoGain = baseEntropy - newEntropy#计算信息增益  
        if(infoGain>bestInfoGain):  
            bestInfoGain = infoGain  
            bestFeature = i  
    return bestFeature  

递归构建决策树

基于递归构建决策树。这里的label是对于分类特征的名字

def createTree(dataSet,labels):#构建分类树  
    classList = [example[-1] for example in dataSet]#获得类别列  
    if classList.count(classList[0]) == len(classList):#所有样本属于同一类别  
        return classList[0]  
    if len(dataSet[0])==1:#只有类别列，没有属性列  
        return mahorityCnt(classList)  
    bestFeat = chooseBestFeatureToSplit(dataSet)#获得最优属性下标  
    bestFeatLabel = labels[bestFeat]#获得最优属性  
    myTree = {bestFeatLabel:{}}  
    del(labels[bestFeat])#删除最优属性  
    featValues = [example[bestFeat] for example in dataSet]  
    uniqueVals = set(featValues)  
    for value in uniqueVals:  
        subLabels = labels[:]  
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)#递归计算分类树  
    return myTree  

因为我们递归构建决策树是根据属性的消耗进行计算的，所以可能会存在最后属性用完了，但是分类还是没有算完，这时候就会采用多数表决的方式计算节点分类

def mahorityCnt(classList):#计算最大所属类别  
    classCount = {}  
    for vote in classList:  
        if vote not in classCount.keys():  
            classCount[vote]=0  
        classCount[vote]+=1  
    sortedClassCount = sorted(classCount.items(),key=operator.getitem(1),reverse=True)  
    return sortedClassCount[0][0]  

六、源代码

#coding=utf-8
from math import log
import operator

def createDataSet():
    dataSet = [[1,1,0,'fight'],[1,0,1,'fight'],[1,0,1,'fight'],
               [1,0,1,'fight'],[0,0,1,'run'],[0,1,0,'fight'],
               [0,1,1,'run']]
    lables = ['weapon','bullet','blood']
    return dataSet,lables
def calcShannonEnt(dataSet):#输入训练数据集  
    numEntries = len(dataSet)#计算训练数据集中样例的数量  
    labelCounts = {}  
    for featVec in dataSet:  
        currentLabel = featVec[-1]#获取数据集的标签  
        if currentLabel not in labelCounts.keys():  
            labelCounts[currentLabel]=0  
        labelCounts[currentLabel]+=1 #当前标签实例数+1  
        shannonEnt = 0.0  
        for key in labelCounts:  
            prob = float(labelCounts[key])/numEntries  
            shannonEnt -= prob *log(prob,2)#计算信息熵  
    return shannonEnt
def splitDataSet(dataSet,axis,value):#划分属性，获得去掉axis位置的属性value剩下的样本  
    retDataSet = []  
    for featVec in dataSet:  
        if featVec[axis] == value :  
            reduceFeatVec = featVec[:axis]  
            reduceFeatVec.extend(featVec[axis+1:])#extend()方法接受一个列表作为参数，并将该参数的每个元素都添加到原有的列表中  
            retDataSet.append(reduceFeatVec)#append()方法向列表的尾部添加一个新的元素，只接受一个参数。  
    return retDataSet  
def chooseBestFeatureToSplit(dataSet):#选择最好的特征  
    numFeatures = len(dataSet[0])-1  
    baseEntropy = calcShannonEnt(dataSet)  
    bestInfoGain = 0.0; bestFeature = -1  
    for i in range(numFeatures):  
        featList = [example[i] for example in dataSet]  
        uniqueVals = set(featList)#将特征值放到一个集合中，消除重复的特征值  
        newEntropy = 0.0  
        for value in uniqueVals:  
            subDataSet = splitDataSet(dataSet,i,value)  
            prob = len(subDataSet)/float(len(dataSet))  
            newEntropy += prob * calcShannonEnt(subDataSet)  
        infoGain = baseEntropy - newEntropy#计算信息增益  
        if(infoGain>bestInfoGain):  
            bestInfoGain = infoGain  
            bestFeature = i  
    return bestFeature  
def mahorityCnt(classList):#计算最大所属类别  
    classCount = {}  
    for vote in classList:  
        if vote not in classCount.keys():  
            classCount[vote]=0  
        classCount[vote]+=1  
    sortedClassCount = sorted(classCount.items(),key=operator.getitem(1),reverse=True)  
    return sortedClassCount[0][0]  
  
def createTree(dataSet,labels):#构建分类树  
    classList = [example[-1] for example in dataSet]#获得类别列  
    if classList.count(classList[0]) == len(classList):#所有样本属于同一类别  
        return classList[0]  
    if len(dataSet[0])==1:#只有类别列，没有属性列  
        return mahorityCnt(classList)  
    bestFeat = chooseBestFeatureToSplit(dataSet)#获得最优属性下标  
    bestFeatLabel = labels[bestFeat]#获得最优属性  
    myTree = {bestFeatLabel:{}}  
    del(labels[bestFeat])#删除最优属性  
    featValues = [example[bestFeat] for example in dataSet]  
    uniqueVals = set(featValues)  
    for value in uniqueVals:  
        subLabels = labels[:]  
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)#递归计算分类树  
    return myTree  
  


data,label = createDataSet()
myTree = createTree(data,label)
print myTree

七、运行结果

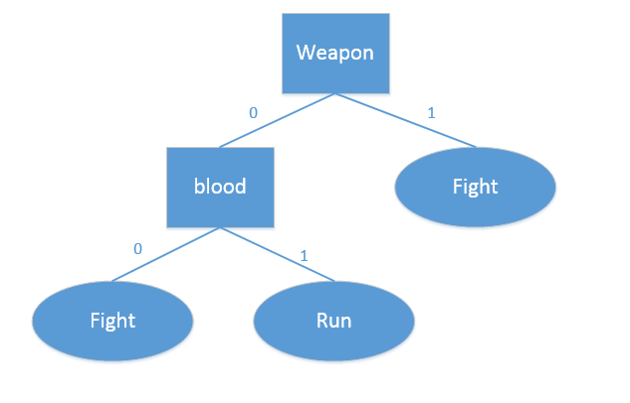
示意图