基本概念(三角分解相关):
在数学中的矩阵论里,置换矩阵是一种系数只由0和1组成的方块矩阵。置换矩阵的每一行和每一列都恰好有一个1,其余的系数都是0。在线性代数中,每个n阶的置换矩阵都代表了一个对n个元素(n维空间的基)的置换。当一个矩阵乘上一个置换矩阵时,所得到的是原来矩阵的横行(置换矩阵在左)或纵列(置换矩阵在右)经过置换后得到的矩阵。
设A是一个方块矩阵。A的LU分解是将它分解成如下形式:
其中L和U分别是下三角矩阵和上三角矩阵。
例如对于一个 的矩阵,就有
的矩阵,就有
-
 。
。
一个LDU分解是一个如下形式的分解:
其中D是对角矩阵,L和U是单位三角矩阵(对角线上全是1的三角矩阵)。
一个LUP分解是一个如下形式的分解:
一个充分消元的LU分解为如下形式:
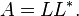
这个分解被称作Cholesky分解。对每一个正定矩阵,Cholesky分解都唯一存在。
矩阵的满秩分解
1. 定义:设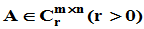 ,若存在矩阵
,若存在矩阵 及
及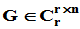 ,使得
,使得
 ,则称其为
,则称其为 的一个满秩分解。
的一个满秩分解。
说明:(1) 为列满秩矩阵,即列数等于秩;
为列满秩矩阵,即列数等于秩; 为行满秩矩阵,即行数等于秩。
为行满秩矩阵,即行数等于秩。
(2)满秩分解不唯一。 (
( 阶可逆方阵),则
阶可逆方阵),则
 ,且
,且
2.当A是满秩(列满秩或行满秩)矩阵时,A可分解为单位矩阵与A本身的乘积,称此时的满秩分解为平凡分解。
R命令:
1)LU分解(包含满秩分解)
library(Matrix)
> m
3 x 3 Matrix of class "dgeMatrix"
[,1] [,2] [,3]
[1,] 2 -1 3
[2,] 1 2 1
[3,] 2 4 2
> l <- lu(m)
> l
'MatrixFactorization' of Formal class 'denseLU' [package "Matrix"] with 3 slots
..@ x : num [1:9] 2 1 0.5 -1 5 0.5 3 -1 0
..@ perm: int [1:3] 1 3 3
..@ Dim : int [1:2] 3 3
> LU <- expand(l) #生成P,L,U
> LU
$L
3 x 3 Matrix of class "dtrMatrix" (unitriangular)
[,1] [,2] [,3]
[1,] 1.0 . .
[2,] 1.0 1.0 .
[3,] 0.5 0.5 1.0
$U
3 x 3 Matrix of class "dtrMatrix"
[,1] [,2] [,3]
[1,] 2 -1 3
[2,] . 5 -1
[3,] . . 0
$P
3 x 3 sparse Matrix of class "pMatrix"
[1,] | . .
[2,] . . |
[3,] . | .
A = P*L*U
P为置换矩阵,L为下单位三角矩阵,U为上三角矩阵;
The decomposition is of the form
A = P L U
where typically all matrices are of size n by n, and the matrix P is a permutation matrix, L is lower triangular and U is upper triangular (both of class dtrMatrix).
Note that the dense decomposition is also implemented for a m by n matrix A, when m != n.
If m < n (“wide case”), U is m by n, and hence not triangular.
If m > n (“long case”), L is m by n, and hence not triangular.
2)Choleskey分解
> A
[1,]
[2,]
[3,]
[4,]
> chol(A)
[1,] 1.414214 0.7071068 0.7071068 0.7071068
[2,] 0.000000 1.2247449 0.4082483 0.4082483
[3,] 0.000000 0.0000000 1.1547005 0.2886751
[4,] 0.000000 0.0000000 0.0000000 1.1180340
> t(chol(A))%*%chol(A)
[1,]
[2,]
[3,]
[4,]
> crossprod(chol(A),chol(A))
[1,]
[2,]
[3,]
[4,]
若矩阵为对称正定矩阵,可以利用Choleskey分解求行列式的值,如:
> prod(diag(chol(A))^2)
[1] 5
> det(A)
[1] 5
若矩阵为对称正定矩阵,可以利用Choleskey分解求矩阵的逆,这时用函数chol2inv(),这种用法更有效。如:
> chol2inv(chol(A))
[1,] 0.8 -0.2 -0.2 -0.2
[2,] -0.2 0.8 -0.2 -0.2
[3,] -0.2 -0.2 0.8 -0.2
[4,] -0.2 -0.2 -0.2 0.8
> solve(A)
[1,] 0.8 -0.2 -0.2 -0.2
[2,] -0.2 0.8 -0.2 -0.2
[3,] -0.2 -0.2 0.8 -0.2
[4,] -0.2 -0.2 -0.2 0.8

























 1287
1287











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








