NOI2022 题解

这里是liuzhangfeiabc的NOI2022题解。
目前更新了两天的t1和t2，两天的t3实在没心情去研究了……
注：非官方题解，不保证绝对正确，做法不一定是官方做法。
注2：代码请见这篇文章。
　
d1t1：传送门https://www.luogu.com.cn/problem/P8496
给定 $n$ 个序列，支持：在某个序列末尾插入元素；删除某个序列末尾的元素；将两个序列首尾相接拼成一个新序列，并销毁原先的两个序列；查询若干个序列（可能重复）首尾相接拼起来形成的新序列的绝对众数（出现次数严格大于一半的数，没有则输出 $-1$）。
鉴于这是简单题，就直接上正解：注意到我们可以使用链表来维护这个尾部插入、尾部删除、拼接的过程，同时用线段树（或哈希表、map等）来维护每个序列中每个数的出现次数，合并两个序列时可以线段树合并（或启发式合并）。
怎么查询绝对众数呢？注意到一种经典的求绝对众数的方法叫“摩尔投票”，即维护数对 $(a,b)$，表示当前元素和计数器。新来一个元素 $x$ 之后，若 $b=0$ 则令 $a=x,b=1$ ，否则若 $a=x$ 则令 $b++$，否则令 $b--$ 。注意到这是一个“两两抵消”的过程，因此如果绝对众数存在，则一定是最后的 $a$ ，再扫一遍来检查它是否为绝对众数即可。
另外注意到，这个过程是具有可加性的，即如果在一个集合上做摩尔投票的结果是 $(a,b)$，在另一个集合上的结果是 $(c,d)$，则可以将它们直接“相加”：若 $a=c$ 则结果为 $(a,b+d)$，否则若 $b>d$ 则为 $(a,b-d)$，否则为 $(c,d-b)$，作为这将两个集合合并后的摩尔投票结果。
于是我们可以直接维护每个集合的众数，然后“钦定”一个摩尔投票结果：设一个集合的元素个数为 $a$ ，众数为 $x$ ，出现次数为 $b$ ，则若 $x$ 是这个集合的绝对众数（即 $2b>a$），就令摩尔投票结果为 $(x,2b-a)$，否则直接设为 $(0,0)$ 即可。
最后，注意由于一个询问中一个集合可能出现多次，出现次数需要用long long存储；另外，如果你你想用deque来维护序列，请千万注意空间限制（由于deque的特性，需要占用大量额外空间，因此如果直接开 $10^6$ 个deque可能会直接MLE）。
总复杂度 $O(n\log n)$ 或 $O(n{\log }^{2}n)$ ，取决于你的具体实现。
　
　
　
d1t2：传送门https://www.luogu.com.cn/problem/P8497
长度为 $n$ 的序列 $a$，每个位置在 $l_i\sim r_i$ 之间。最开始，你有 $k$ 次机会可以使得某个位置 $+1$。接下来，你每次可以选择一个位置，使得 $a_i$ 减小至少 $2$，或者选择一个长度至少为 $3$ 的区间使得其中每个 $a_i$ 都减小 $1$。如果能将所有 $a_i$ 变为 $0$，你就获胜了。问：有多少种初始序列使得你存在获胜方案。
解：先考虑 $k=0,l_i=r_i$ 怎么做：注意，这实际上相当于“给定序列问是否能取胜”。
考虑dp，令 $f[i][j][j’]$ 表示当前处理到第 $i$ 个位置，有 $j$ 个操作二至少要延伸到 $i+2$ 位置，$j’$ 个操作二至少要延伸到 $i+1$ 位置，是否可行。注意：这等价于从 $i$ 及之前开始并延伸过 $i$ 的操作二中，有 $j$ 个是从 $i$ 开始，有 $j’$ 个是从 $i-1$ 及之前开始。
问题是：$j$ 和 $j’$ 应该开多大？朴素地开到值域大小显然是不行的，接下来我们将采用一系列操作将其降到常数大小：
首先，由于我们只需要求出一种方案即可，不关心所有方案的总数，可以给方案添加如下的限制规则：
① 优先使用操作一；
② 操作二的长度尽可能短。
如此可得两条较为显然的结论：
1、不会有两个操作二的区间相同。否则，把这两个操作用操作一代替即可；
2、操作二的长度不会超过 $5$。否则，拆成两个更短的操作二即可。


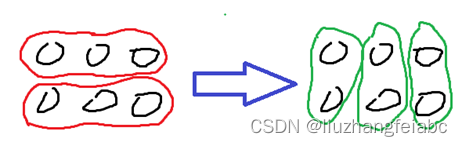
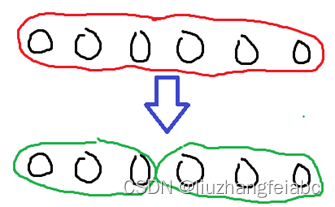
进一步，我们有如下结论：
3、从任意位置开始的操作二的数量至多为 $2$。这是因为，如果有 $3$ 个操作二从同一位置开始，由结论1和2，它们的长度必然分别为 $3,4$ 和 $5$。则可以采用如下方式缩短长度：

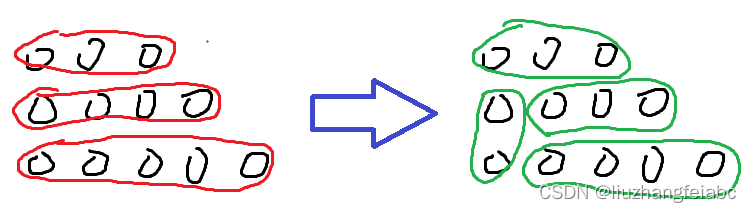
由此我们可以推出如下两条结论：
4、上述dp状态中，$j$ 的值最大只需设为 $2$；
5、上述dp状态中，$j’$ 的值最大只需设为 $6$。
结论5是因为，受到结论2的限制，$j’$ 所涉及到的操作二的起点只可能是 $i-1,i-2$ 或 $i-3$。
如此我们已经可以解决 $k=0,l_i=r_i$ ，只需转移时枚举以 $i$ 开始的操作二有多少个即可。
实际上，进一步分析可以得到的结果是：
6、上述dp状态中，$j’$ 的值最大只需设为 $2$。
证明：对于 $j’=3$ 的情况，只需在结论1和2的限制下列出所有可能的操作二的方案组合，并说明它们均能使用规则①和②进行调整即可。
限于篇幅不再将所有方案一一展开，以下是一个例子：

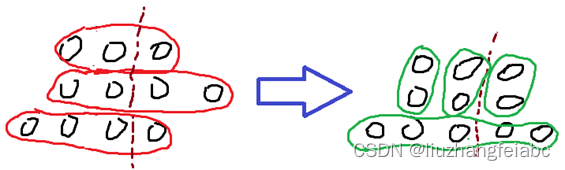
接下来考虑 $l_i=r_i,k\le 100$ 的情况：我们当然可以在先前dp的基础上多记一位：$f[i][p][j][j’]$ 表示当前处理到第 $i$ 个位置，已经用了 $p$ 次 $+1$ 的机会，有 $j$ 个操作二至少要延伸到 $i+2$ 位置，$j’$ 个操作二至少要延伸到 $i+1$ 位置，是否可行。
但是为了后续的分析，我们可以想办法把加的这一维去掉。我们试图求出，为了使得取胜策略存在，在最开始至少要添加多少枚石子。这里我们需要观察到如下结论：除了极特殊的情形外，在一个已经存在取胜策略的局面下添加一枚石子，均存在添加石子的方案使得取胜策略仍存在。
证明：
1、若原先存在一种取胜策略使用了操作一，如将 $i$ 位置移除了 $x$ 枚石子，则只需将新增的石子放入 $i$ 位置，并将该操作改为移除 $x+1$ 石子即可；
2、若原先存在一种取胜策略使用了操作二且区间长度不为 $3$，如操作区间为 $[l,r]$，则只需在将新增的石子放入 $l$ 位置，并将该操作改为一个在 $l$ 位置移除 $2$ 枚石子的操作一和一个对 $[l+1,r]$ 区间执行的操作二即可；
3、若原先存在一种取胜策略使用了操作二且区间不为 $[1,n]$，如操作区间为 $[l,r]（r!=n）$，则只需在将新增的石子放入 $r+1$ 位置，并将该操作改为一个对 $[l,r+1]$ 区间执行的操作二即可；
容易看出，同时不符合以上三种情况的只有两种可能：
① $k=1$，且 $a_i$ 均为 $0$；
② $k=1,n=3$ 且 $a_i$均为 $1$。
特判上述两种情况即可。（忘记特判可能挂成25。）
于是我们可以设 $f[i][j][j’]$ 表示当前处理到第 $i$ 个位置，有 $j$ 个操作二至少要延伸到 $i+2$ 位置，$j’$ 个操作二至少要延伸到 $i+1$ 位置，至少需要额外添加多少枚石子。如果不可达或需要的数量大于 $k$ 则记 $f[i][j][j’]=k+1$ 。此时上述关于 $j$ 和 $j’$ 上界的分析仍然适用。转移时枚举以 $i$ 开始的操作二有多少个即可。
现在考虑 $a_i$ 不再固定的情况，还是先从 $k=0$ 分析：考虑dp套dp，对于一个 $i$ ，把所有可能的 $f[i][j][j’]$ 的值的组合压进状态：$g[i][s]$ 表示考虑到前 $i$ 个位置，$f[i]$ 状态是 $s$ 的方案数。转移时需要枚举下一个 $a_i$ 的值，直接枚举是不可接受的，但只需注意到 $a_i$ 最多枚举到 $8$ 就可以覆盖所有可能的转移了。此时状态总数只有 $2^9=512$ 种，可以预处理所有转移。
对于 $k<=100$ 的情况呢？我们只需对新的 $f$ 进行状压，$s$ 中的每一位从 $0/1$ 变成 $0\sim 101$ 的数。乍一看状态总数高达 $102^9$，但我们只需用dfs/bfs预处理所有有用的状态，即可发现有用的状态数只有 $8765$ 种。
复杂度 $O(nm)$ ，其中 $m$ 为状态数。实际上，其实 $f$ 中 $j=j’=2$ 的状态也是不需要的，可以使得状态数减少到 $7660$ 种，$a_i$ 只枚举到 $7$ 即可。当然或许还有其他状压方法，对状态总数的分析也不一定需要这么繁琐，实测最终的状态数不超过 $30000$ 均能通过此题。
　
　
　
d2t1：传送门https://www.luogu.com.cn/problem/P8499
给定两棵有根树 $T1$ 和 $T2$ ，问能否将 $T1$ 删去若干个非根节点的点后与 $T2$ 同构。保证两棵树的点数之差 $k\le 5$ 。两棵有根树同构定义为一者可以经过重标号后得到另一者，且根在重标号后相同。
解：对于 $k=0$ 的情形，显然我们可以直接做树哈希。鉴于网上的相当多的树哈希写法都是有问题的，这里给出一个正确性较好的树哈希写法：动态地给每种子树分配一个编号（具体实现时可以开一个从哈希值到编号的map），然后对于每个点，将其所有子树的编号（而非哈希值）取出，排序后进行序列哈希。为减少碰撞，底数取得比 $2n$ 大且使用双模数即可。
然后考虑 $k>0$ 的结果：我们记chk(x,y,k)表示 $T1$ 中以 $x$ 为根的子树能否在删除不超过 $k$ 个点的前提下与 $T2$ 中以 $y$ 为根的子树同构。注意这个 $k$ 是必要的，不一定等于二者的子树大小之差，这有助于我们以后剪枝。对于原问题，只需求chk(T1.root,T2.root,|T1|-|T2|)即可。
我们考虑怎样求chk(x,y,k)：首先是一些平凡的情形：如果 $y$ 为空，则只需判断 $x$ 的子树大小是否不超过 $k$；如果 $x$ 的子树与 $y$ 的子树同构，显然结果为true。如果 $x$ 子树大小比 $y$ 小，或 $x$ 子树大小比 $y$ 大超过 $k$，或 $x$ 的儿子数量比 $y$ 少，显然为false。
然后递归地比较 $x$ 与 $y$ 的所有孩子：注意到这一过程实际上是 $x$ 与 $y$ 的孩子两两匹配的过程。假设有两个孩子是同构的，显然可以贪心地匹配；否则，每一个 $x$ 的未匹配上的孩子都需要删除至少一个点才能跟 $y$ 的某个孩子（也可能为空）匹配上，因此没匹配上的 $x$ 孩子数量不能超过 $k$，下设这一数量为 $s$；接下来，在 $y$ 的没匹配上的孩子中补一些空孩子使其数量等于 $s$，然后暴力枚举 $x$ 和 $y$ 的每个没匹配上的孩子，分别设为 $u$ 和 $v$，递归到chk(u,v,k-s+1)（注意这里的 $k-s+1$ 便是考虑到了每个没匹配上的孩子都至少要删一个点这个性质）。最后做一个二分图匹配即可（由于 $k$ 很小，也可以用暴力dfs或霍尔定理代替）。
这看起来是一个最坏 $O(n^2)$ 的大暴力，实际上我们可以看到， chk函数中这个限制 $k$ 起到了很好的剪枝作用，可以证明：每个 $T1$ 中的节点至多参与 $2^k$ 次chk过程（证明过程略）。再算上每个点处的二分图匹配过程，可得总的复杂度上界为 $O(n{2}^k{k}^3)$，当然由于这个上界实际上远远跑不满，因此程序跑得飞快。
　
　
　
d2t2：传送门https://www.luogu.com.cn/problem/P8500
长度为 $n$ 的非负整数序列，给定 $m$ 个限制，形如区间 $[l_i,r_i]$ 内的最小值恰好为 $v_i$ 。求一个合法的序列使得严格逆序对数（即数对 $(i,j)$ 满足 $i<j$ 且 $a_i>a_j$ 的数量）尽可能少。无解输出 $-1$。
解：首先注意到权值范围太大是没有必要的，因为求得是严格逆序对，因此将整个序列全部填为限制中给出的数总是不劣的，因此可以将值域离散化；同时给出多于 $n$ 个取值不同的限制一定是无解的，因此值域可以限制在 $1\sim n$。
先来看“判定是否存在解”的问题，而这其实是一个经典问题：将所有限制升序排序，维护每个位置可能的最小值是多少。每加入一个限制，就相当于对区间 $[l_i,r_i]$ 进行一次整体赋值为 $v_i$ 的操作。最后扫一遍所有的限制，维护区间最小值，查询 $[l_i,r_i]$ 的最小值是否恰好是 $v_i$，如果不是说明这个限制的最小值是取不到的，因此就无解了。
然后，记如此求出的每个位置可能的最小值为 $b_i$ ，接下来该如何操作呢？你可能会设计一系列的贪心策略然后取最优。实际上，这个题的良心之处在于，你随便想一个看起来还算合理的贪心几乎就都是对的！接下来我们不会去严格地证明某一种贪心的正确性，而是从部分分出发，讲解如何想到一个比较合理的贪心策略：
先看部分分B，相当于“给定序列中的一些位置之后求答案”。稍加思索不难发现剩余位置一定是单调不降的，而且正是由于这一特性，你可以对每个位置独立考虑，即仅考虑已经填好的位置对这个位置的贡献，并贪心地令这个贡献最小。如何维护呢？注意到对于位置 $i$ 而言，如果 $j<i$ 且 $a_j$ 已经填好，那么 $i$ 位置填 $[1,a_j-1]$ 会产生一个贡献，反之若 $j>i$ 则是 $[a_j+1,n]$ 会有贡献。我们可以从左往右扫描每个未填的位置，用线段树区间加、区间求最小值来维护每个位置填的贡献最小的数是多少。当外层扫过一个已经填好的数之后，就意味着其贡献区间从 $[1,a_j-1]$ 变成了 $[a_j+1,n]$，在线段树上区间修改即可。
再来看部分分A，即值域只有 $1$ 和 $2$ 的情形。我们可以先将那些最小值为 $2$ 的限制区间全都填上 $2$（然后就不用管这些限制了），然后把剩余位置填上 $1$。接着我们从后到前扫过每一个 $1$，尝试将其变成 $2$。如果变成 $2$ 会使答案变得更优（可以直接记录前后的 $1$ 和 $2$ 各有多少个来判断），并且不会使得某个最小值为 $1$ 的限制区间爆掉，我们就贪心地将其变为 $2$。如何判断会不会使限制区间爆掉呢？我们可以对于每个限制区间，记录一个 $q_i$ 表示这个区间最靠左的能填 $1$ 的位置（这可以在前一步判断是否有解时顺便用线段树时处理出来）。扫描时，维护一个标记 $pos$ 表示从这里到当前位置至少需要有一个 $1$ 以满足限制，扫到区间的右端点时加入区间，更新 $pos$ 的值（与 $q_i$ 取 $\max$），然后如果 $pos=i$ 则说明这里必须填 $1$ 以满足限制，否则就可以随意填了。最后，如果这里还是填了 $1$，则当前的所有限制都已经被满足，置 $pos=0$ 即可。
最后将两个部分分拼成正解。对于已经求得的 $b_i$ 序列，我们从后往前扫描，尝试在不违反限制的前提下将每个位置增大到最佳位置。注意到每一种权值的限制都是彼此独立的，因此可以用与部分分A相同的方式处理每个位置是否需要保持不动以满足限制。然后再用部分分B的思想，贪心地将当前位置修改为能使得当前序列的逆序对数最少的值即可，仍然可以用线段树来维护。具体实现时，你可以先直接在 $b$ 序列的基础上构造出答案序列，再用树状数组求逆序对数。
虽然没有给出严格证明，但结合两档部分分，这一做法还是比较容易想到且易于理解的。复杂度 $O(n\log n)$ 。
　
后记：6000多字的题解终于写完了，感谢你看到最后。
以及不要问我关于“出题人是谁”之类的问题，问就是保密。