NNDL 作业12：第七章课后题

最新推荐文章于 2023-11-13 17:42:40 发布

笼子里的薛定谔

最新推荐文章于 2023-11-13 17:42:40 发布

阅读量560

点赞数 1

分类专栏： DL实验文章标签：深度学习人工智能

本文链接：https://blog.csdn.net/liuzi_hang/article/details/128259204

版权

DL实验专栏收录该内容

28 篇文章 3 订阅

订阅专栏

习题7-1 在小批量梯度下降中，试分析为什么学习率要和批量大小成正比

读过的一篇论文：One weird trick for parallelizing convolutional neural networks 中，有这样一句话：

Since one step in large mini-batch N should match the effectiveness of k accumulative steps in small mini-batch N

意思是在梯度相等的假设下, batch size为N, lr为0.1, 当增大batch size为3 x N, 这一个大batch需要走完之前3个小batch的step, lr为3 x 0.1。

言归正传，调大batch size为什么就要增大学习率呢？

这是因为在比较大batch和小batch时,一般默认都是相同epoch去比较,这样大batch训练iteration次数会更少, 此时如果学习率不做任何调整, 大batch训练更少iteration, 导致拟合程度较低, 精度也会低, 因此需要对学习率做调整。 一个大batch包含样本更多, 避免了小batch包含极端样本的情况, 样本随机梯度方差更小, 优化平面更加平稳，意味着使用大batch计算下来的梯度方向更可信, 因此可以使用一个更大的learning rate (有样本随机梯度、随机梯度方差的数学知识理解起来更加容易)。

一般有两种增大形式：
a. lr = base_lr * sqrt(k)
b. lr = base_lr * k

多说一点，Bag of tricks for Image Classification with Convolutional Neural Networks 这篇文献中，也详细解释如何解决Batch增大带来的问题:

1.linear scaling learning rate: 增大batch size虽然不能改变随机梯度的期望,但是可以降低它的方差 -> 降低了噪声的梯度 -> 因此可以使用一个更大的学习率, 随着batch size增大, 线性提高learning rate, ex: lr=0.1, batch_size=256 -> batch_size=b, lr=0.1xb/256

2.learning rate warmup: 训练初始阶段, 使用一个大的lr会导致数值不稳定(针对分类任务, 网络权值都是随机值, 检测任务一般使用finetune, 数值相对稳定), 在一开始训练时,使用一个小的lr, 当训练稳定后, 逐步恢复到initial lr(恢复方式也比较多, 有线性增大等方式)

习题7-2 在Adam算法中，说明指数加权平均的偏差修正的合理性

Adam算法是Momentum算法和AdaDelta算法的结合体，即使用：

Momentum形式： $m_{t} = \beta _{1}\cdot m_{t-1} + (1-\beta _{1})\cdot g_{t}$
结合AdaDelta形式： $V_{t} = \beta _{2}\cdot V_{t-1}+(1-\beta _{2})\cdot g_{t}^{2}$

前者控制一阶动量，后者控制二阶动量。(具体解释可见：一个框架看懂优化算法之异同 SGD/AdaGrad/Adam - 知乎)
即按照指数移动平均值来计算。

实际使用过程中，参数的经验值是：

$\beta _{1}=0.9,\beta _{2}=0.999$

初始化：
$m_{0}=0,V_{0}=0$

这个时候注意到，在初期， $m_{t},V_{t}$ 都会接近于0，这个估计是有问题的。因此，常常根据下式进行修正:
$\tilde{m}_{t}=m_t/(1-\beta _{1}^{t})$

$\tilde{V}_{t}=V_{t}/(1-\beta _{2}^{t})$

可视化如下：

假设β=0.98时，指数加权平均结果如上图绿色曲线所示。但是实际上，真实曲线如紫色曲线所示，修正这种问题的方法是进行偏移校正（bias correction）。即在每次计算完 $V_{t}$ 后，对 $V_{t}$ 进行如下处理： $\frac{V_{t}}{1-\beta ^{t}}$

在刚开始的时候，t 比较小， $(1-\beta ^{t})<1$ ，这样就将 $V_{t}$ 修正得更大一些，效果是把紫色曲线开始部分向上提升一些，与绿色曲线接近重合。随着t增大， $1-\beta ^{t}\approx 1$ ， $V_{t}$ 基本不变，紫色曲线与绿色曲线依然重合。这样就实现了简单的偏移校正，得到我们希望的绿色曲线。

注：机器学习中，偏移校正并不是必须的。因为，在迭代一次次数后（t较大）， $V_{t}$ 受初始值影响微乎其微，紫色曲线与绿色曲线基本重合。所以，一般可以忽略初始迭代过程，等到一定迭代之后再取值，这样就不需要进行偏移校正了。

习题7-9 证明在标准的随机梯度下降中，权重衰减正则化和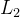 $L_{2}$ 正则化的效果相同.并分析这一结论在动量法和Adam算法中是否依然成立

https://towardsdatascience.com/weight-decay-l2-regularization-90a9e17713cd

这里面详细解释了在标准的随机梯度下降中，权重衰减正则化和 $L_{2}$ 正则化的效果相同，总结如下：

正则化可以定义为我们为了减少泛化误差而不是减少训练误差而对训练算法所做的任何改变。有许多正规化策略。有的对模型添加额外的约束，如对参数值添加约束，有的对目标函数添加额外的项，可以认为是对参数值添加间接或软约束。如果我们仔细使用这些技术，这可以改善测试集的性能。在深度学习的环境中，大多数正则化技术都基于正则化估计器。当正则化一个估计量时，有一个折衷，我们必须选择一个增加偏差和减少方差的模型。一个有效的正则化是使一个有利可图的交易，显著减少方差，而不过度增加偏差.

L2正则化属于正则化技术的一类，称为参数范数惩罚。之所以提到这类技术，是因为在这类技术中，特定参数的范数(主要是权重)被添加到被优化的目标函数中。在L2范数中，在网络的损失函数中加入一个额外的项，通常称为正则化项。那L2正则化和权重衰减是一回事吗？其实L2正则化和权值衰减并不是一回事，但是可以根据学习率对权值衰减因子进行重新参数化，从而使SGD等价。

以λ为衰减因子，给出了权值衰减方程。

在以下证明中可以证明L2正则化等价于SGD情况下的权值衰减：

先看一下L2正则化方程

$C=C_{0}+\frac{\lambda }{2}\left | \left | \omega \right | \right |_{2}^{2}$

再对正则化方程进行求导操作

在得到损失函数的偏导数结果后，将结果代入梯度下降学习规则中，如下式所示。

最终重新排列的L2正则化方程和权值衰减方程之间的唯一区别是α(学习率)乘以λ(正则化项)。为了得到两个方程，用λ来重新参数化L2正则化方程

$\lambda =\frac{\lambda \acute{}}{\alpha }$

将λ'替换为λ，对L2正则化方程进行重新参数化，将其等价于权值衰减方程，如下式所示

$\omega =(1-{\lambda }')\omega -\alpha \Delta C_{0}$ ，其中： $\lambda =\frac{\lambda \acute{}}{\alpha }$

从上面的证明中，可以得证L2正则化在SGD情况下被认为等同于权值衰减，但对于其他基于自适应梯度的优化算法，如Adam, AdaGrad，动量法等，却不是这样。特别是，当与自适应梯度相结合时，L2正则化导致具有较大历史参数和/或梯度振幅的权值比使用权值衰减时正则化得更少。这导致与SGD相比，当使用L2正则化时Adam表现不佳。另一方面，权值衰减在SGD和Adam身上表现的一样好。