算法期末考试复习

最新推荐文章于 2024-08-10 15:25:17 发布
最新推荐文章于 2024-08-10 15:25:17 发布
阅读量690 收藏 15
点赞数 7
分类专栏： 算法 文章标签： 算法 开发语言 c++
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/liyankang/article/details/140794252
版权

算法的定义

算法的三要素

算法由操作、控制结构、数据结构组成

算法的基本性质

  1. 目的性
  2. 分步性
  3. 有序性
  4. 有限性
  5. 操作性

算法的5个重要特性

  1. 有穷性
  2. 确定性
  3. 可行性
  4. 算法有零个或多个的输入
  5. 算法有一个或多个的摘出

算法时间复杂度计算

例题一、
时间复杂度例题1.png``
例题二、
在这里插入图片描述

时间复杂度例题1过程.png

常见时间复杂度数量级

  1. 常数级：O(1)
  2. 对数级：O(log n)
  3. 线性级：O(n)
  4. 多项式级：O(n^c)
  5. 指数级：O(c^n)
  6. 阶乘级：O(n!)

迭代算法

迭代法也称“辗转法”,是种不断用变量的旧值递推出新值的解决问题的方法。
迭代法分为:

  • 递推法(正推法)：（兔子繁殖、最大公约数、振子跳台阶!）是迭代算法的最基本的表现形式，一般来讲，一种简单的递推方式是从小规模的问题推出大规模问题。
  • 倒推法：（猴子吃桃问题、越沙漠）对某些特殊问题采用违反通常习惯的从后往前推解决。

兔子繁殖问题

  • 问题描述
  • 代码实现

辗转相除求最大公约数问题

  • 代码实现
int gcd(int a, int b) {  
 if (b == 0) { 
     return a;  
 }  
 return gcd(b, a % b);  
}

猴子吃桃子问题

  • 问题描述：猴子吃桃问题就是：一个猴子，看到许多的桃子，第一天吃了一半，又吃了一个，第二天也吃了一半，又吃了一个，一直这样下去，到了第10天，只剩下一个桃子了，求猴子吃桃子的过程。
  • 问题分析：
    假设第一天猴子吃了n个，这么说就是**((n/2+1)/2+1)/2+1…/2+1=1**（重复9次因为猴子第一天已经吃了桃子）这样子倒推过来就是**((1+1)*2+1)2…+1)2=n，第一天猴子吃了1个，我们赋值于x,x一直x=(x+1)*2重复9次就可以得出从第10天到第1天猴子吃桃的过程了。
  • 代码实现
int sum=1;//最后剩下1个桃 
for(int i=0;i<=8;i++)//0也算一次，也就是9次 
{
    sum=(sum+1)*2;//重复操作 
    printf("猴子第%d天吃了%d桃\n",9-i,sum);
}

蛮力算法

百钱买百鸡问题

  • 问题描述：公元5世纪末，我国古代数学家张丘建在他所撰写的《算经》中提出了这样一个问题：鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一。百钱买百鸡，问鸡翁、母、雏各几何？
  • 代码实现：
for(int i=0;i<20;i++)	//鸡翁：i只
 for(int j=0;j<33;j++)	//鸡母：jzhi只
     if(i*5 + j*3 + (100-i-j)/3.0 == 100)	//鸡雏：100-i-j只
         //输出结果
         cout<<"方法"<<ans++<<"：\n"<<"鸡翁:"<<i<<endl<<"鸡母:"<<j<<endl<<"鸡雏:"<<100-i-j<<endl;

解数字迷问题

求3个数的最小公倍数

  • 题目描述：输入三个正整数，求它们的最小公倍数（LCM）
  • 代码实现：
// 蛮力搜索最小公倍数
int search(int a, int b, int c) {
    int lcm = -1; // 初始化为-1，表示没有找到解
    for (int i = 1; i <= a * b * c; i++) { // 从1到三数的乘积逐个尝试
        if (i % a == 0 && i % b == 0 && i % c == 0) { // 如果i是三数的公倍数
            lcm = i; // 更新最小公倍数
            break; // 找到一解即可退出循环
        }
    }
    return lcm;
}

狱吏问题

水仙花数问题

  • 题目描述：水仙花数是指一个n位数(n≥3)，它的每个位上的数字的n次幂之和等于它本身（例如：13 + 53+ 3^3 = 153）
  • 代码实现：
// 蛮力搜索3位水仙花数
int search() {
    for (int i = 100; i < 1000; i++) { // 枚举所有3位数
        int sum = 0;
        int remainder = i;
        for (int j = 1; j <= 3; j++) {
            int digit = remainder % 10; // 提取低位上的数字
            remainder /= 10;
                
            sum += pow(digit,3); // 累加幂
        }
            
        // 如果满足水仙花数定义，输出
        if (sum == i) printf("%d\n", i);
            
    }
}

四皇后问题

贴纸问题

分治算法

  • 解题步骤：
    1. 分解:将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题。
    2. 解决:若子问题规模较小而容易被解决则直接解，否则再继续分解为更小的子问题，直到容易解决。
    3. 合并:将已求解的各个子问题的解，逐步合并为原问题的解。
  • 二分法所能解决的问题一般具有以下几个特征:
    1. 该问题的规模缩小到- -定的程度就可以容易解决。
    2. 该问题可以分解为若干个规模较小的相同问题。
    3. 该问题所分解出的各个子问题是相互独立的。
    4. 利用分解出的子问题的解可以合并为该问题的解。

金块问题

  • 问题描述：老板有一袋金块（共n块，n是2的幂（n>=2）），最优秀的雇员得到其中最重的一块，最差的雇员得到其中最轻的一块。假设有一架比较重量的机器，希望用自己最少的比较次数找出最重和最轻的金块，并对自己的程序做复杂性分析。
  • 代码实现：
int a[10]={5,3,7,9,1,6,2,8,4,0}; 
  
void MaxMin(int l , int r , int &fmax , int &fmin){
    int mid = (l+r)/2;	//取中间
  
    //如果区间只有1个元素 
    if(l==r) fmax=fmin=a[mid];
    //区间有2个元素 
    else if(r-l == 1) a[l]<a[r] ? fmax=a[r],fmin=a[l] : fmax=a[l],fmin=a[r];
  
    //区间有多个元素
    else
    {
    int lmax,lmin,	//左边区间的最大最小值 
        rmax,rmin;	//右边区间的最大最小值 
  
    //分左右区间讨论 
    MaxMin(l,mid,lmax,lmin);
    MaxMin(mid+1,r,rmax,rmin);
  
    //两个区间合并讨论
    fmax = max(lmax , rmax);
  
    fmin = min(lmin , rmin);
    }
}

二分查找问题

  • 代码实现：
/* 二分查找问题 */
int binary_search(int arr[], int left, int right, int key) {
    while(left <= right) { // 在区间[left, right]里二分查找关键字key
        int mid = left + (right - left) / 2; // 取中间位置
        if(arr[mid] == key) {
            return mid;
        } else if(arr[mid] < key) { // 如果要查找的值在右半部分
            left = mid + 1; // 查找右半部分
        } else { // 否则在左半部分
            right = mid - 1; // 查找左半部分
        }
    }
    return -1; // 没有找到
}

残缺棋盘问题

  • 问题描述
    1、在棋盘当中存在一个残缺的格子，我们需要用多个三格板将次棋盘覆盖。
    2、给出一个4*4的残缺棋盘摆放方法。（彩色为三格板位置，图中5种不同的颜色对应5块三格板）
    残缺棋盘.png
  • 代码实现：（一个8*8的棋盘，残缺位置为第2行第1列，注意：下面代码数组下标从0开始）
#include <bits/stdc++.h>
#define MAX 100
using namespace  std;
    
int board[MAX][MAX];
int three_plate_num = 1;
void fun(int x,int y,int x0,int y0,int n){
    //当只有一行一列时会退出 
    if(n<=1) return;
    
    int three_plate_id = three_plate_num ++;    //三格板编号
    
    int mid = n/2;    //减小问题的规模
    
    //此时中点位置为 [x+mid][y+mid]
    /*残缺的在左上方时 */
    if(x0 < x+mid && y0 < y+mid){
        fun(x , y , x0 , y0 , mid);                    //对左上方的棋盘递归 
        fun(x , y+mid , x+mid-1 , y+mid , mid);        //对左下方的棋盘递归
        fun(x+mid , y+mid , x+mid , y+mid-1 , mid);    //对右下方的棋盘递归
        fun(x+mid , y , x+mid , y+mid , mid);          //对右上方的棋盘递归
    
        board[x+mid-1][y+mid] = three_plate_id;        //为左下方的棋盘赋值
        board[x+mid][y+mid]   = three_plate_id;        //为右下方的棋盘赋值 
        board[x+mid][y+mid-1] = three_plate_id;        //为右上方的棋盘赋值         
    }
    /*残缺的在左下方时 */
    if(x0 < x+mid && y0 >= y+mid){
        fun(x , y+mid , x0 , y0 , mid);              //对左下方的棋盘递归
        fun(x , y , x+mid-1 , y+mid-1 , mid);       //对左上方的棋盘递归
        fun(x+mid , y+mid , x+mid , y+mid , mid);    //对右下方的棋盘递归
        fun(x+mid , y , x+mid , y+mid-1 , mid);      //对右上方的棋盘递归
    
        board[x+mid-1][y+mid-1] = three_plate_id;    //为左上方的棋盘赋值
        board[x+mid][y+mid]     = three_plate_id;    //为右下方的棋盘赋值 
        board[x+mid][y+mid-1]   = three_plate_id;    //为右上方的棋盘赋值     
    }
    /*残缺的在右上方时 */
    if(x0 >= x+mid && y0 < y+mid){
        fun(x+mid , y , x0 , y0 ,mid);                //对左上方的棋盘递归
        fun(x , y+mid , x+mid-1 , y+mid , mid);       //对左下方的棋盘递归
        fun(x+mid , y+mid , x+mid , y+mid-1 , mid);   //对右下方的棋盘递归
        fun(x , y , x+mid-1 , y+mid-1 , mid);         //对左上方的棋盘递归
    
        board[x+mid-1][y+mid]   = three_plate_id;     //为左下方的棋盘赋值
        board[x+mid][y+mid]     = three_plate_id;     //为右下方的棋盘赋值 
        board[x+mid-1][y+mid-1] = three_plate_id;     //为左上方的棋盘赋值 
    }
    /*残缺的在右下方时 */
    if(x0 >= x+mid && y0 >= y+mid){
        fun(x+mid , y+mid , x0 , y0 , mid);          //对右下方的棋盘递归 
        fun(x , y+mid , x+mid-1 , y+mid ,mid);       //对左下方的棋盘递归
        fun(x , y , x+mid-1 , y+mid-1 ,mid);         //对左上方的棋盘递归
        fun(x+mid , y , x+mid , y+mid ,mid);         //对右上方的棋盘递归
    
        board[x+mid-1][y+mid]   = three_plate_id;    //为左下方的棋盘赋值
        board[x+mid-1][y+mid-1] = three_plate_id;    //为左上方的棋盘赋值 
        board[x+mid][y+mid-1]   = three_plate_id;    //为右上方的棋盘赋值         
    }
}
    
/*打印坐标上的点*/
void print_board(int n){
    for(int i=0 ; i<n ;i++){
        for(int j=0 ; j<n ; j++) cout<<board[i][j]<<"\t";
        cout<<endl;
    }
}
    
int main(){
    //以上面的样例执行一下效果
    fun(0,0,1,0,8);
    print_board(8);
}

求最大子段和问题

  • 问题描述：给定一个数组，求这个数组的连续子数组中，最大的那一段的和。
    如数组[-2,1,-3,4,-1,2,1,-5,4]的最大字段和是[4,-1,2,1]，为6
  • 代码实现：
/* 求最大子段和问题 */
int maxSubArraySum(int arr[], int n) { // 求一个数组中的最大连续子数组之和
    int max_so_far = arr[0]; 
    int curr_max = arr[0];
    for(int i = 1; i < n; i++) {
        curr_max = max(arr[i], curr_max + arr[i]);
        max_so_far = max(max_so_far, curr_max); // 遍历数组并更新最大连续子数组之和
    }
    return max_so_far;
}

求一组数中的第k小的数

  • 问题描述：求出第k小的数
  • 代码实现
/* 求一组数中的第k小的数 */
int select_k(int arr[], int left, int right, int k) { // 选出一个数组中第k小的元素
    if(left == right) { // 如果数组中只有一个元素
        return arr[left]; //直接返回这个元素
    }
        
    int pivotIndex = left + (right - left) / 2; // 选取枢纽元
    pivotIndex = partition(arr, left, right, pivotIndex); // 将数组分为两部分
    if(k == pivotIndex) {
        return arr[k]; //找到第k小的元素
    } else if(k < pivotIndex) {
        return select_k(arr, left, pivotIndex - 1, k); //递归在左面的部分寻找第k小的元素
    } else {
        return select_k(arr, pivotIndex + 1, right, k); //递归在右面的部分寻找第k小的元素
    }
}

贪心算法

  • 概念：
    1. 贪心法(Greedy)又叫登山法，它的根本思想是逐步到达山顶，即逐步获得最优
  • 贪心算法设计思想：
    1. 贪心算法的基本思想是找出整体当中每个小的局部的最优解，并且将所有的这些局部最优解合起来形成整体上的一个最优解。
  • 能够使用贪心算法的问题必须满足下面的两个性质:
    1. 整体的最优解可以通过局部的最优解来求出。
    2. 一个整体能够被分为多个局部，并且这些局部都能够求出最优解。

币种统计问题

  • 问题描述：
  • 代码实现：
/* 币种统计问题 */
int changeCoins(int coins[], int n, int k) { // 计算金额k可能的组合数
    int dp[k + 1]; 
    memset(dp, 0, sizeof(dp)); // 初始化数组
        
    dp[0] = 1; // 只有一种表示 1 元的方法，即 1 个 1 元硬币
    for(int i = 0; i < n; i++) { // 从前往后遍历硬币的面额
        for(int j = coins[i]; j <= k; j++) { // 在所有的金额中找到该面额可表示的组合数
            dp[j] += dp[j - coins[i]];
        }
    }
    return dp[k]; //返回表示金额k的组合数
}

动态规划的基本思想

  • 基本思想：
    1. 将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到的子问题往往不是互相独立的。
  • 求解步骤：
    1. 分析最优子结构性质。
    2. 递归地定义最优值。
    3. 以自底向上的方式计算出最优值。
    4. 根据计算最优值时得到的信息，构造最优解。

上台阶问题

  • 问题描述：
  • 解题思路：这是一个求斐波那契数列题。
  • 代码实现：
int fibonacci(int n){
    int dp[n+1];
        
    //边界 
    dp[0]=dp[1]=1;
        
    for(int i=2;i<=n;i++)
        dp[i] = dp[i-1]+dp[i-2];
            
    return dp[n];
}

路径数问题

  • 问题描述：一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。问总共有多少条不同的路径？
    路径数问题.png代码实现：
int DP(int m , int n){
    int dp[m][n];	//m行n列 
        
    //边界，第一行和第一列只有一种方法可以到达
    for(int i=0;i<m;i++) dp[i][0]=1;
    for(int i=0;i<n;i++) dp[0][i]=1;
        
    for(int i=1;i<m;i++)
        for(int j=1;j<n;j++)
            f[i][j] = f[i-1][j] + f[i][j-1];
                 
    return dp[m-1][n-1]; 
}

路径数值最小问题

  • 问题描述：给定一个有权重的有向图，求从起点到终点的所有路径中，路径权重之和最小的长度。
    路径最小值.png
  • 由图可判断最小路径和为：1+3+1+1+1 =7
  • 代码实现：
int a[N][N];	//用来存放二维数组当中的权重
int DP(int n){
    int dp[n][n];
        
    //边界
    dp[0][0] = a[0][0];	//起点无选择 
        //到第一列的元素只能由上一元素向下移动得到
    for(int i=1;i<n;i++) dp[i][0] = dp[i-1][0] + a[i][0];	
        //到第一行的元素只能由上一元素向右移动得到
    for(int i=1;i<n;i++) dp[0][i] = dp[0][i-1] + a[0][i];	
                 
    for(int i=1;i<n;i++) 
        for(int j=1;j<n;j++)
            dp[i][j] = min(dp[i-1][j] , dp[i][j-1]) + a[i][j];
        
    return dp[n-1][n-1];
}

最大子段和问题

  • 问题描述：给定一个数组，求这个数组的连续子数组中，最大的那一段的和。
    如数组[-2,1,-3,4,-1,2,1,-5,4]的最大字段和是[4,-1,2,1]，为6。
  • 解题思路：状态转移方程：result=max(a[i] , result+a[i])
  • 代码实现：
int a[N+1];	//存放数组
int DP(int n){
    int result;
    int sum=0;
        
    for(int i=1;i<=n;i++){
        //	    不取前面的，取前面的
        result = max(a[i] , result+a[i]);
        sum = max(sum , result);	//更新最大和 
    }
                 
    return sum; 
}

0-1背包问题

  • 问题描述：有n个物品，它们有各自的体积和价值，现有给定容量的背包，如何让背包里装入的物品具有最大的价值总和？
  • 代码实现：（特别说明：如果使用二维数组，j的枚举顺序无关紧要。若使用的是一维数组，那么j必须要逆序枚举）
//二维数组
int DP(int n,int m){	//物品数量，背包最大容量
    int dp[n+1][m+1];
    memset(dp,0,sizeof(dp));
    
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)	//j用来表示背包当前的容量
    // 如果当前背包容量不足以装下当前物品，那么最大价值等于上一个状态的最大价值
            if(j<w[i])	dp[i][j]=dp[i-1][j];
    // 可以装下当前物品，比较不装入该物品的价值和装入该物品后的价值，取最大值
            else dp[i][j] = max(dp[i-1][j] , dp[i-1][j-w[i]]+v[i]);
    
    //由于i、j都是递增遍历，只需输出最后一个即可
    return dp[n][m];
}
    
 //一维数组
int DP(int n,int m){
    int dp[m+1];
        
    memset(dp,0,sizeof(dp));
        
    for(int i=1;i<=n;i++)
        for(int j=m;j>=w[i];j--)
            dp[j] = max(dp[j] , dp[j-w[i]]+v[i]);
                
    int result = dp[0];
    for(int i=1;i<=m;i++) 
        result = max(result , dp[i]);
    return result;
}

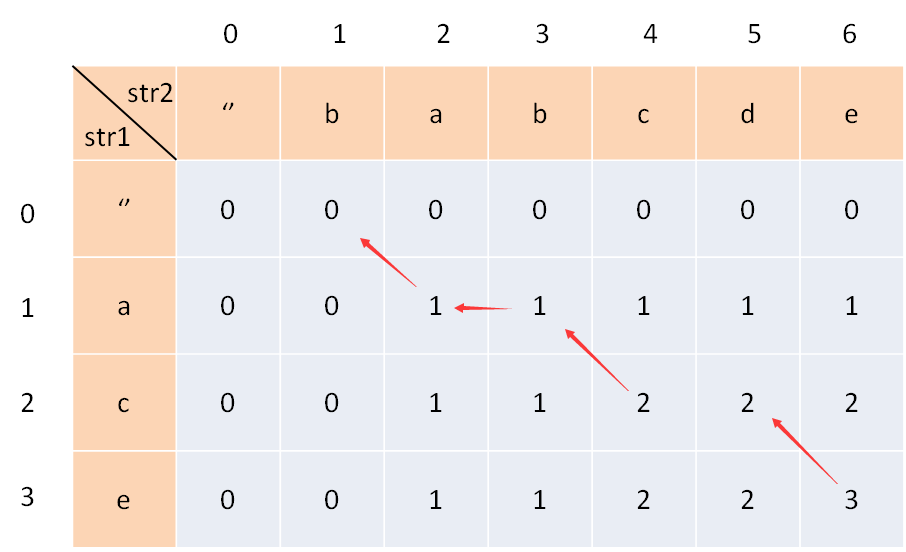
最长公共子序列（LCS）

  • 问题描述：输入: str1 = "abcde", str2 = "ace" 最长公共子序列是 "ace"：它的长度是 3
  • 图片演示：LCS.png
  • 代码实现：
int LCS(char s1[] ,char s2[] , int len1 , int len2){
    int dp[len1+1][len2+1];
    memset(dp,0,sizeof(dp));

    for(int i=1;i<=len1;i++)
        for(int j=1;j<=len2;j++)
            if(s1[i] == s2[j]) dp[i][j] = dp[i-1][j-1] + 1;
            else dp[i][j] = max(dp[i-1][j] , dp[i][j-1]);

    return dp[len1][len2];
}

数塔问题：

  • 问题描述：有一个n行的数塔，数塔上有若干数字。问从数塔的最高点到底部，在所有的路径中，经过的数字的和最大为多少？如图：
    数塔问题.png
  • 其中7—3—8—7—5的路径经过数字和最大，为30。解题思路：
    1. 面对数塔问题，使用贪心算法显然是行不通的，比如给的样例，如果使用贪心算法，那选择的路径应当是7—8—1—7—5，其经过数字和只有28，并不是最大。
    2. 而用深搜DFS很容易算出时间复杂度为 O(2n) （因为每个数字都有向左下和右下两种选择），行数一多必定超时。
    3. 动态规划可以选择从上到下，也可以从下到上。值得注意的是，从上到下要注意数组下标问题。
  • 代码实现：
//动态方法：	
int a[N];	//存放数塔
int DP(int n){
    for(int i=n-1;i>0;i--)	//从下往上 
        for(int j=1;j<=i;j++)
            if(a[i+1][j] >= a[i+1][j+1]) //判断左下和右下的谁更大 
                a[i][j] += a[i+1][j];
            else 
                a[i][j] += a[i+1][j+1];
    return a[1][1];	//此时的顶层是底层累加上去的，故为最大 
}

回溯算法设计思想

  • 概念：
    1. 有“通用的解题法”之称，可以系统地搜索一个问题的所有解和任意解。
    2. 有递归和非递归之分

批处理作业调度问题

  • 问题描述：给定 n 个作业的集合 j =( j1 ,j2,···, jn )。每一个作业 j [i]都有两项任务分别在两台机器上完成。每一个作业必须先由机器1处理，然后由机器2处理。作业 j [i]需要机器 j 的处理时间为 t [j] [i]，其中 i =(1,2,···, n ), j =(1,2)。对于一个确定的作业调度，设 F [j] [i]是作业 i 在机器 j 上的完成处理的时间。所 有作业在机器2上完成处理的时间之和 f = sigma F [2] [i]称为该作业调度的完成成时间之。
  • 代码实现：
#include <bits/stdc++.h>
using namespace std;
  
int x[100];    //作业调度顺序 
int bestx[100]; //当前最优作业调度
int m[100][3];
//各作业所需的处理时间
//m[j][i]代表第j个作业在第i台机器上的处理时间
int f1=0;//机器1完成处理时间
int f2=0;//机器2完成处理时间
int cf=0;//完成时间和
int bestf=10000;//当前最优值，即最优的处理时间和
int n;//作业数量 
  
void Backtrack(int t)
{    //t用来指示到达的层数（第几步，从0开始），同时也指示当前执行完第几个任务/作业
    int tempf,j;
  
    if(t>n) //到达叶子结点，搜索到最底部
    {
        if(cf<bestf)	//是更优解 
        {
            //更新最优调度序列
            for(int i=1; i<=n; i++)
                bestx[i]=x[i];
            //更新最优目标值
            bestf=cf;
        }
    }
  
    else    //非叶子结点
    {
        for(j=t; j<=n; j++) //j用来指示选择了哪个任务/作业（也就是执行顺序）
        {
  
            f1+=m[x[j]][1];//选择第x[j]个任务在机器１上执行，作为当前的任务
            tempf=f2;//保存上一个作业在机器2的完成时间
            f2=(f1>f2?f1:f2)+m[x[j]][2];//保存当前作业在机器2的完成时间
            cf+=f2;               //在机器2上的完成时间和
            //如果该作业处理完之后，总时间已经超过最优时间，就直接回溯。
            //剪枝函数
            if(cf<bestf) //总时间小于最优时间
            {
                swap(x[t],x[j]);  //交换两个作业的位置，把选择出的原来在x[j]位置上的任务调到当前执行的位置x[t]
                Backtrack(t+1);   //深度搜索解空间树，进入下一层
                swap(x[t],x[j]); //进行回溯，还原，执行该层的下一个任务 //如果是叶子节点返回上一层
            }
            //回溯需要还原各个值
            f1-=m[x[j]][1];
            cf-=f2;
            f2=tempf;
        }
    }
}
int main(){
    int i,j;
    cout<<"请输入作业数："<<endl;
    cin>>n;
  
    cout<<"请输入在各机器上的处理时间"<<endl;
    for(i=1; i<=2; i++) //ｉ从１开始
      for(j=1; j<=n; j++)
          cin>>m[j][i];//第j个作业,第i台机器的时间值
    for(i=1; i<=n; i++)
      x[i]=i;//初始化当前作业调度的一种排列顺序
    Backtrack(1);
  
    cout<<"调度作业顺序："<<endl;
    for(i=1; i<=n; i++)
      cout<<bestx[i]<<' ';
    cout<<endl;
  
    cout<<"处理时间："<<endl;
    cout<<bestf;
    return 0;
}

n皇后问题

  • 问题描述：一个如下的 6 × 6 的跳棋棋盘，有六个棋子被放置在棋盘上，使得>每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。
    N皇后问题描述.png
  • 代码实现：
#include <bits/stdc++.h>
using namespace std;
#define N 15	//最大皇后数量
int q[N];	//存放皇后的列下标 
int n;	//皇后的个数
int ans = 0;	//答案个数
    
//判断i行j列是否可以放皇后 
int isOK(int i,int j){
    for(int k=1;k<i;k++)	//遍历q数组 
        if(j==q[k]  ||  abs(i-k)==abs(j-q[k])) 	return 0;
        //列相等   或者	横纵坐标的距离相等（即在对角线上）
    return 1;		
}
    
//放置皇后到棋盘上(从第i行开始)
void place(int i)
{
    //放置了n个皇后 
    if(i>n) {	//打印结果，输出q数组即可 
        if(ans++ <3){	//按题目要求，打印3次
            for(int i=1;i<=n;i++)
                cout<<q[i]<<" ";
            cout<<endl;
        }
    } else {
        //试探列的位置 
        for(int j=1;j<=n;j++){
            if( isOK(i,j) ){
                q[i]=j;
                place(i+1);//继续放置下一行的皇后 
            } 
        }
    }
}
    
int main (){
    cin>>n;
    place(1);	//注意：题目的下标从1开始
    cout<<ans;
}
悟解了
关注
  • 7
    点赞
  • 踩
  • 15
    收藏
    觉得还不错? 一键收藏
  • 打赏
    打赏
  • 0
    评论
专栏目录
研究生算法期末考试复习资料总计docx
06-02
在计算机科学中，算法设计与分析是至关重要的领域，尤其对于研究生...以上这些知识点都是算法设计与分析的核心，对于研究生的期末考试至关重要。理解并掌握这些算法不仅有助于考试，也能在解决实际问题时提供强大工具。
数据结构与算法期末考试复习试题.pdf
03-25
数据结构与算法期末考试复习试题
数据结构及算法期末考试复习试题.docx
10-05
数据结构及算法期末考试复习试题 数据结构是计算机科学中的一门重要课程， 涉及到数据的存储、组织和操作。数据结构有多种不同的类型，如数组、链表、栈、队列、树、图等。算法是解决问题的步骤，包括查找、排序、...
数据结构与算法期末考试复习试题.docx
10-25
在这份期末考试复习试题中，我们看到几个关键的知识点，它们涵盖了数据结构的基本概念、算法的时间复杂度分析以及特定数据结构的操作特性。 1. 数据结构的分类：根据描述，我们知道数据结构主要分为线性结构和非...
算法分析与设计期末考试复习考点
05-16
算法分析与设计期末考试复习考点 本资源摘要信息涵盖了算法分析与设计的重要知识点，涵盖算法的基本概念、算法分析、递归算法、动态规划、贪心算法、回溯法、分支限界法等多个领域。 一、算法的基本概念 * 算法...
day 9 回溯算法
m0_73924943的博客
08-08 263
优化后的比之前的在叶子结点少递归一层。在排序candidates后，碰到target<0的情况直接结束本层的遍历，后面没遍历到的也不用遍历了。1.目标数n一直在随i的加入减小，如果目标数n已经<0，那么剪枝。即path中的数已经大于目标数了。利用数组去重，因为题目的数值范围小，所以可以尽量使用。剪枝优化：（对每层循环遍历的范围进行了缩小）2.对for循环i的遍历范围进行缩小。也可以不用st数组去重。
day021二叉树最后章节
m0_62956971的博客
08-06 580
思路: 二叉搜索树的中序遍历就是有序升序数组，所以想要将它在转换成二叉树，我想到的方法就是通过递归来做，通过中间节点找到二叉搜索树的根节点，然后根据left和right双指针逐层递归构造左右子树。思路:最开始没有判断当当前节点小于最小值时，当前节点的右侧节点的情况，和当前节点大于最大值时，当前节点的左节点的情况，所以出错了，因此要在代码中判断一下这两种情况。思路: 累加树 由题意可知，在二叉搜索树中的递归顺序是右中左的顺序，创建一个新的函数，进行右中左的遍历，在遍历中要将节点的值记录下来，用来做累加。
代码随想录算法训练营day36：动态规划04：1049.最后一块石头的重量II；494.目标和；474.一和零
weixin_65180740的博客
08-07 889
力扣题目链接(opens new window)有一堆石头，每块石头的重量都是正整数。每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：如果 x == y，那么两块石头都会被完全粉碎；如果 x!= y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。最后，最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下，就返回 0。输入：[2,7,4,1,8,1]输出：1。
基于LQR算法的机器人轨迹跟踪控制详解
慕羽★的博客
08-10 1383
本文详细介绍了基于线性二次型调节器（LQR）算法的机器人轨迹跟踪控制方法。首先，文章通过建立基于运动学模型的离散状态方程，来描述机器人的当前状态与目标状态之间的关系，并利用此模型进行状态误差的计算。接着，通过设定状态量和控制量的权重矩阵（Q和R），使用LQR算法求解控制输入u，旨在最小化状态偏差和控制成本，以实现精确的轨迹跟踪。此外，文章还分析了LQR算法在ros_motion_planning运动规划库中的实现，通过源代码详解了误差量化、状态方程动态矩阵的建立、反馈控制增益的计算以及最终控制向量的生成等关
用霍夫变换算法来识别图像中圆形的轮廓cv::HoughCircles
追赶时代的博客
08-06 425
霍夫变换 圆形轮廓检测 cv::HoughCircles
浙大版《C语言程序设计（第3版）》题目集
qq_67330059的博客
08-09 285
其中a和b是用户传入的参数，函数返回的是两者中较大的数。
(回溯) LeetCode 39. 组合总和
最新发布
zth12212003的博客
08-10 752
本题也十分建议练习，巩固回溯的基础同时可以应对相关的变题时间复杂度：O(S)，S 为所有可行解的长度之和；空间复杂度：O(target)。
代码随想录算法训练营day37｜动态规划part05
qq_39065682的博客
08-08 212
感觉今天学的技巧性都挺强的，完全背包的还得再看看；
算法日记day 33（动归之斐波那契数|爬楼梯）
m0_74980681的博客
08-08 333
要求每次可以爬1阶或者2阶，逆向思维可以理解为，当我们上到最后一阶楼梯时，可以迈一阶楼梯dp[n-1]，或者迈两阶楼梯上dp[n-2]，因此可得最终爬上去n阶台阶的方法共有dp[n-1]+dp[n-2]种方法，dp的方法是爬到第n阶台阶总共有多少种方法，而不是走了几步，因此递推关系仍是斐波那契数列。已知斐波那契数列递推式为dp[i]=dp[i-1]+dp[i-2]，因此求第n个数只需要逐渐相加获得。1. 1 阶 + 1 阶 + 1 阶。1. 1 阶 + 1 阶。2. 1 阶 + 2 阶。
算法测试.
cxj0695的博客
08-06 382
现在，尼克需要在公司中建立一个 "主管-同级 "关系的树状层次结构(也就是说，除了一名员工外，每名员工都有一名主管)。有N种豆子，这些豆子只能靠颜色来区分，每个豆子都有它的美味度；题目要求的是每种颜色豆子里面的美味度最小值的最大值；题目意思就是给你t个字符串，让你找出每个串与codeforces这个串有多少不同的字母；贪心，把m条关系按照代价排序，当x的大于y的，且y没有主管即可能让x当y的主管；运用map来存储最小的美味度，然后循环遍历找最大的美味度就好；的主管，但需支付额外费用。
LeetCode——3131.找出与数组相加的整数I
玄昌盛不会编程
08-08 212
LeetCode——3131.找出与数组相加的整数I
CSP-J 复赛 模拟题7 and 解析
xingdjk888的博客
08-08 793
素数，又称质数，是指除 11 和其自身之外，没有其他约数的正整数。例如 2,3,5,132,3,5,13 都是素数，而 4,9,12,184,9,12,18 则不是。特别地，规定 11 不是素数（因此自然数的质因数分解就是唯一的）。如果一个数字的任意前缀所对应的数字都是一个素数，那么我们称这个数字是一个超级素数，例如：233233是一个超级素数，因为它的三个不同的前缀2,23,2332,23,233都是素数。而457457本身虽然是一个素数，但是它的前缀4,454,45却不是素数，所以457457不是一个超
【LeetCode 1991 找到数组的中间位置 / LeetCode 724 寻找数组的中心下标】中间索引问题
牧码人的博客
08-06 468
这段代码的时间复杂度为 O(n^2)，其中 n 是数组 nums 的长度。这是因为在最坏的情况下，需要对每个索引 i 都重新计算左侧和右侧元素的和，每个计算的时间复杂度为 O(n)。该方法的空间复杂度为常数：复杂度为O(1)，因为它使用的额外空间不随输入数组的大小变化。所有的变量都占用固定的空间，无论数组有多长，这些变量占用的空间大小都是相同的。
代码随想录算法训练营第五十六天｜108.冗余连接 、109.冗余连接II
m0_73129864的博客
08-09 342
本题的本质是 ：有一个有向图，是由一颗有向树 + 一条有向边组成的 （所以此时这个图就不能称之为有向树），现在让我们找到那条边 把这条边删了，让这个图恢复为有向树。首先寻找两个节点的根节点，如果根节点相同则直接返回，否则将一个节点的根设置为另一个节点的根。方法实现寻根操作，并应用了路径压缩技术，递归地将直接或间接的父节点指向根节点，优化了查找效率。方法判断两个节点是否在同一个集合中，通过比较它们的根节点是否相同。方法重新初始化并查集，使每个节点的父节点指向自己。，初始化并查集，然后循环读取每对节点。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

悟解了

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值