离散序列的一致性度量方法：动态时间规整（DTW）

动态时间规整：Dynamic Time Warping（DTW），是一种衡量两个离散时间序列相似度的方法，主要特点是在序列长度不一或x轴无法完全对齐的情况下，用满足一定条件的的时间规整函数描述两者之间的时间对应关系。DTW算法在各种模式匹配任务中被广泛使用，如语音识别、动态手势识别和信息检索等中。

一、算法简述

在数字信号处理领域中，时间序列是数据的一种常见表示形式。对于时间序列处理来说，对于许多的信号处理任务，如图像匹配、视频跟踪和姿态识别等，通常需要度量两个离散序列的相似性。而这一步骤说难不难，说易也不易，这往往需要考虑信号采样、噪声干扰等实际问题。

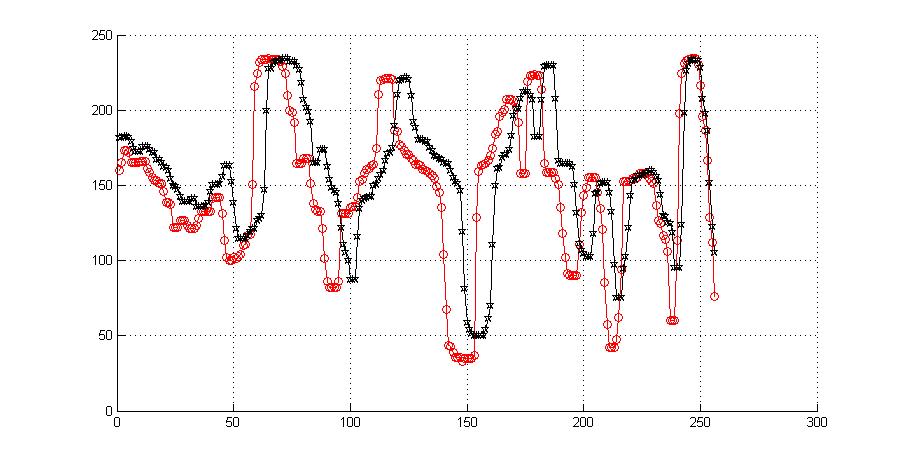
在很多情况下，单纯的相似性度量方法无法很好度量两个序列的一致性，如在语音识别中经常出现两段时间序列的长度不相等的情况（或下图中的情况），此时从直观上都能观察到，直接使用欧几里得距离、相关系数等方法进行度量并不靠谱，此时点对点运算变得无意义。

DTW的主要思路如下：

1.假定两个待匹配的离散数据分别为A={A(1),A(2),…,A(m)}和B={B(1),B(2),…,B(m)}，其中下标为1的元素为序列的起点，下标为m/n的元素为序列终点。

2.为了对齐A,B两个序列，这里采用了“动态规划”的方法，首先构造一个m*n的矩阵，用于存放两序列点对点之间的距离（一般可使用欧氏距离），距离越小表明两点之间的相似度越高。

3.该部分是DTW算法的核心，这里把矩阵看成一个网格，算法的目的可总结为寻找一条通过此矩阵网格的最优路径，该路径通过的网格点即为两个离散序列经过对齐后的点对。

4.找到最优路径后，DTW算法定义了一个归整路径距离(Warp Path Distance)，通过使用所有相似点之间距离的和，来衡量两个时间序列之间的相似性。

二、归整路径距离计算方法：