HDU 1710 Binary Tree Traversals

最新推荐文章于 2021-05-07 08:03:37 发布

lizhaowei213

最新推荐文章于 2021-05-07 08:03:37 发布

阅读量349

点赞数

分类专栏：树

本文链接：https://blog.csdn.net/lizhaowei213/article/details/50991035

版权

树专栏收录该内容

2 篇文章 0 订阅

订阅专栏

Binary Tree Traversals

Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 5102 Accepted Submission(s): 2335

Problem Description

A binary tree is a finite set of vertices that is either empty or consists of a root r and two disjoint binary trees called the left and right subtrees. There are three most important ways in which the vertices of a binary tree can be systematically traversed or ordered. They are preorder, inorder and postorder. Let T be a binary tree with root r and subtrees T1,T2.

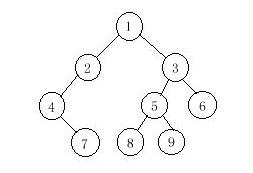
In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.

In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.

In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.

Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.

Input

The input contains several test cases. The first line of each test case contains a single integer n (1<=n<=1000), the number of vertices of the binary tree. Followed by two lines, respectively indicating the preorder sequence and inorder sequence. You can assume they are always correspond to a exclusive binary tree.

Output

For each test case print a single line specifying the corresponding postorder sequence.

Sample Input

  
  
   
   9
1 2 4 7 3 5 8 9 6
4 7 2 1 8 5 9 3 6

Sample Output

  
  
   
   7 4 2 8 9 5 6 3 1

Source

HDU 2007-Spring Programming Contest

和二叉树相关的问题基本都是递归问题。
这道题题意很简单。给出二叉树的前序和中序遍历，求后续遍历。
做法:递归建树+后续遍历。
前序遍历和中序遍历的关系如下.
前序遍历的第一个节点，一定是根节点，所以在中序遍历中找到这个节点，那么其左边的所有节点在左子树，右边的所有节点在右子树。
那么将这两棵子树看成新的二叉树，递归这个过程。就完成建树的过程。

#include <stdio.h>
const int MAXN=1005;
int preArray[MAXN],inArray[MAXN];
typedef struct TreeNode
{
        int key;
        TreeNode* left;
        TreeNode* right;
}TreeNode;
TreeNode* root;
TreeNode* buildTree(int* pre,int preSize,int* in)
{
        TreeNode* temp;
        for(int i=0;i<preSize;i++)
        {
                if(pre[0]==in[i])
                {
                        TreeNode* node=new TreeNode;
                        node->key=in[i];
                        node->left=buildTree(pre+1,i,in);
                        node->right=buildTree(pre+i+1,preSize-i-1,in+i+1);
                        return node;
                }
        }
        return NULL;
}

void postOrder(TreeNode* thisNode)
{
        if(thisNode==NULL)
                return ;
        postOrder(thisNode->left);
        postOrder(thisNode->right);
        if(thisNode==root)
                printf("%d\n",thisNode->key);
        else
                printf("%d ",thisNode->key);
}

int main()
{
        int n;
        while(scanf("%d",&n)>0)
        {
                for(int i=0;i<n;i++)
                        scanf("%d",&preArray[i]);
                for(int i=0;i<n;i++)
                        scanf("%d",&inArray[i]);
                root=buildTree(preArray,n,inArray);
                TreeNode* t=root;
                postOrder(t);
        }
        return 0;
}