Python-tsne可视化

目录

1、简介

tsne(minist)

colormap

2、使用

代码（plt.scatter()画散点图）

绘图颜色选择

代码（sns.scatterplot() 画散点图）

3、补充

度分布（直接用）

可视化整个图（直接用）

tsne可视化节点表示空间（需要训练，下面3个可视化使用定义在了同1个函数中）

熵直方图（需要训练）

注意力权重可视化 （需要训练）

4、补充图（交互）可视化工具

---

---

1、简介

最近需要用到可视化，核心就是tsne+颜色选择使用。

t-SNE是目前来说效果最好的数据降维与可视化方法，但是它的缺点也很明显，比如：

• 占内存大，运行时间长。
• 专用于可视化，即嵌入空间只能是2维或3维。
• 需要尝试不同的初始化点，以防止局部次优解的影响。

但是，当我们想要对高维数据进行分类，又不清楚这个数据集有没有很好的可分性（即同类之间间隔小，异类之间间隔大），可以通过t-SNE投影到2维或者3维的空间中观察一下。如果在低维空间中具有可分性，则数据是可分的；如果在高维空间中不具有可分性，可能是数据不可分，也可能仅仅是因为不能投影到低维空间。 参考文献：

tsne(minist)

参考

• 源自

• 数据降维与可视化——t-SNE（补充了3D绘图）

• t-SNE算法的基本思想及其Python实现（上面的补充）

from sklearn.manifold import TSNE
from sklearn.datasets import load_iris,load_digits
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np
%config InlineBackend.figure_format = "svg"

digits = load_digits()
X_tsne = TSNE(n_components=2, random_state=33).fit_transform(digits.data)
X_pca = PCA(n_components=2).fit_transform(digits.data)

font = {"color": "darkred",
        "size": 13, 
        "family" : "serif"}

plt.style.use("dark_background")
plt.figure(figsize=(8.5, 4))
plt.subplot(1, 2, 1) 
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=digits.target, alpha=0.6, 
            cmap=plt.cm.get_cmap('rainbow', 10))
plt.title("t-SNE", fontdict=font)
cbar = plt.colorbar(ticks=range(10)) 
cbar.set_label(label='digit value', fontdict=font)
plt.clim(-0.5, 9.5)
plt.subplot(1, 2, 2)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=digits.target, alpha=0.6, 
            cmap=plt.cm.get_cmap('rainbow', 10))
plt.title("PCA", fontdict=font)
cbar = plt.colorbar(ticks=range(10)) 
cbar.set_label(label='digit value', fontdict=font)
plt.clim(-0.5, 9.5)
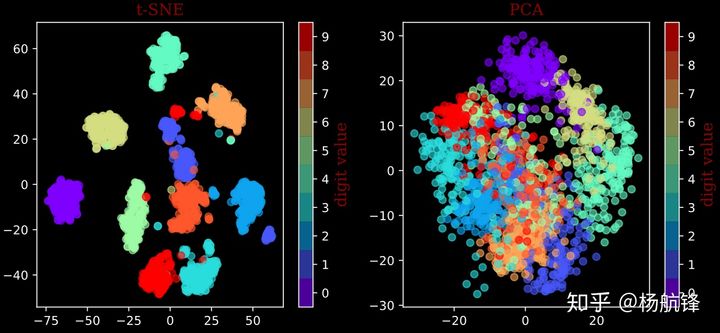
plt.tight_layout()

从实验结果可以看出  tsne算法降维后的可视化效果要远远好于 pca 算法。

colormap

源自

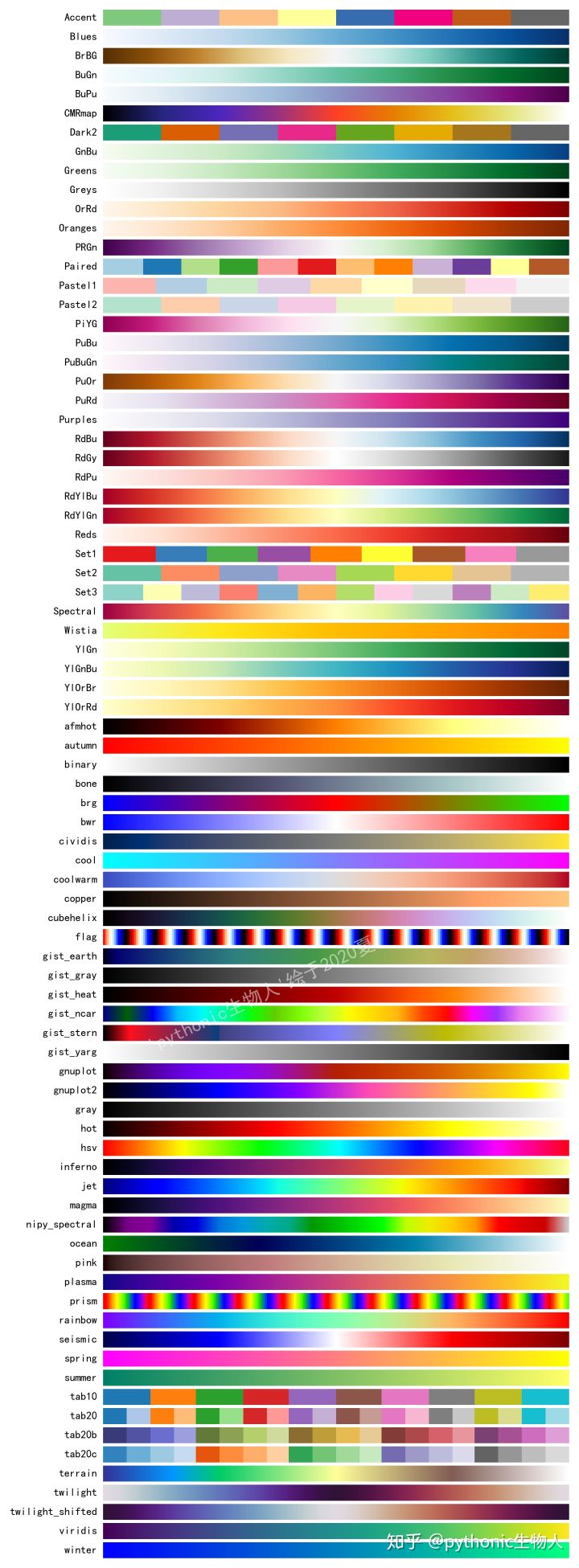
colormap颜色通过matplotlib的cm模块调用，print(dir(cm))即可输出所有的名称，共计81种（不包含反向色条，例如'Reds'的反向色条'Reds_r'），详细如下：

['Accent', 'Blues', 'BrBG', 'BuGn', 'BuPu', 'CMRmap', 'Dark2', 'GnBu', 'Greens', 'Greys', 'OrRd', 'Oranges', 'PRGn', 'Paired', 'Pastel1', 'Pastel2', 'PiYG', 'PuBu', 'PuBuGn', 'PuOr', 'PuRd', 'Purples', 'RdBu', 'RdGy', 'RdPu', 'RdYlBu', 'RdYlGn', 'Reds', 'Set1', 'Set2', 'Set3', 'Spectral', 'Wistia', 'YlGn', 'YlGnBu', 'YlOrBr', 'YlOrRd', 'afmhot', 'autumn', 'binary', 'bone', 'brg', 'bwr', 'cividis', 'cool', 'coolwarm', 'copper', 'cubehelix', 'flag', 'gist_earth', 'gist_gray', 'gist_heat', 'gist_ncar', 'gist_stern', 'gist_yarg', 'gnuplot', 'gnuplot2', 'gray', 'hot', 'hsv', 'inferno', 'jet', 'magma', 'nipy_spectral', 'ocean', 'pink', 'plasma', 'prism', 'rainbow', 'seismic', 'spring', 'summer', 'tab10', 'tab20', 'tab20b', 'tab20c', 'terrain', 'twilight', 'twilight_shifted', 'viridis', 'winter']

每个 colormap到底包含哪些颜色了，绘制了一张图（高清的，欢迎放大食用），便于查询：

2、使用

代码（plt.scatter()画散点图）

# tsne可视化
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE 
"""
可视化
n_components=2 控制降维后的维度
输入：需要降维的矩阵 X shape=(m,n) m:代表样本数量，n:代表样本长度

返回：降维后的矩阵X_norm shape=(m,2)
"""
def visualize(out, color):
   
    out = out.detach().cpu().numpy()#模型输出label概率值
    color = color.detach().cpu().numpy() #data的标签不是类别
    # color = color.cuda().data.cpu().numpy()#效果同上
    # z = TSNE(n_components=2).fit_transform(out.detach().cpu().numpy()) #必须先将2个gpu上的tensor输入变成numpy矩阵形式
    z = TSNE(n_components=2).fit_transform(out)
 
    plt.figure(figsize=(10, 10))
    plt.xticks([])
    plt.yticks([])
 
    # plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="Set2") #颜色浅
    plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="rainbow") #颜色鲜艳
    # plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap=plt.cm.get_cmap('rainbow')) #同上
    plt.title("t-SNE")
    plt.tight_layout()
    plt.savefig('plot_hanacmnode.jpg')
    plt.show()
    

调用

    """
    可视化
    """
    model.eval()
    out = model(gs, features)
    # visualize(out, color=num_classes)
    visualize(out, color=labels)

绘图颜色选择

默认颜色

set2

randow

代码（sns.scatterplot() 画散点图）

参考