1.知识回顾
在前面一篇文章中,我们讨论了ID3算法和C4.5算法生成和剪枝决策树的过程,本篇文章我们主要讨论CART算法,其英文全称是Classification And Regression Trees,也就是分类与回归树,从名字上也可以看出,CART算法既可以用来分类,也可以用来回归。相比于前两种算法,CART算法的应用更加广泛,它是很多高级集成学习框架的基础,比如GBDT和XGBoost(在后面的文章中也会学习到)。
我们首先来说一下CART算法与前两种算法的不同之处。首先,CART算法既可以执行分类任务也可以执行回归任务,而ID3算法和C4.5算法只能执行分类任务;其次,CART算法生成的决策树为二叉树,其它两种算法生成的决策树为多叉树;最后就是上一篇文章所提到的特征选择的准则不同,ID3算法采用最大信息增益,C4.5算法采用最大信息增益比,CART算法则采用最小基尼指数来选择特征。
下面我们还是从特征选择、决策树生成和决策树剪枝三个步骤来讨论CART算法。
2.特征选择
在讨论特征选择之前,先补充一点上一篇文章中所漏掉的东西。在上一篇文章中,我们使用的贷款申请的例子来自于李航老师的《统计学习方法》,但是书中只讨论了特征的取值为离散值(离散型特征)的情况,比如年龄的取值只有青年、中年和老年,但我们在实际使用过程中会经常遇到特征的取值为连续值(连续型特征)的情况,比如年龄就取值为真实的年龄,17,18,20,30这种。下面我们来讨论一下三种算法对于离散型特征和连续型特征都是怎么选择的。
ID3算法是只适用于特征取值为离散值的情况的,C4.5算法和CART算法都是通过连续值离散化的思想来处理特征取值为连续值的情况的。也就是说,当数据集中有特征取值为连续值时,就不再考虑用ID3算法了,可以选择C4.5算法或CART算法。
当特征为连续型特征时:
要确定最优特征首先应该找到最优切分点。C4.5算法和CART算法都是先对连续值进行离散化,然后根据某个指标来确定最优切分点进而确定最优特征。对于C4.5算法,这个指标就是信息增益比;对于CART算法,这个指标则是基尼指数。基尼指数的计算公式如下:
Gini
(
D
)
=
1
−
∑
k
=
1
K
(
∣
C
k
∣
∣
D
∣
)
2
Gini
(
D
∣
A
)
=
∣
D
1
∣
∣
D
∣
Gini
(
D
1
)
+
∣
D
2
∣
∣
D
∣
Gini
(
D
2
)
\text{Gini}(D)=1-\sum_{k=1}^{K}(\frac{|C_k|}{|D|})^2 \\ \text{Gini}(D|A)=\frac{|D_1|}{|D|}\text{Gini}(D_1)+\frac{|D_2|}{|D|}\text{Gini}(D_2)
Gini(D)=1−k=1∑K(∣D∣∣Ck∣)2Gini(D∣A)=∣D∣∣D1∣Gini(D1)+∣D∣∣D2∣Gini(D2)其中,
∣
D
∣
|D|
∣D∣表示数据集
D
D
D的样本数量,
∣
D
1
∣
|D_1|
∣D1∣和
∣
D
2
∣
|D_2|
∣D2∣则表示子集的样本数量。
接下来我们来看一下C4.5算法和CART算法对连续型特征的离散化处理与特征选择过程。过程如下图所示:
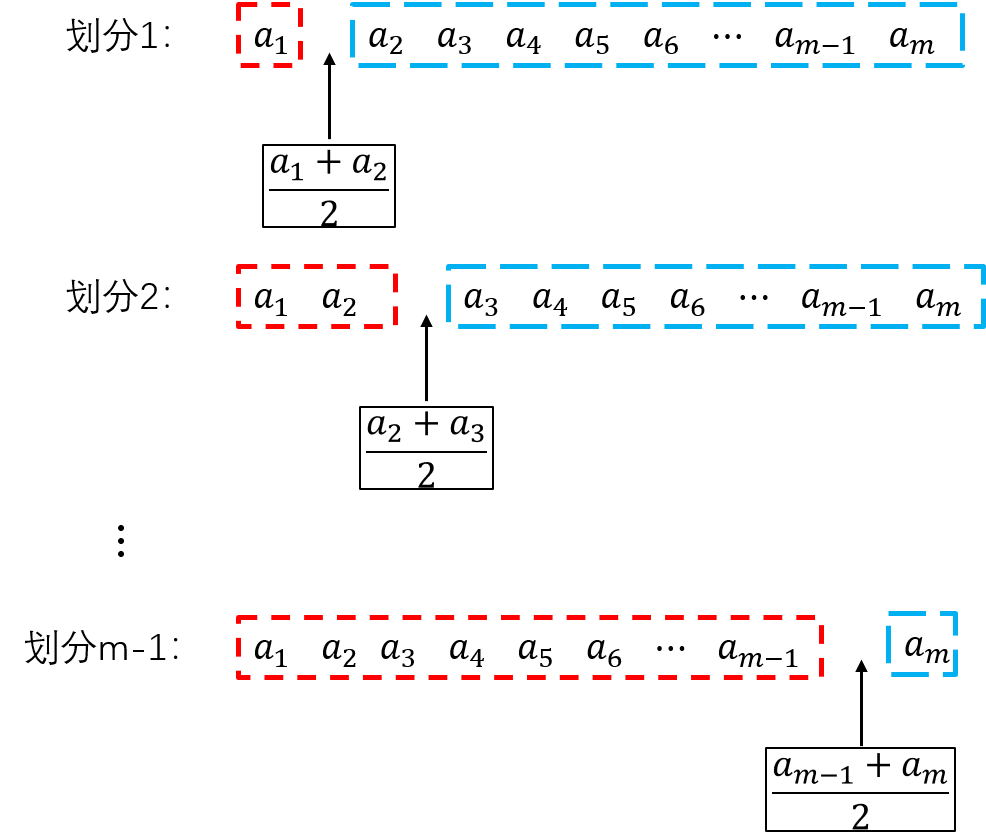
其中, a 1 , a 2 , . . . , a m a_1,a_2,...,a_m a1,a2,...,am为在数据集 D D D中某个连续型特征 A A A的 m m m个取值,并将它们从小到大排列,即 a 1 < a 2 < . . . < a m a_1 < a_2 < ... < a_m a1<a2<...<am。C4.5算法和CART算法都是通过相邻两个连续值的均值来作为切分点,将 m m m个连续值离散化为小于这个切分点和大于这个切分点的两个离散值。连续值离散化后就是要进行特征和切分点的选择了。可以发现 m m m个离散值有 m − 1 m-1 m−1个切分点,也就是说有 m − 1 m-1 m−1种划分方式,每种划分方式将数据集 D D D划分为 D 1 D_1 D1和 D 2 D_2 D2两个子集。对于CART算法,接下来就是要算出每种划分的基尼指数,基尼指数最小的划分对应的切分点就是最优切分点;C4.5算法则是算出每种划分的信息增益比。这时就选择出了在此连续型特征下的最优切分点。
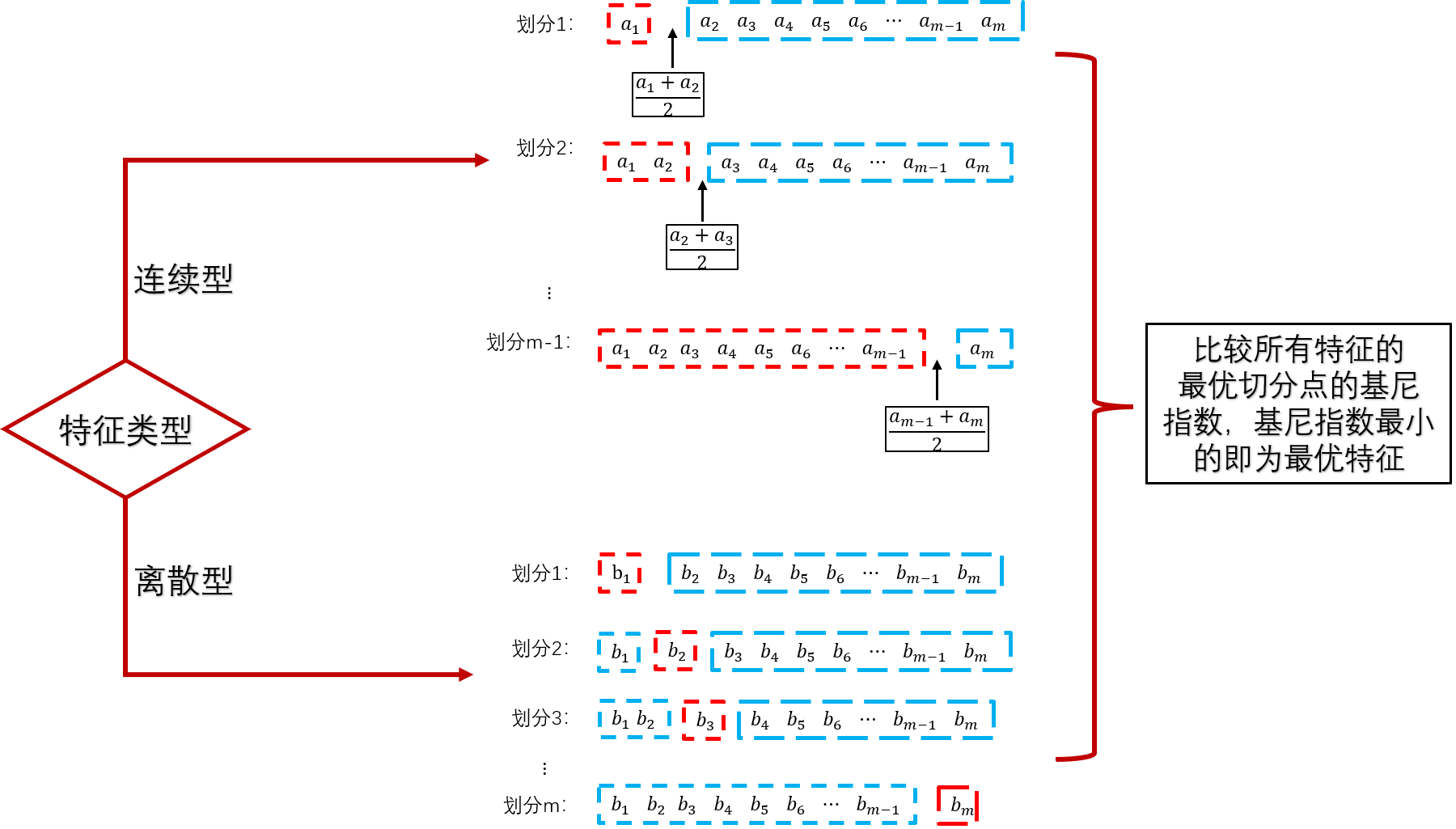
当特征为离散型特征时:
对于离散型特征,CART算法与ID3算法、C4.5算法有很大区别。如果离散特征值多于两个,那么ID3算法和C4.5算法会在结点上根据特征值划分出多叉树。但是CART算法则不同,无论离散特征值有几个,在结点上都划分成二叉树。如下图所示,假设离散型特征
B
B
B有
m
m
m个取值,分别为
b
1
,
b
2
,
.
.
.
,
b
m
b_1,b_2,...,b_m
b1,b2,...,bm:

CART算法是将符合其中某个特征取值的分为一类,而不符合这个特征取值的分为另一类。比如图中的划分1,CART算法将符合取值
b
1
b_1
b1的样本分为一类,将不符合
b
1
取
值
的
b_1取值的
b1取值的,也就是符合其他特征取值的样本分为另一类。
m
m
m个特征取值就有
m
m
m种划分方式,计算每种划分下的基尼指数,最后选择基尼指数最小的一个划分作为最优的特征划分。
上面我们讨论了CART算法针对某个特征怎么选择最优切分点,有了各个特征的最优切分点后,就可以选择最优特征了。具体地,比较每个特征的最优切分点的基尼指数,基尼指数最小的即为最优特征。过程如下图所示:
3.决策树生成
3.1 分类树
首先介绍一下CART算法生成分类决策树的流程:
- 输入:训练数据集 D D D,停止计算的参数条件。
- 输出:二叉决策树。
根据训练数据集,从根结点开始,递归地对每个结点进行以下操作,构建二叉决策树:
(1) 设结点的训练数据集为
D
D
D,识别各个特征的类型,是离散型还是连续型,对每种类型使用上文相应的处理方法并计算每个划分下的基尼系数,找出每个特征下的最优切分点;然后通过比较每个特征的最优切分点的基尼指数大小,基尼指数最小的即为最优特征。
(2) 根据这个最优特征和最优切分点,将数据集划分成两个子集
D
1
D_1
D1和
D
2
D_2
D2,同时建立当前结点的左右结点,左结点的数据集为
D
1
D_1
D1,右结点的数据集为
D
2
D_2
D2。生成子结点后将此最优特征的最优切分点剔除。
(3) 对左右的子结点递归的调用(1)-(2)步,生成决策树。
算法停止的条件是结点中的样本个数小于预定阈值,或样本集的基尼指数小于预定阈值(样本基本属于同一类),或者没有更多特征。
注意: ID3算法和C4.5算法生成子结点后是将上一步的特征剔除,而CART算法是将上一步特征的取值剔除。也就是说在CART算法中一个特征可以参与多次结点的生成,ID3算法和C4.5算法中每个特征最多只能参与一次结点的生成。
我们还是以贷款申请的例子来理解CART算法生成决策树的过程,数据集如下:
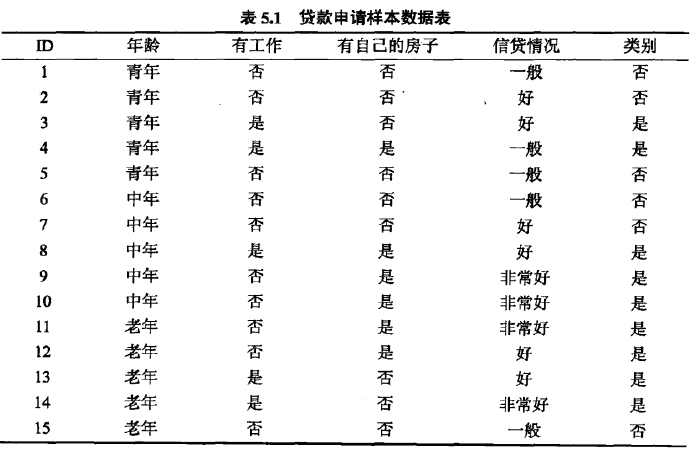
求解过程如下:

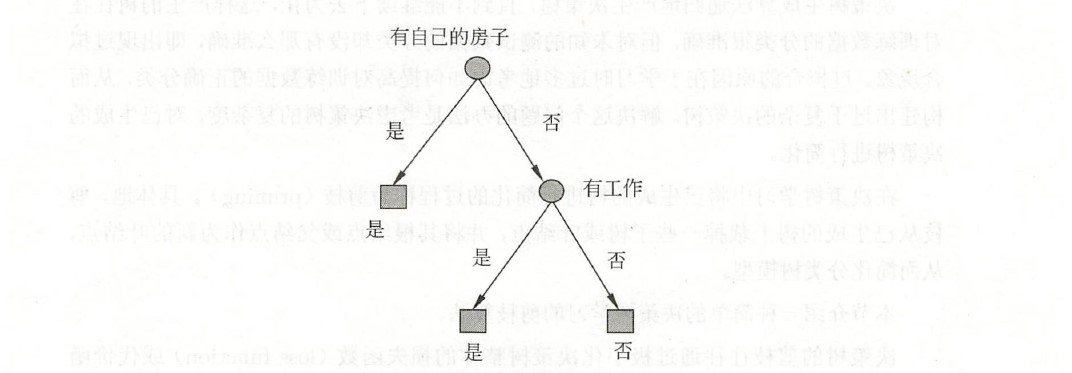
最后生成的决策树如下:
3.2 回归树
我们首先还是来看一下CART算法生成回归树的流程。
- 输入:训练数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } D=\{(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),...,(\boldsymbol{x}_N,y_N)\} D={(x1,y1),(x2,y2),...,(xN,yN)},停止条件。
- 输出:回归树 f ( x ) f(x) f(x)。
(1)选择最优切分变量
j
j
j和最优切分点
s
s
s。具体地,采用启发式的方法,选择第
j
j
j个变量
x
(
j
)
x^{(j)}
x(j)和它的取值
s
s
s来作为切分变量和切分点,并据此定义两个区域:
R
1
(
j
,
s
)
=
{
x
∣
x
(
j
)
≤
s
}
R
2
(
j
,
s
)
=
{
x
∣
x
(
j
)
>
s
}
R_1(j,s)=\{x|x^{(j)} \le s\} \\ R_2(j,s)=\{x|x^{(j)} > s\}
R1(j,s)={x∣x(j)≤s}R2(j,s)={x∣x(j)>s}然后求解:
j
,
s
min
[
c
1
min
∑
x
i
∈
R
1
(
j
,
s
)
(
y
i
−
c
1
)
2
+
c
2
min
∑
x
i
∈
R
2
(
j
,
s
)
(
y
i
−
c
2
)
2
]
_{j,s}^{\text{min}} \bigg[\ _{c_1}^{\text{min}}\sum_{\boldsymbol{x}_i \in R_1(j,s)}(y_i-c_1)^2+\ _{c_2}^{\text{min}}\sum_{\boldsymbol{x}_i \in R_2(j,s)}(y_i-c_2)^2]
j,smin[ c1minxi∈R1(j,s)∑(yi−c1)2+ c2minxi∈R2(j,s)∑(yi−c2)2]对固定的切分变量可以找到在此切分变量下的最优切分点
s
s
s,遍历所有的切分变量就能找到最优的切分变量
j
j
j,构成一个对
(
j
,
s
)
(j,s)
(j,s)。
(2)用选定的最优
(
j
,
s
)
(j,s)
(j,s)对将输入空间划分为两个子区域并决定相应的输出值。
c
^
m
=
1
N
m
∑
x
i
∈
R
m
(
j
,
s
)
y
i
,
m
=
1
,
2
\hat{c}_m=\frac{1}{N_m}\sum_{\boldsymbol{x}_i \in R_m(j,s)}y_i,\ \ m=1,2
c^m=Nm1xi∈Rm(j,s)∑yi, m=1,2
(3)继续对两个子区域调用步骤(1)和(2),直至满足停止条件。
(4)将输入空间划分为
M
M
M个区域
R
1
,
R
2
,
.
.
.
,
R
M
R_1,R_2,...,R_M
R1,R2,...,RM,生成回归决策树:
f
(
x
)
=
∑
m
=
1
M
c
^
m
I
(
x
∈
R
m
)
f(x)=\sum_{m=1}^{M}\hat{c}_mI(x \in R_m)
f(x)=m=1∑Mc^mI(x∈Rm)可以发现,与分类树不同的是,回归树是通过最小化平方误差来进行特征选择的。
对于回归树,最关键的其实就是两个问题:
- 最优切分变量和最优切分点的选取。
- 切分后子区域的输出值的求解。
下面我们以一个例子来讲解最优切分点的选取过程,例子来源于https://www.bilibili.com/video/BV1Bb4y1r7DQ。
| ID | 甜度 | 好吃程度评分 |
|---|---|---|
| 1 | 0.05 | 5.5 |
| 2 | 0.15 | 7.6 |
| 3 | 0.25 | 9.5 |
| 4 | 0.35 | 9.7 |
| 5 | 0.45 | 8.2 |
这个例子是桃子的甜度与好吃程度的关系。共有5个样本,甜度取值为0-0.5,好吃程度评分取值为1-10。在这个例子中只有一个输入变量,即为甜度,我们需要找到在甜度这个变量下的最优切分点。
当切分点
s
=
0.1
s=0.1
s=0.1的时候,可以将输入空间的样本划分为
R
1
=
{
1
}
R_1=\{1\}
R1={1}和
R
2
=
{
2
,
3
,
4
,
5
}
R_2=\{2,3,4,5\}
R2={2,3,4,5}。此时:
c
^
1
=
5.5
c
^
2
=
7.6
+
9.5
+
9.7
+
8.2
4
=
8.75
\hat{c}_1=5.5 \\ \hat{c}_2=\frac{7.6+9.5+9.7+8.2}{4}=8.75
c^1=5.5c^2=47.6+9.5+9.7+8.2=8.75
此划分下的平方误差为:
(
5.5
−
5.5
)
2
+
(
7.6
−
8.75
)
2
+
(
9.5
−
8.75
)
2
+
(
9.7
−
8.75
)
2
+
(
8.2
−
8.75
)
2
=
3.09
(5.5-5.5)^2+(7.6-8.75)^2+(9.5-8.75)^2 \\ +(9.7-8.75)^2+(8.2-8.75)^2=3.09
(5.5−5.5)2+(7.6−8.75)2+(9.5−8.75)2+(9.7−8.75)2+(8.2−8.75)2=3.09同理,我们可以求出在其他切分点时的平方误差。
s
=
0.2
时
,
平
方
误
差
为
3.53
s
=
0.3
时
,
平
方
误
差
为
9.13
s
=
0.4
时
,
平
方
误
差
为
11.52
s=0.2时,平方误差为3.53 \\ s=0.3时,平方误差为9.13 \\ s=0.4时,平方误差为11.52
s=0.2时,平方误差为3.53s=0.3时,平方误差为9.13s=0.4时,平方误差为11.52根据平方误差最小化准则,所以我们选择切分点
s
=
0.1
s=0.1
s=0.1为在甜度这个变量下的最优切分点。不过在实际应用中变量肯定不止一个,这时还需要选择最优变量,其实就是对每个变量分别求其最优切分点,然后再从中选出平方误差最小的即为最优变量。
4.决策树的剪枝
CART剪枝算法就是前一篇文章所讨论的代价复杂度剪枝算法(Cost Complexity Pruning,CCP)。但是,CART算法的CCP过程与ID3算法和C4.5算法有些不同,我们接下来就来讨论一下CART算法剪枝的过程。
我们首先还是给出损失函数:
C
α
(
T
)
=
C
(
T
)
+
α
∣
T
∣
C_{\alpha}(T)=C(T)+\alpha|T|
Cα(T)=C(T)+α∣T∣其中,
T
T
T为任意子树,
C
(
T
)
C(T)
C(T)为对训练数据的预测误差(如基尼指数或均方误差),
∣
T
∣
|T|
∣T∣为子树的叶子结点个数,
α
≥
0
\alpha \ge 0
α≥0为权衡训练数据的拟合程度与模型复杂度的参数。
对于固定的 α \alpha α一定存在使损失函数 C α ( T ) C_{\alpha}(T) Cα(T)最小的子树,也就是说不同的 α \alpha α会对应着不同的最优子树。在前一篇文章中,我们讨论到ID3算法和C4.5算法中参数 α \alpha α是人为给定的,但此时求得的决策树只是在这个 α \alpha α下最优的子树,人为给定的 α \alpha α不一定就是最理想的 α \alpha α,所以在CART算法中, α \alpha α不再是人为给定。
在CART算法中,将 α \alpha α从小增大, 0 = α 0 < α 1 < . . . < α n < + ∞ 0=\alpha_0<\alpha_1<...<\alpha_n<+\infty 0=α0<α1<...<αn<+∞,产生一系列的小区间 [ α i , α i + 1 ) , i = 0 , 1 , . . . , n [\alpha_i,\alpha_{i+1}),i=0,1,...,n [αi,αi+1),i=0,1,...,n,每一个小区间都对应着一个最优子树,这样就得到了一个最优子树序列 { T 0 , T 1 , . . . , T n } \{T_0,T_1,...,T_n\} {T0,T1,...,Tn}。Breiman等人证明了这个序列中的子树是嵌套的, T 0 T_0 T0即为未剪枝的完整决策树, T 1 T_1 T1为 T 0 T_0 T0进行剪枝后的子树, T 2 T_2 T2为 T 1 T_1 T1进行剪枝后的子树。得到了这个最优子树序列后便可以利用K折交叉验证的方法来从中选取最优子树了。K折交叉验证就是将训练数据集分割成K个子集,一个单独的子集被保留作为验证模型的数据,其他K-1个子集用来训练。交叉验证重复K次,每个子集验证一次,平均K次的结果得到评测指标(比如准确率),评测指标最好的子树即为最优决策树。
具体地,从完整树
T
0
T_0
T0开始剪枝,对
T
0
T_0
T0的任意结点
t
t
t,假设以
t
t
t为根结点的子树为
T
t
T_t
Tt,则这个子树未被剪掉之前其损失函数为:
C
α
(
T
t
)
=
C
(
T
t
)
+
α
∣
T
t
∣
C_{\alpha}(T_t)=C(T_t)+\alpha|T_t|
Cα(Tt)=C(Tt)+α∣Tt∣当这个子树被剪掉后,即将这个子树用一个叶结点代替时,损失函数为:
C
α
(
t
)
=
C
(
t
)
+
α
C_{\alpha}(t)=C(t)+\alpha
Cα(t)=C(t)+α当
α
=
0
\alpha=0
α=0或者当
α
\alpha
α充分小时,此时对模型的复杂程度惩罚很小,偏向于生成大的决策树,一定有:
C
α
(
T
t
)
<
C
α
(
t
)
C_{\alpha}(T_t) < C_{\alpha}(t)
Cα(Tt)<Cα(t)当
α
\alpha
α增大到某个值时有:
C
α
(
T
t
)
=
C
α
(
t
)
C_{\alpha}(T_t)=C_{\alpha}(t)
Cα(Tt)=Cα(t)此时若再增大
α
\alpha
α,将会有:
C
α
(
T
t
)
>
C
α
(
t
)
C_{\alpha}(T_t) > C_{\alpha}(t)
Cα(Tt)>Cα(t)使等号成立的这个
α
\alpha
α即为是否要剪枝的临界值,因为此时剪或不剪的损失值相同,而剪了模型更简单,所以此时便需要进行剪枝。
此时,对
T
0
T_0
T0中每一个内部结点
t
t
t,计算:
g
(
t
)
=
C
(
t
)
−
C
(
T
t
)
∣
T
t
∣
−
1
g(t)=\frac{C(t)-C(T_t)}{|T_t|-1}
g(t)=∣Tt∣−1C(t)−C(Tt)将最小的
g
(
t
)
g(t)
g(t)设为
α
1
\alpha_1
α1,并在
T
0
T_0
T0中剪去
g
(
t
)
g(t)
g(t)最小的
T
t
T_t
Tt,此时得到的子树即为在区间
[
α
1
,
α
2
)
[\alpha_1,\alpha_2)
[α1,α2)下的最优子树
T
1
T_1
T1。
再对 T 1 T_1 T1按上述步骤进行剪枝得到 T 2 T_2 T2,如此递归下去便得到最优子树序列 { T 0 , T 1 , . . . , T n } \{T_0,T_1,...,T_n\} {T0,T1,...,Tn},最后再通过交叉验证便得到最优子树 T α T_{\alpha} Tα
给出完整CART剪枝算法的流程如下:

5.参考资料
1.李航《统计学习方法》
2.https://www.sohu.com/a/290362448_654419
3.https://www.zhihu.com/question/22697086
4.https://www.cnblogs.com/xingshansi/p/6847334.html
5.https://www.cnblogs.com/keye/p/10564914.html
推荐阅读:
决策树(1)——ID3算法与C4.5算法的理论基础与python实现
公众号:MyLearningNote























 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










