德国坦克问题及频率学派与贝叶斯学派

转载：Tony's blog: 德国坦克问题及频率学派与贝叶斯学派 (tonysh-thu.blogspot.com)

这是一个看起来很基础很简单的经典问题：假设所有的德国坦克是从1开始按自然数递增编号的，坦克的总数为N，也就是说坦克的最大编号为N。盟军在战斗中共随机俘获/击毁了k辆坦克，且这些坦克的最大编号为m，那么应当如何对N的大小进行估计？

本问题以应用于二战时对德军产能的实际估计而得名，在这个问题的解决上，基于统计的方法取得了非常大的成功，取得了惊人的准确成果。而这个基本问题的解决方法，体现了统计理论中频率学派与贝叶斯学派的不同。

一、原始问题

这个问题在Wikipedia上有详细的介绍和解法：

http://en.wikipedia.org/wiki/German_tank_problem

频率学派和贝叶斯学派对这个问题的理解和解法是不同的，但他们求解时都用到了下面这个显而易见的结论：

已知N和k，则观测到的最大值为m的概率为C(m-1,k-1)/C(N,k)，其中C(x,y)为从x中取y的组合数。即P(m|N,k)=C(m-1,k-1)/C(N,k)。

1. 频率学派

频率学派对原问题的结论是：

N=m(1+1/k)-1

这个结论有一个很直观的解释，就是平均来说观测到的k个序号应该是均匀等间隔的分布在1~N这个范围内的，而去掉观测到的最大的m，剩下的k-1个序号应该均匀等间隔的分布在1~(m-1)这个范围内，根据这个分布的间隔可以估计m距离最大值N的距离。

在上面的wikipedia的link里，推导用了一个很奇葩的方式（虽然它是对的。。），先求给定N，k情况下观测到的最大值的期望，再令这个期望等于m。于是这种方法得到的估计是一个无偏估计（估计值的数学期望与真实值相等），再说明这个估计是最小方差的无偏估计（MVUM）。

wiki页面里的置信区间计算（Confidence intervals部分）我也觉得不太能理解，是按给定N和k之后m的置信区间反推N的置信区间的。而且似乎假设了序号在1~N中为连续的实数分布。最终的结果，概率为r的置信区间是[m/q^{1/k}, m/p^{1/k}]，其中p=(1-r)/2，q=(1+r)/2。

我觉得既然m的分布式都有了，感觉可以直接通过分布式求出置信区间啊。而且如果想求0%置信区间就会发现问题：得到的区间这时是一个点，这个点与无偏估计不同，那这个点的值是什么意思呢。。

2. 贝叶斯学派

Bayes学派的解释就清晰多了，但丫需要先对N的先验概率分布进行假设，但现在我们对N没有任何先验知识，最幸福的当然是假设一个在所有自然数上的均匀分布，但这样会导致每个点概率都是0，所以采用的方法是假设N有一个最大值\Omega，这样用Bayes公式就可以方便的进行估计，得到给定m，k的情况下，N的概率分布，式子是这个：

http://upload.wikimedia.org/math/c/2/1/c216132e1658067282cb08e2b43ef6ea.png

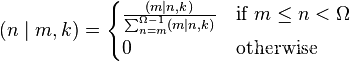
注意这个式子里是用的n代替本文中的N。

如果在\Omega趋于无穷时上式的分母有限，可以去掉这个讨厌的\Omega，这样就幸福了。。但没有给出什么时候这个条件可以满足。。

几个简单的结论：所有数值中，概率最大的N的值（众数）为m，只有当k>=3时，N有有限的数学期望(m-1)(k-1)/(k-2)，k>=4时N有有限的方差。

对原始问题的一些讨论：

1. 总之觉得频率学派的计算和解释不好理解，因为我对频率分析的方法不够熟悉，而在我的知识体系里面，Bayes的推导非常靠谱。但当k=1时，频率学派可以给出一个很Reasonable的解为2m-1，而Bayes方法没有\Omega的话N的期望是无穷大。。

2. 重新写一下频率学派的无偏估计：N=m-1+m/k，Bayes的数学期望：N=m-1+(m-1)/(k-2)，两个式子只差最后一项，注意m一定大于k，所以m/k>1/2，所以Bayes的结果会较大，如果观测点的数目k越来最多，m也会越来越大，两者的值就很接近了。

3. 看起来两种方法的推导都是对的啊，为啥得到的结果会不一样呢？是因为求的东西不一样。频率学派是假设给定N，求m的数学期望，“无偏估计”是指在N确定的情况下，多次进行观测实验，对结果进行估计，得到的结果的数学期望就是真实值N；Bayes学派是认为观测m确定，求N的概率分布。

4. 等一下。。。上一条的解释里为什么没有提到k？m和k都是已知的一部分，数学上是两个地位等同的变量啊？再重新看看上一条的解释，如果把上一条中的"m"替换为"m和k"，对于Bayes学派来说仍然说得通，但是频率学派就有问题了：为什么没有求k的数学期望呢？上面说的“多次进行实验”是在k和N确定的情况下进行实验的，为什么k要确定呢？Things are getting a little interesting ... 试试把频率学派推导中的m和k交换一下，第一步要求m和N确定情况下k的概率P(k|N,m)，发现求不出来。。因为没有k的先验。。那为啥P(m|N,k)就可以求呢？为啥m就不需要先验呢？因为有了N和k，m的分布就唯一确定了，但是有了N和m，k的分布却无法知道。所以在频率学派的解释里，k和N被认为是确定的模型参数而非随机变量，而m是每次观测得到的随机变量。“无偏估计”是按每次观测m来说的。

5. 事情还没完。。。那按上面的解释，从频率学派的角度来讲，数学上N和k的地位就可以交换了，于是我们的问题如果换成：已知所有坦克的数量N和观测到的最大值m，估计观测的次数k。频率学派的解法应该是类似的。尝试解了一下，按原来的方法强制代入是可以求出估计值的：k=m/(N-m+1)，但这感觉应该不是无偏估计，因为k和m的关系是非线性的。按频率学派的思想求解k的最小方差的无偏估计，直观感觉可做，但应该会比较麻烦。而反过来，如果Bayes学派来回答这个问题，需要假设k的先验，按定义域最简单的应该是[1,m]这个区间内自然数上的均匀分布（但这听起来也不合理啊）。

二、频率学派与Bayes学派

这个问题的确可以反映出两者的很多区别，翻了翻一些相关的资料总结一下我的理解：

1. 可以把所有已知的未知的数值分成两部分，一部分是模型参数，一部分是观测到的数据。频率学派认为，模型参数是客观存在的，固定的，比如“火星上是否有生命”，要么有要么没有，只是我们不知道而已，而观测到的数据是在确定的模型参数下依模型决定的分布进行采样的结果。而Bayes学派认为参数也是随机变量，所以需要参数的先验分布，也就是人们对参数的先验知识，但有时这个先验分布本身又是带参数的，这些参数就是“超参数”了，这样有可能会有多层到"超超..参数"，比如LDA的各种变种，但最上层的参数我们仍然会认为是确定的，或者说，给一个确定的分布形式。

2. 看起来，如果把Bayes中最上层的“超参数”理解成模型参数的话，两者不就一样了？不是的，世界观的不同造成了方法论上的区别（这话还是很有道理的。。。），首先通常不会有频率学派的方法引入超参数，这本来就是个Bayes理论里的概念啊。。其次，频率学派更注重“点估计”（point estimation），得到一个待求参数的数值（无偏估计或MVUE），Bayes学派则会得到一个待求参数的分布，再计算期望方差什么的。对应的，频率学派可以用置信区间描述估计的准确程度，置信区间大约意思是这个确定的真实模型参数以概率r（比如95%）落入的区间范围。

3. 似乎从前频率学派是非常流行的，但慢慢Bayes学派在有方便描述的先验的领域取得了非常好的效果，方便引入domain knowledge，逐渐占了上风（这个理解可能会有偏颇）。

4. 似乎在概率推导时采用Bayes学派思想的很多，但evaluation中经常用到频率学派的置信区间，假设检验的计算方法。

参考文献：

英文：

http://oikosjournal.wordpress.com/2011/10/11/frequentist-vs-bayesian-statistics-resources-to-help-you-choose/

http://www.stat.ufl.edu/~casella/Talks/BayesRefresher.pdf

xkcd: Frequentists vs. Bayesians (这只是个搞笑漫画而已。。。)

中文：

为了大一统的大一统？贝叶斯与频率学派的永久之战 - Yihui Xie | 谢益辉

http://www.douban.com/group/topic/16719644/

三、原始问题的变化

一边看一边想到的。

1. 在坦克问题里观测到的序号是不会重复的，坦克被俘了就没了，下一次不会看到同样的坦克，如果每次记下序号之后再放回去（蛋疼。。。），也就是观测到的序号可以重复，结果会是如何？

不管对什么学派，都要把P(m|N,k)改为P(m|N,k)=(p(m,k)-p(m-1,k))/p(N,k)，这里p(x,y)为x中取y的排列数，用小写p与大写P的概率区分。后面的做法应该是相似的。

2. 如果在上面1的基础上，已知k次观测中每次观测得到的序号从小到大为m_1, ..., m_k（于是m_k就是原始问题中的m），结果会是如何？

情况又有点不一样了。。对于Bayes学派，后验概率为：当N>=m_k时，P(N|.)正比于1/N^k，N取其他值时为0，于是N的众数为m_k，k<=2时数学期望无穷大，k>2时有有限的数学期望，没仔细算，但这个数学期望（形式非常简单，一个求和除以一个求和）很可能和原来不一样，因为N的分布和原来不一样。这个期望有时为超越数，参见：

http://en.wikipedia.org/wiki/Riemann_zeta_function

对于频率学派，我不会做。。。

3. 在What If有一个相关的更有趣的Twitter时间线长度问题，中文版：

http://select.yeeyan.org/view/235419/380693

What If英文原版：

http://what-if.xkcd.com/65/

==============

zhangtianrong2.docx (live.com)

概率—德国坦克问题和贝叶斯分析

作者：张天蓉

现代人的言语中，越来越多地提到“概率”一词。人们用概率来度量事件的不确定性，比如抛硬币掷骰子之类的游戏，其结果是不确定的，被称为随机变量。概率论便是研究随机变量变化规律的科学。法国著名物理学家拉普拉斯（1749年-1827年）曾经如此评论概率论：“这门源自赌博机运之科学，必将成为人类知识中最重要的一部分，生活中大多数问题，都将只是概率的问题。”

两百多年之后的当今文明社会，证实了拉普拉斯的预言。概率及统计学的一些基本概念，已经悄悄地渗透到人们的工作和生活当中，小到人人都可以买到的彩票，大到如今热度不减的各种大数据，还有近年来突飞猛进的人工智能技术，包括打败人类顶级围棋手的“阿尔法狗”和自动车辆使用的“深度机器学习”算法，都与概率及统计密切相关。

因此，人人都有必要学点概率和统计。本文的目的旨在介绍一个在现代概率统计及其应用中颇为重要的贝叶斯学派，其分析方法构成当今人工智能中常用的机器学习之基础框架。

我们的故事，从第二次世界大战中的德国坦克问题讲起……

德国坦克问题

当年，德国佬正在大规模地生产坦克，盟军想要知道他们每个月的坦克产量数。为了了解这个信息，盟军采取了两种方法：一是根据情报人员刺探的消息而得到，另一种是根据盟军发现和截获的德国坦克数据，用统计分析办法得到。根据第一种方法得到的情报，德军坦克每个月的产量大约有1400辆，但根据概率统计推断的方法，预计的数量只有数百辆。二战之后，盟军对德国的坦克生产记录进行了检查，发现统计方法预测的答案（见表1）令人惊讶地与事实符合【1】，统计学家们是怎么做到这点的呢？

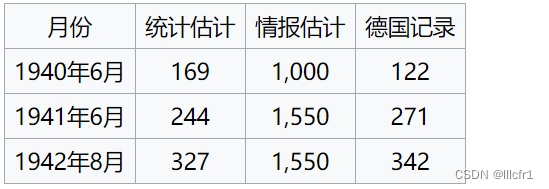
     表1（来自维基百科）

那时候，德国制造的每一辆坦克上都有一个序列号。假设德国每个月生产一批坦克，从1到最大值N顺序排列，因此，可以把这个最大编号N，当作每个月总的生产量。盟军发现和截获的任何德国坦克上的序列号，都应该是介于1和N之间的一个整数，根据这些截获坦克序列号的数据，如何来猜测总的生产数N？这是当年的战争给数学家们提出的难题。

这是一个统计推断的问题，也就是从观察到的数据样本（序列号），来推断随机变量的某些整体参数（N）。如今思考这个问题，有两种不同的推断方法：经典方法和贝叶斯推断。

经典统计推断包括几个基本原则：最大似然（概率）估计、最小方差、无偏性等等。简单而言，经典统计使用求极值的方法，让选取的某个似然函数最大化，同时也考虑样本平均平方差最小化，而无偏性指的则是尽量使得样本平均值等于整体平均值。

比如说，先考虑最简单的情况：在某个月内，盟军只发现了1辆德国坦克，其标号为60，那么，你如何来估计德国在这个月生产坦克的总数N？也许读者会说：“你疯了！只有这么1个数据，有什么可估计的？还能使用什么统计方法吗？参数N是任何数值都有可能的，只能随便猜测一个啦！”

不过，你的说法显然不正确。首先，N不可能是任何数，N的值起码要大于或等于60！严肃的统计学家就更不会这么说了，即使对如此少量的数据，他仍然可以进行他的统计推断。

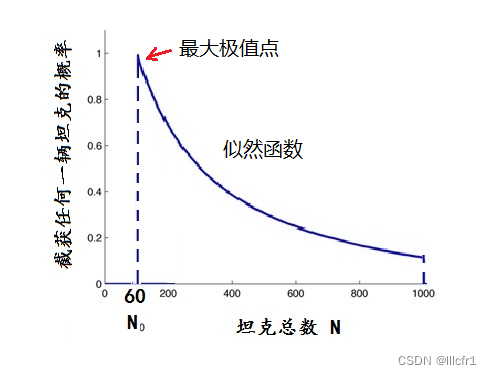
图1：截获任何一辆坦克的概率vs坦克总数

第一，为了估计真实的总产量数N0，他需要构造一个概率函数，称其为似然函数。设想：如果这批坦克生产的总数是N的话，根据等概率原则，拦截到1到N中任何一个编号的坦克的可能性都相同，均为1/N。也就是说，截获任一辆坦克的概率是坦克总数N的函数：N越大，即生产的坦克数越多，截获某个编号坦克的概率便越小。概率随N的变化情形，如图1所示的一截双曲线。这个概率分布曲线，便可选作似然函数。

最大似然估计的目标是找出概率最大的点对应的N0，因为这个问题中，N越小概率越大，所以得到在最大化概率点的N0=60，即图中曲线最左边的起始点。

经典方法的第二个考虑是最小化均方差（MSE）。为此，我们假设总产量N不是刚好等于60，而是乘以一个大于1的因子a。想象盟军看到了N个坦克中所有的坦克，那么，均方差可以按照如下方法计算并最优化，再求最小值。

图2：将均方差最小化

从上面的计算结果，当坦克总数N比较大时，相乘的因子a近似为3/2，由此可将N0的估计值从60，调节到N0 (均方差最小) = 60×3/2 = 90。

最后，还得考虑样本的无偏性。如果N0=60的话，这个样本太不符合“无偏”的条件了，既然每一辆坦克被发现的概率都是一样的，凭什么盟军截获了一辆坦克就截到了最后生产的那一辆呢？这听起来太奇怪了，N0=90也不符合无偏，最符合无偏条件的就是截获的是序号为中间的那一辆，它的序号使得样本序号的平均值等于整体所有样本序号的平均值。也就是说，无偏的N0被估计为60的两倍，N0 (无偏)=120.

真不愧为数学家，仅仅截获到1辆坦克，就有这么多的考虑，如果截获了更多呢？我们可以将问题一般化，以上经典学派的思考方式也可以推广到一般的情况，简单叙述如下：

问题：盟军发现了k辆坦克，序号分别为i1……ik，最大的序号是m，估计总数N0。

经典推断方法的答案：N0 = m + (m-k)/k。

比如说，盟军发现了5辆坦克，其序列号分别为215、90、256、248、60，因此，k = 5，m = 256。从以上经典方法的公式，得到坦克未知的总数N0 = 256 +（256-5）/5 = 306。

以上使用的是经典统计推断方法，但实际上，概率统计中有两大主要派别，经典学派也被称为频率学派，另一派则被称为贝叶斯学派，贝叶斯学派又如何解决德国坦克问题呢？

贝叶斯派的估算方法比频率派的方法更为有趣和更有意思。贝叶斯派有别于频率派的重要差别之一就是对“参数”的看法。频率派认为任何系统的物理参数是固定不变的客观存在，比如这儿的参数N，经典方法的目的是要找出这个N。而按照贝叶斯派的观点，物理参数不一定是固定的，对外部观察者而言，它们也可以被认为是随机变量。因此，统计推断方法企图追踪的不是模型参数N本身，而是参数N取各种可能值的分布情况。贝叶斯派解决坦克问题的思想是：未知欲求的生产量N是一个服从某种概率分布的随机变量。随着数据样本的增加，N的概率分布函数不断被更新，贝叶斯推断描述这个更新的过程。

以刚才截获5辆坦克的具体数据，来说明贝叶斯派的推断过程。

假设盟军截获的第一辆坦克序列号是215，从前面频率派方法最开始的一段分析可知，对应这1个样本，N可能是从215开始的任何整数，但是，N值越大，概率越小，我们暂时忽略N值大于1000的情况，可以画出N的概率分布是类似于图1的双曲线，不同的是曲线的起始点和形状，图1中的曲线参数N0=60，这儿的参数N0=215，见图2a中最大值在N0=215处的“序列号215分布”曲线（蓝色）。

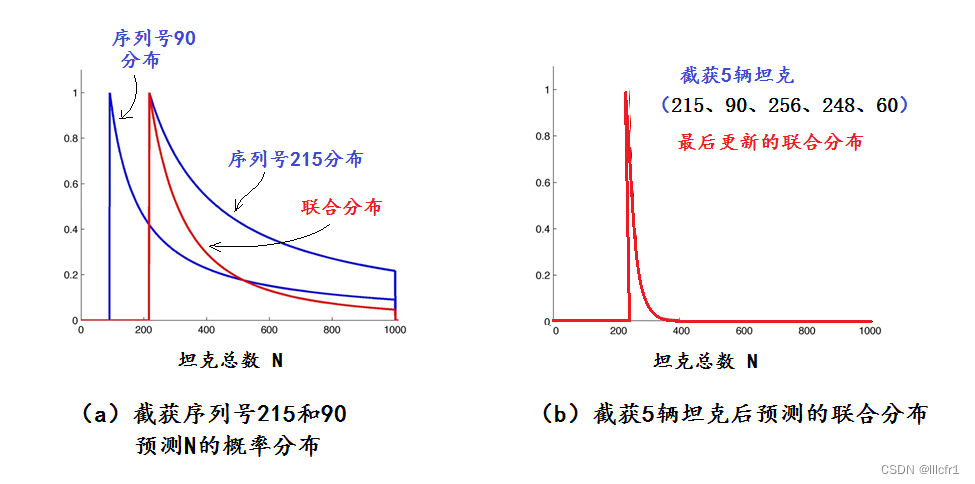
图2：贝叶斯推断解决德国坦克问题

现在，我们加上第二辆坦克的信息：序列号90。因为90小于215，它的出现并不改变似然函数的最大值，但是它却对N的分布曲线有所影响，两个变量的联合分布曲线用图2a中的红线表示，这也是加上第二个数据之后更新了的参数分布。如图可见，序列号90的数据使得概率分布曲线变得更尖锐，说明N的较大数值出现的概率大大降低。

如果再加上后面3个样本：序列号256、248、60，五个样本的联合分布变得更为尖锐，峰值是256，N=400到1000的概率已经几乎为0，可以忽略不计了，如图2b所示。

在这个具体例子中，最后对N0的估计：频率派的N0 = 306，与贝叶斯派的N0 = 256相差不大，难分孰优孰劣。然而，通过该问题，我们简单了解了频率派和贝叶斯派的不同思考方法。概率统计中这两大学派的争论由来已久，既涉及哲学观念，也有关计算方法，由于历史的原因，概率及统计的教科书，基本上是以频率学派为主流观点而写成的。尽管目前贝叶斯概率已成为一个热门研究课题，在机器学习以及物理、医疗等领域都有应用，但一般非专业人士对贝叶斯派的观念和方法并不熟悉，因而笔者在下文中略加介绍。

概率是什么？如何定义概率？

首先，我们简单总结频率学派与贝叶斯学派的差异，可归结为对如下两类问题的不同答案：

一、概率是什么？如何定义概率？概率是主观的，还是客观的？

二、如何看待和使用概率统计模型中的参数？参数是客观而固定的吗？

第一类问题看起来涉及的是两派观点的哲学层面，后面一类问题有关具体计算方法。但两者互相关联，因为看待世界的观点不一样，所以企图用以描述世界的计算方法也有所不同。

概率是什么？如何定义？从历史的角度看，概率起源于抛硬币掷骰子之类的赌博游戏，因此，概率最早便被定义为多次试验中某随机事件出现的频率之极限。事件出现的频率又是什么呢？是事件发生的次数与总次数的比值。例如，抛硬币10次，正面出现了6次，我们说：出现正面的频率为0.6；抛硬币20次，正面出现了11次，那么，出现正面的频率为11/20=0.55……，如此继续下去，抛硬币次数不断增加后，频率值趋近的极限便是出现正面的概率。如此定义的概率，被认为是频率学派的观点。

然而，如上定义的概率，只能代表我们使用这个名词的情况之一。有很多时候，概率无法用多次试验来得到，比如说，人们可以估计某一天北京下雨的概率，但这是无法进行试验的；又比如，加州某年某月某日地震的概率，也无法用多次重复来验证。又比如说，某个国家研制的导弹，如果谈到命中1000公里之外目标的概率，在原则上是可以用重复试验来估计和证明，但事实上却绝对不会这样做，因为花费实在太昂贵了。

从上面所举的几个实例可见，很多时候，概率一词所描述的并不是“对随机事件重复频率”之极限，而更应该被表述为对某种“不确定性” 的度量。

无论何种定义，一个事件的概率值通常都以一个介于0到1之间的实数表示。如果说它是对随机事件发生之可能性的度量，那么，不可能发生事件的概率为0，确定发生事件之概率为1，而大多数实际事件的概率值是0与1之间的某个数，这个数代表事件在“不可能”与“确定”之间的相对位置。事件的概率值越接近1，事件发生的机会就越高。

由于对概率定义的差异及哲学上的分歧，另一种概率统计的派别，即贝叶斯学派逐渐兴起，两派之争一直贯穿于概率及统计发展的历史中。

贝叶斯和贝叶斯定理

托马斯·贝叶斯何许人也？他是18世纪英国的一名统计学家（Thomas Bayes ，1701年–1761年），曾经是个牧师，喜欢研究数学。他对概率论和统计学作出的最大贡献是贝叶斯定理。

当年，贝叶斯研究一个“白球黑球”的概率问题。概率问题可以正向计算，也能反推回去。例如，盒子里有10个球，黑白两种颜色。如果我们知道10个球中5白5黑，那么，如果我问你，从中随机取出一个球，这个球是黑球的概率是多大？问题不难回答，当然是50%！如果10个球是6白4黑呢？取出一个球为黑的概率应该是40%。再考虑复杂一点的情形：如果10个球中2白8黑，现在随机取2个球，得到1黑1白的概率是多少呢？10个球取出2个的可能性总数为10*9=90种，1黑1白的情况有16种，所求概率为16/90，约等于17.5%。因此，只需进行一些简单的排列组合运算，我们可以在10个球的各种分布情形下，计算取出n个球而其中m个是黑球的概率。这些都是正向计算的例子。

不过，当年的贝叶斯更感兴趣的是反过来的“逆概率问题”：假设我们预先并不知道盒子里黑球白球数目的比例，只知道总共是10个球，那么，比如说，我随机地拿出3个球，发现是2黑1白。逆概率问题则是要从这个试验样本（2黑1白），猜测盒子里白球黑球的比例。

读到这儿，你会发现贝叶斯研究的逆概率问题与本文开始所介绍的德国坦克问题有些相似之处：它们都是企图从样本数据来猜测和推断某些物理参数。德国坦克问题中需要猜测的是总产量数N0，上文中的黑白球问题，未知待定的是盒子里白球黑球的比例。

为了解决此类问题，贝叶斯在他的论文中提供了一种方法，即贝叶斯定理：

后验概率 = 观测数据决定的调整因子×先验概率 

上述公式的意义，指的是对未知概率首先有一个先验猜测，然后结合观测数据，修正先验，得到更为合理的后验概率。“先验”和“后验”是相对而言的，前一次算出的后验概率，可作为后一次的先验概率，再与新的观察数据相结合，得到新的后验概率。此外，公式中的先验概率和后验概率，也不一定是指一个概率值，而可以是对应于某些物理参数的概率分布。因此，可以运用贝叶斯公式来推断未知的概率模型参数，并根据新的观测数据对模型参数逐次修正并得到最终结果，解决逆概率（或统计推断）问题。本文一开始所介绍的德国坦克问题中，贝叶斯派便是使用贝叶斯定理来逐步更新N的概率分布函数。

有关贝叶斯定理的论文，直到贝叶斯死后的1763年，才由朋友代为发表。后来，拉普拉斯证明了贝叶斯定理的更普遍的版本，并将之用于天体力学和医学统计中。

也许贝叶斯当初对他自己这个定理的意义认识不足，也万万没有料到由此定理而启发人们以一种全新的思考方式来看待概率和统计，并继而发展成所谓“贝叶斯学派”【2】。

如上所述，使用贝叶斯定理，能用少量的观测数据，逐次修正而得到模型参数。这种方法与频率学派那种进行大量实验而得到结果的方法，是完全不同的两种思维模式。

在历史上，贝叶斯统计长期受到排斥，受到当时主流的数学家们的拒绝。然而，随着科学的进步，贝叶斯统计在实际应用上取得的成功慢慢改变了人们的观点。贝叶斯统计慢慢地受到人们的重视，人们认为它的思路更为符合科学研究的过程以及人脑的思维模式。

贝叶斯分析方法长期受人诟病的另一个原因，是对概率之本质的理解：根据频率学派的观点，概率（或者决定概率的物理参数）是客观存在的，不以人类的主观判断为转移。而在贝叶斯派的方法中却涉及到一个需要人为猜测的“先验概率”，将概率看成对某个命题的“主观信任度”。那么，概率到底是主观的还是客观的呢？这又是一个与哲学相关的问题。

主观和客观

传统的科学家们，一贯认为他们所研究的对象是客观存在的，如果谈到某个物理系统的“参数”，那应该是一些描述该系统的固定物理量。比如我们可以具体举硬币的例子说明之。一个硬币也许是一枚两面对称的公平硬币，也许是一枚有偏向性的硬币，它的偏向性可以用一个参数p来表示：对公平硬币，p=0.5；如果两面重量非常不均匀，出现正面的概率可能大大地大于反面，比如说p=0.8、0.9等等。但是无论如何，这个表征偏向性的参数p是在铸造硬币时就被决定了的一个不变物理量，我们翻来覆去地不停抛丢这枚硬币，就可以逐渐确定p的数值。因此，频率派学者认为：概率是客观的，由客观存在的一些固定物理参数所决定。

以上说法言之有理，但并不是对任何情况都适用。比如在某次总统选举中，有评论文章说某候选人获胜的概率是75%，另一位只有25%，这个例子中，就很难找到任何客观固定的物理本质与这种说法相对应起来了。

也就是说，虽然有时候概率确实能够通过大量重复实验获取的频率测得，但是这并非概率的本质。因此，贝叶斯理论认为，概率的概念应该被扩展为对一个命题信任的程度，有人便针对频率派认定的“客观概率”，提出了主观概率的概念。

图3：贝叶斯和拉姆齐

英国数学家及哲学家弗兰克·拉姆齐（Frank Ramsey，1903年－1930年）在他1926年的论文中【3】首次建议将主观置信度作为概率的一种解释，他认为这种解释可以作为对频率派概率的客观解释的一个补充或代替。

主观、客观的观念属于哲学范畴，主观指与人有关的意识、思想、认识等，客观，指人的意识之外的物质世界或认识对象，主观和客观的关系问题，是认识论中的基本问题。

许多决策问题的概率不能通过随机试验去确定，那就只能由决策人根据他们自己对事件的了解去设定。这样设定的概率反映了决策人对事件掌握的知识所建立起来的信念，称为主观概率，以区别于通过随机试验所确定的客观概率。因此，概率的客观性指的是它独立于任何使用者，仅由物理参数而决定的个性。

可以举出很多概率具有主观性的例子，比如以赛马为例，大多数观众并不具备对马匹和骑师等因素的全面知识，而只是凭主观因素对赛马结果下赌注，他们认可的某个马匹的获胜概率反映的是他们的个人信念，不一定符合客观事实，因而是主观概率。另一个例子：地震研究者预测某地区某月是否发生6级地震的概率，除了该地区的客观地层情况之外，还可以参考许多年的历史记录，也有与该研究者有关的许多“主观”因素参与其中。另外，美军某月某日于某处抓到本拉登的概率，有少量客观情况，更大程度上是依靠主观臆测。

概率到底是客观的还是主观的呢？概率到底从何而来？概率的物理本质是什么？这些问题既是哲学的，也是物理的，因为它们的答案实际上也取决于产生概率的物理系统的本质：是前述的硬币具有的那一类固定参数体系，还是未知的、甚至不可知的系统。

概率既反映客观事实，也有主观因素。就两派观点而论，频率学派强调概率的客观性，贝叶斯派更重视其主观因素。频率派认为概率是事件在长时间内发生的频率。对许多事件来说，这样解释概率是符合逻辑的，但对某些没有长期频率的事件来说，这样的解释便显得难以理解。因此，贝叶斯派把概率解释成是对事件发生的信心，是观点的概述，是对不确定性的主观置信度。

有趣的是，每个人都可以给某个事件赋于概率值，因此，主观概率不是唯一的，而是因人而异。这点也与现实吻合，反映了不同的人对同一事件拥有的信息不同，思维方式不同，因此而对该事件是否发生的信任度也不同。但这些不同一般不能仅仅用非黑即白的简单“对错”来描述，这也是物理世界的现实。

然而，有人由此而责难主观概率派，认为不符合唯物主义，远离了科学研究的宗旨。概率应该是对客观世界本质属性的一种描述，应该独立于主观意识而存在，怎么会是主观的且因人而异呢？事实上，承认主观概率，并不代表唯心主义，而是更为准确地描述人们在科学活动中的实验和更新理论的思维过程。

科学毕竟有别于哲学，即使认同物理世界是客观存在的，解决问题的科学方法却总是人为的，难免掺进主观的因素，自觉或不自觉地，明显的或隐含的，不管哪个派别，主观性都在所难免。作为数学的应用，必须具体问题具体分析，哪种方法有效便使用哪一种，主观还是客观之说法，只不过是凌驾于科学之上的“哲人”们对理论的不同诠释，对解决具体问题无济于事。

某些学者并不认为两大学派的区别是在于对概率的不同定义，现在的频率学派也同意应该将概率定义为对不确定性的度量，只不过，频率派与贝叶斯派探讨“不确定性”的出发点与立足点不同。这来源于他们看待“参数”的观点不同。

频率学派试图直接为产生“事件”的物理本质，即固定的“参数”建立模型，比如他们主张不断地抛掷硬币，便是企图想要从抛掷次数增大时正面朝上次数的变化，来得到反映硬币正反偏向性的物理参数p。

而贝叶斯学派认为，也许根本不存在这个固定的物理参数p，反之，数据是比“物理本体”更为重要的真实存在，人们只能通过“观察者”得到的数据来进行猜测和推断。所以，他们不为“参数”建模，而是企图为 “猜想推断”过程中数据的变化建模，其建模方法便是使用贝叶斯公式将模型参数之分布情况不断更新，因为在贝叶斯派的眼里，参数不是固定的，也是一个具有概率分布的随机变量。

换言之，频率学派试图描述的是事物本体，而贝叶斯学派试图描述的是观察者知识状态在新的观测发生后如何更新。世界观的差异影响到他们方法上的差异。频率学派更为强调“多次试验”，贝叶斯学派则强调探索更新结果的方法。

和谐共处、求同存异？

更为有趣的是，还有人用玩麻将游戏为例来比喻频率派和贝叶斯派。如果你在游戏中，只考虑下面未翻开的牌中还剩下些什么，并且根据计算这些牌下次出现的概率来作决定的话，那你就是个频率学派。而贝叶斯派打麻将时的考虑要复杂一点：不仅仅要记住下面有什么牌，还得看游戏的过程中谁打了些什么牌？什么时候打的？因为除了桌子上剩下未翻开的牌之外，还有在各人手中的牌也是未知的，对于这些未知的情况你只能作猜测，并且，每个人打牌的方式不完全相同，这是人的主观性。每个人手上的牌也不是固定的，是随着游戏的进展，根据场上的情况而变化的。因此，你摸到某张牌的概率不固定，也在不断地变化，你需要根据场上情况的变化，不断地更新你有关“牌局”的知识而做出决断，大多数麻将高手可能都是这么做的。便有人开玩笑说：麻将高手们都可算是贝叶斯派哦！

以上的说法也表明，贝叶斯派的思考方法更为自然，更符合人们大脑的思维方式。贝叶斯推断是通过新得到的证据不断地更新你的信念，一旦你的信念被更新，你能根据更新的知识做出可信的判断，但贝叶斯主义很少做出绝对性的判断，总是会保留一定的不确定性，生活中的实际情况也是如此。无论从打麻将还是玩扑克牌的游戏中，大家都能体会到，不确定的因素太多了，这些不确定来自于“牌”混合之后的客观分布，也来自于所有游戏参与者主观的思考、方法和判断，并不是一个仅仅靠逻辑推理就能决定输赢的过程。

不少人认为贝叶斯分析的方式和人脑的工作机制有相似之处，这也是为什么近年来将贝叶斯统计方法广泛应用于人工智能研究，特别是机器学习领域的原因之一。当今人工智能技术的崛起，部分归功于计算和统计的联姻，实际上也就是计算机和贝叶斯方法的联姻。

按照如上说法，贝叶斯派好像不错，那么，频率派的观点和方法是否应该被抛弃呢？

不是。频率派的方法仍然非常有用，在很多领域可能还是最好的办法。再则，如果一切都只从贝叶斯的观点出发，很多理论分析会陷入困境。比如重要的大数定律和中心极限定理，这两个概率论的基本原理，都是基于频率派多次试验的基础上。

尽管两学派的世界观不同，各有其信仰、内在逻辑、解释力和局限性，但在实用上仍然可以把两个派别的方法结合起来，两个学派的统计学家基本上都承认大数定律和中心极限定理，也都使用贝叶斯公式。不过两派学者使用这些定理的方式和场合不完全一样而已。两个派别从两种不同的哲学观来诠释各种统计模型。在一段不短的时期内，频率派和贝叶斯派也许将继续在观念上争论不休，但在具体计算时，却会互相取长补短、求同存异。

参考文献：

【1】Ruggles, R.; Brodie, H. (1947). "An Empirical Approach to Economic Intelligence in World War II".[J],  Journal of the American Statistical Association. 42 (237): 72.

【2】Edwin Thompson Jaynes. Probability Theory: The Logic of Science.[M], Cambridge University Press, (2003).

【3】Frank P. Ramsey (1926). "Foundations of Mathematics". Proc. London Math. Soc. 25: 338—384.