Neural Networks and Deep Learning 学习笔记(二)

1. 第一章习题解答。

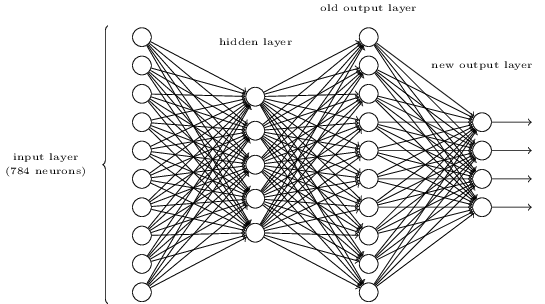
There is a way of determining the bitwise representation of a digit by adding an extra layer to the three-layer network above. The extra layer converts the output from the previous layer into a binary representation, as illustrated in the figure below. Find a set of weights and biases for the new output layer. Assume that the first 3 layers of neurons are such that the correct output in the third layer (i.e., the old output layer) has activation at least 0.99, and incorrect outputs have activation less than 0.01.

假设新输出层从上到下依次为高位到低位。

十进制与二进制对照表：

0	1	2	3	4	5	6	7	8	9
0000	0001	0010	0011	0100	0101	0110	0111	1000	1001
null	0	1	0、1	2	0、2	1、 2	0、 1、 2	3	0、 3

output neuron对应的是：

最高位	第二位	第一位	最低位
8、9	4、5、6、7	2、3、6、7	1、3、5、7、9

用i代表原始输出从上到下的次序，用j代表输出的nybble从上到下的次序，$W_{i j}$指的就是，第i个原始输出进入最终输出的第j个时的权重。如果把每个神经元比作一个灯泡，如果原始输出第7个（从第0个开始数）亮了，那么最终输出的第0和1和2个就会亮；原始输出第8个亮了，那么最终输出的第3个灯泡就会亮。也就是说，对于原始输出的7，它输出有四条线，分别连到最终输出神经元的0~3，其中有三条，即第0、1、2条的weight为10（权重大小随便定的），第3条为-10，这样，当7亮时，最终输出的神经元即0、1、2号一定会亮。因为影响最终输出的0号神经元（代表最低位）的有10条，但是，7亮时，其它是不亮的，而$w_i \cdot a_i$中，不管别的$w_i$是不是10，$a_i$总是0，所以即便最终输出的0号神经元有10条输入的线，其中8条权重是10，但最终输出的0号神经元还是只受7号线影响。

反过来，如果最终输出的神经元的第3位亮了，剩下的都没亮，则可以看到，可能的输入是8、9，而第0位没有亮，所以不可能是9，结果是8。

对了，那个bias……这边用不到。

附个stackoverflow的解答连接
stackoverflow解答链接