本周课程主要内容有:
- 高斯消元法及其应用;
- 内积定义与正交基础。
在前面章节的算法练习中,我们使用 solver 模块求解线性方程的解,那么,该模块是如何实现的呢?
首先介绍高斯消元法(Gaussian elimination),它的应用场合有:
- 寻找给定向量跨度(Span)的基底。这一应用同时可以提供求秩以及判定线性相关性的算法。
- 求解矩阵方程,等同于将一个给定向量表示为其它给定向量的线性组合形式,也等同于求解一个线性系统的方程。
- 寻找矩阵零空间的基底,等价于寻找齐次线性系统解集的基底,对一般线性系统解集的表示同样有着重要的作用。
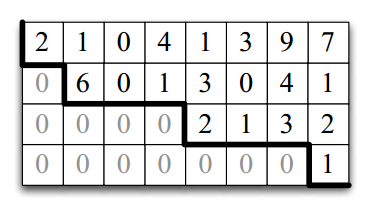
高斯消元法主要是为了将矩阵化为梯阵式的,所以,在介绍高斯消元法之前,首先要了解梯阵式(Echelon form),它是三角矩阵的一般化形式,定义为:如果一个 m * n 矩阵满足下面条件,就成它是梯阵式矩阵:对任意行,如果这一行的第一个非零入口的位置为 k ,那么前面每一行的第一个非零入口的位置都小于 k 。下面矩阵就是梯阵式矩阵:
那么,如果一个矩阵是梯阵式的,会带来什么好处呢?
引理:如果一个矩阵是梯阵式的,那么非零行将构成行空间的基底。
通过上面引理,提出一种求解矩阵 A 的 行空间基底的方法:
迭代变换 A 为 B :
- B 是梯阵式的;
- B 的行空间与 A 相同。
通过不断的尝试,我们得到了一个实现这一目标的算法:
下图演示了通过该算法实现的矩阵的变换过程:
在算法推导过程中,用到了一个重要的定理:如果 MA = B 且有 M 是可逆的,则有 Row A = Row B。
在变换过程中用于将同列其它元素消零的元素称为主元素(Pivot element)。
可以证明,上面算法在数学上是正确的,但是由于在实际应用过程中,采用的是浮点运算,存在舍入误差,这样就导致了高斯消元法在变换过程中会出现错误。
通过采取一定的技术手段可以减轻出错的可能性,本课程不做进一步介绍,只将该算法应用于 GF2 域,关于实数域的改进有兴趣的读者可以自行查阅相关资料。
前面说过,利用高斯消元法可以求解线性系统的解,以及寻找矩阵的零空间,实现这两种想法的关键在于:记录将矩阵化为梯阵式时的变换过程。
下面是实现这一想法的描述
给定矩阵 A ,求矩阵 M 和 U 使得 MU = A ,其中
- U 是梯阵式的;
- M 是可逆矩阵。
这样,欲求解线性方程 Ax = b:
- 计算 M 和 U 使得 MU = A ;
- 计算矩阵向量乘积 Mb ,求解线性方程 Ux = Mb
上面的解即是方程 Ax = b 的解。
那么如何求解 Ux = Mb 呢?
- 如果 U 三角阵(Triangular),可以使用前面章节介绍的反向迭代算法(Back-substitution);
- 一般情况下,可以使用类似的算法。
至于在求解矩阵零空间方面的应用,对于上面的 A ,我们不直接寻找它的零空间,转而寻找它的转置 A^T 的零空间的基底,即 {u:u * A = 0} 的基底。
举个例子,如下图所示:
U 最后两行为零向量,它们分别由 M 的最后两行乘以 A 求得,数学上,我们可以证明, M 最后两行构成 Null A^T的一组基底。
修改一下前面的算法,可以令其返回对应的变换矩阵 M ,算法描述如下:
这里再强调一下,由于浮点运算的舍入问题,高斯消元法不能直接用于求解实数域上的相关问题,但是对于 GF2 上的问题则是可以胜任的。
对于实数域上的问题,可以通过正交化进行求解,下面介绍内积和有关正交的基础知识,正交化的详细描述将在下周介绍。
我们定义两个向量 p 和 q 的距离(Distance)为它们的差p -q的长度,这意味着我们需要定义一个向量的长度(Length),事实上,我们并不在向量中使用长度这样的说法,而是将其称为向量的模(Norm),表示为 ||v || 。
向量的模具有下列性质:
- 性质一:|| v || 是一个非零实数。
- 性质二:当且仅当v 是零向量时,||v || = 0 。
- 性质三:对于任意的标量 alpha ,有 || alpha *v || = alpha * ||v || 。
- 性质四:||u +v || <= ||u || + ||v || 。
一种定义向量的模的方法是定义向量的一种称为内积的运算。
向量 u 和 v 的内积表示为 <u,v > 。
这里需要声明的是,没有定义 GF2 域上的内积的方法。
对于实数和复数,在内积的定义上存在一定的灵活性,这种灵活性在机器学习中体现的尤为明显。
一旦我们定义了内积向量 v 的模可以定义为
对实数域上的姓梁,我们定义内积为点乘,即
不加声明,后面有关内积的描述均是针对实数域上的向量。
内积具有下面三个性质:
- 第一个参数上线性:

- 对称性:

- 齐次性:

正交(Orthogonality)是线性代数中对于垂直的表述,定义为:如果 <u, v> = 0 ,则称向量 u 和 v 是正交的。
正交具有下列性质:
- 如果 u 正交于 v ,则对于任意标量 alpha 都有u 正交于 alpha *v 。
- 如果 u 和 v 都正交于 w ,则 u + v 也正交于 w 。
由这两个性质可以得到一个引理:如果u 正交于v ,则对于任意的标量,均有
进一步,对于向量 v_1, v_2 , ... , v_n , 如果对任意一对不相等的 i ,j ,均有v_i正交于v_j ,则称它们是相互正交的。
由此得到对上述引理的一般化描述:
将上述概念应用于消防问题上,可以得到消防车引理(Fire Engine Lemma):
- b 是一个向量
- a 是一个非零向量,则集合 {alpha *a :alpha 属于实数集} 表示一条线 L
- p 是 L 上面的一个点且满足 b - p 正交于 a
受上面引理启发,定义两个重要的向量:
根据上面定义,可以求得
当 a 不等于 0 时
当 a = 0 时
由此可以得到求解 b 的两个分量

def project_along(b, a):
sigma = (b*a)/(a*a) if a*a > 1e-20 else 0
return sigma * adef project_orthogonal1(b, a):
return b - project_along(b, a)消防车问题可以被重新声明为寻找线上的一个向量使其与 b 最近似。
这里的最近似,是最接近的意思。
最接近的概念在很多应用场合会被一再提及,如:
- 最小二乘法,一种基础的数据分析技术
- 图像压缩
- 主元素分析,另外一种数据分析技术
- 潜在语义分析,一种数据检索技术
综上,消防车问题可以描述为:
对这一问题的一种很自然的推广为:
我们将在下周课程中对这种推广进行介绍。








 本博客详细介绍了线性代数中的核心概念,包括高斯消元法及其应用,内积定义与正交原理。深入探讨了求解线性方程的方法,矩阵的零空间,以及如何通过高斯消元法找到矩阵的行空间基底。同时,阐述了内积和正交性的基本理论,并提供了计算向量模、内积和正交向量的方法。
本博客详细介绍了线性代数中的核心概念,包括高斯消元法及其应用,内积定义与正交原理。深入探讨了求解线性方程的方法,矩阵的零空间,以及如何通过高斯消元法找到矩阵的行空间基底。同时,阐述了内积和正交性的基本理论,并提供了计算向量模、内积和正交向量的方法。






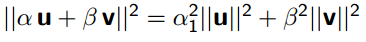



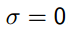
















 3276
3276

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








