本周课程介绍了矩阵(Matrix),主要有以下几点内容:
- 矩阵向量相乘:
- 向量矩阵相乘;
- 矩阵函数关系;
- 矩阵矩阵相乘;
- 矩阵的逆;
- 应用:Hamming Code。
首先,什么是矩阵?传统定义矩阵为一个二维数组。关于矩阵的一些最基础的操作这里不展开来讲。
对于矩阵与向量的乘法运算,可以分为两种:矩阵向量相乘和向量矩阵相乘,而每一种又有两种定义:线性组合(Linear-Combination)和点乘(Dot-Product)。当然要进行合法运算,还需要两者的维数匹配。以下是线性组合定义:
以下是矩阵向量相乘的点乘定义,向量矩阵相乘的点乘定义与此类似:
在矩阵中还有一个比较重要的概念,零空间(Null Space),矩阵M的零空间定义为{u:M *u =0},用Null M表示。
零空间具有三个性质:
- 包含零向量;
- 如果u属于Null M,则有 a * u 也属于Null M(这里a表示一个标量);
- 如果u、v均属于Null M,则有u +v也属于Null M;
另外一个定理:如果u1 是 M *x =b 的一个解,则解集为u1+ V ,其中有 V = Null M。
故有,如果V是平凡向量空间(Trivial Vector Space),则u1是唯一解;如果V不是平凡向量空间,则u1不是唯一解。
进一步,我们可以得到一个推论:当且仅当Null M是平凡向量空间时,M * x =b 最多只有一个解。这里引出一个问题,如何知道一个零空间是否为平凡的(Trivial)。
接下来,探讨矩阵M与函数 f(x) = M *x 之间的关系。
通过函数的定义域(domain)和值域(co-domain),可以轻松得到矩阵的维数,通过给函数赋值基向量,可以得到矩阵M各列的数值,进而得到矩阵M。由此可以引申得到单位矩阵和对角线矩阵的定义。
上面提到的函数 f(x) 是由矩阵与向量相乘得到的,那么怎么样的函数可以用这样的形式表示呢?
先介绍两个重要的代数性质,这两个性质具有如下特点:
- 如果一个函数可以用矩阵向量相乘表示,则它具有这两个性质;
- 如果一个从域F-C(这里F表示域名,C表示维数)映射到域F-R的函数满足这两个性质,那么它可以用矩阵向量相乘表示。
- f(a*v) = a * f(v);
- f(u + v) = f(u) + f(v)。
那么称函数 f 为线性函数(Linear Function)。
根据这个定义,可以得到如下定理:
令 M 为 R*C 矩阵,并令函数 f:F-C -> F-R 定义为 f(x) = M *x ,那么 f 是线性函数。
根据线性函数的两个性质,我们还可以得到另一个定理:
对于线性函数 f ,对 f 定义域上的任何向量v1,v2,...,vn,以及任何标量a1,a2,...,an,有
f(a1v1 + a2v2 + ... + anvn) = a1 * f(v1) + a2 * f(v2) + ... + an * f(vn)。
对于线性函数,有一个重要的概念,核(Kernel):线性函数的核为{v: f(v) =0}。
根据前面的定义,不难看出,对于函数 f(x) = M * x 而言,有 Kernel f = Null M。
由于核与零空间的这种关系,我们可以得到关于核的一些结论。
一对一引理(one to one lemma):一个线性函数是一对一的当且仅当它的核是平凡向量空间。
这里我们引入一个前面章节介绍的概念——映射(Image),对函数 f:V -> W 而言,f 的映射是定义域上所有元素的映射的集合 {f(v):v 属于 V},表示为 Im f,根据这一定义,不难看出,线性函数的映射是一个向量空间。
在这里,我们可以得到两个相同的问题:函数是否为映射的(Onto),和 Im f 是否等于 f 的值域。这个问题可以用于解答灭灯游戏中是否所有配置都是可解的的问题。
对于矩阵矩阵相乘的问题,有如下三种定义方法:
由此引申出内积(Inner Product)和外积(outer Product)的概念。
研究矩阵矩阵乘法与函数合成的关系,可以得到如下定理:
若矩阵A,B满足函数:f(y) = A *y,g(x) = B *x,h(x) = AB *x,则有 f(g(x)) = h(x)。
由此可以得到推论:(AB)C = A(BC)。
沿用上面的定理,我们可以得到矩阵的逆(Inverse)的定义:
若矩阵A,B满足函数:f(y) = A * y,g(x) = B * x,h(x) = AB * x,且 f, g彼此互为逆函数,则 A,B 互为逆矩阵。
当 A,B 互为逆矩阵时,我们说矩阵 A,B 是可逆矩阵(Invertible Matrix)。用 A ^(-1)表示 A 的逆矩阵。
关于为什么要研究逆矩阵,主要有以下三个原因:
- 矩阵向量方程的解的存在性和唯一性:如果矩阵 M 是可逆的,则对于右边的每一个向量 b,方程 M *x =b 有唯一解;
- 如果假设 A 是可逆的,则求解方程 M * x = b 的算法变得非常简单;
- 可逆矩阵在基底变换(Change of basis)中扮演着关键角色。
关于逆矩阵,有如下定理:
对于定义好的矩阵乘积 AB,当且仅当 A 和 B 均为可逆矩阵时,AB 是可逆矩阵。
当且仅当 AB 和 BA 均是单位矩阵时,A 和 B 互为逆矩阵。
如何判定一个矩阵是否是可逆矩阵,这里给出部分解答:
通过定义可知,要使 M 为可逆矩阵,只需要函数 f(x) = M * x 是可逆函数,也就是说函数是一对一的且是映射的。
- 一对一:因为函数的线性的,有一对一引理可以知道,当函数的核是平凡的,也就是说矩阵 M 的零空间是平凡的时候,函数是一对一的;
- 映射的:我们尚未知道如何判定一个函数是否为映射的。如果我们知道如何判定一个线性函数是映射的,那么我们就知道如何判定一个矩阵是否是可逆的。
本周应用内容是错误修正代码(Error Correcting Code):Hamming Code。
下面简要介绍一下Hamming Code的工作原理:
Hamming Code 可以用来修正通讯过程中由于噪声影响造成的数据传输错误。
通讯过程的编码解码过程如图所示。
在通讯过程中,在发送端先将需要发送的半字节数据编码为七位数据再进行传送,在接收端对接收到的七位数据进行解码得到所要的半字节有效数据。在数据传输过程中,由于信道上的噪声干扰,会使接收端接收到的数据与发送端发送数据出现不吻合的现象,所以有必要检查数据传送过程中是否存在错误,并进行必要的修正。
这里,我们用向量 p 表示要传送的半字节数据,用向量 c 表示经过编码得到的数据,用向量 ce 表示接受到的数据,用向量 e 表示传送过程中的引入的错误模型,用矩阵 G 表示编码矩阵,用矩阵 R 表示解码矩阵。运算均基于 GF2 域进行。
则不难得到下面的关系:c = G * p,ce = c + e,p = R * c。
由第一、第三道式子,可以知道 R * G 为单位矩阵。
为了从 ce 中重新提取出 c,只需要从 ce 中提取出 e,这时,有 c = ce + e。
那么如何从 ce 中 提取出 e 呢?
Hamming Code 引入了提取矩阵 H,令 c 属于 C,如果有 C = Null H,则必有 H * c = 0,此时有
H * ce = H * (c + e) = H * c + H * e = 0 + H * e = H * e。
这样问题转换为如何通过 H * e 求得 e。
下面需要对噪声信号进行一些假设:噪声信道最多产生一位错误,即 e 中最多有一个元素是 1。
用 Python 代码表示矩阵 H 为
H = listlist2mat([[0,0,0,one,one,one,one],[0,one,one,0,0,one,one],[one,0,one,0,one,0,one]])这是对每一个 e 都可以求得相应的 H * e,通过查看其中的规律,就可以得到从 H * e 求 e 的求解方法。
一旦可以求得 e,那么我们就可以进行正确的解码了。
这里需要强调一下,Hamming Code 是不支持发现一位以上错误代码的。
对应的矩阵 G 和 R 分别为
G = listlist2mat([[one, 0, one, one],[one, one, 0, one], [0, 0, 0, one], [one, one, one, 0], [0, 0, one, 0], [0, one, 0, 0],[one, 0, 0, 0]])
R = listlist2mat([[0,0,0,0,0,0,one],[0,0,0,0,0,one,0],[0,0,0,0,one,0,0],[0,0,one,0,0,0,0]])
最后将上面整个过程用 Python 总结出来如下,如果你的代码没有错,那么最后 # Test 输出的结果应该是 True:
# Encode
c = G * p
# Add Error
ce = c + e
# Error Correct
cc = ce + Find_error(H * ce)
# Decode
pp = R * cc
# Test
pp == p








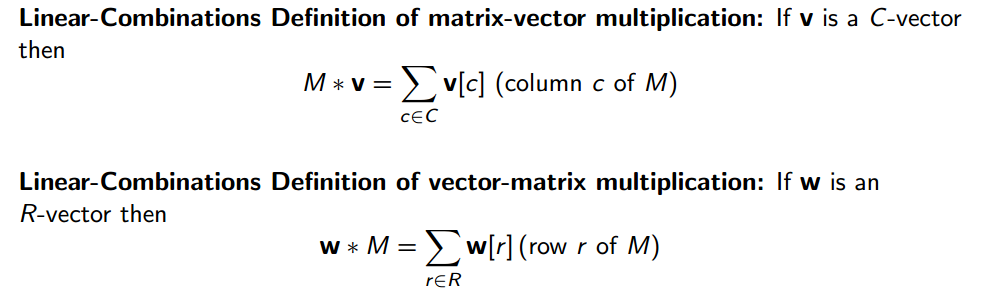


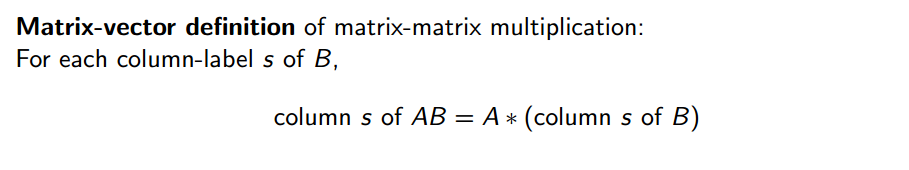
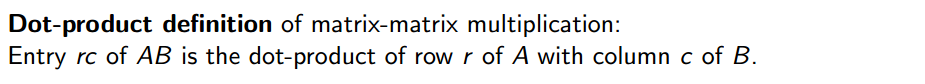















 4104
4104

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








