扫描线3——矩形面积并

原创已于 2025-10-21 15:27:37 修改 · 912 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #数据结构 #算法

于 2025-10-16 20:42:02 首次发布

数据结构专栏收录该内容

12 篇文章

订阅专栏

扫描线

区间信息的查询可以通过离线后用线段树/树状数组进行处理。

求覆盖矩形面积

例题1

在二维平面坐标系中，每次给定四个整数 $x_1,y_1,x_2,y_2$ ，表示矩形的左下角和右上角的位置。

请求出所有被矩形覆盖的区域的面积之和。

题解

若干个矩形覆盖后的图形必然是不规则的，但至少其每条边都平行于坐标轴，这也是为数不多的优点了。

如何求这样的图形的面积呢？

一个好的思路是将图形划分为若干个矩形，对每个矩形面积求和。

那么问题就变成，如何找到一种好的方法使得我们将这样的图形能够划分为若干矩形？

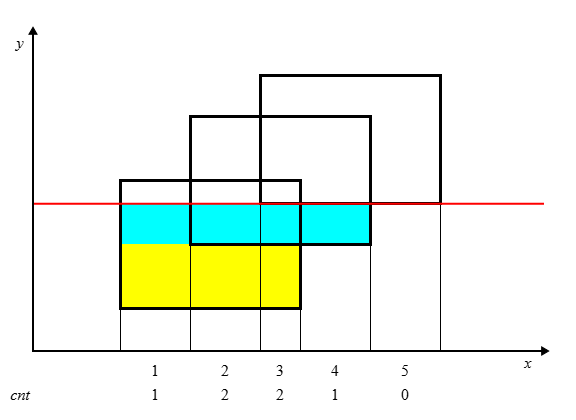
在这里插入图片描述

借助 oiwiki 上的图，这是三个矩形叠加的图形，我们用一根横线从底到高开始扫描。

当横线到达 $y_1$ 的时候，这是图形的最低处，显然 $y=y_1$ 时的在 $x$ 轴上的横向长度 $len_1$ 可以作为一个矩形的底边。

当横线遇到了 $y_2$ ，也就是倒数第二低的位置时，说明此时我们可以进行一次结算，必然能在原图中找到以 $len_1$ 为底，以 $y_2-y_1$ 为高的矩形，这是我们第一次划分出一个矩形。紧接着我们可以发现 $y=y_2$ 这条边是某个矩形的底，所以我们将 $y=y_2$ 时图形在 $x$ 轴上的横向长度 $len_2$ 累加到我们的长度里。

如果 $len_1$ 和 $len_2$ 具有重叠部分，那么这个重叠部分只算一次，我们需要的只是在 $x$ 轴上的累加长度。

接着横线到达 $y_3$ ，这是倒数第三低的位置，继续进行一次结算，我们必然能够在图中划分出一个长度为当前在 $x$ 轴上累加的长度 $l e n$ ，宽度是 $y_3-y_2$ 的矩形，并且我们发现 $y=y_3$ 是一个矩形的底部，所以我们将图形在 $y=y_3$ 时的 $x$ 轴上的长度累加到我们当前的长度内。

我们的 $x$ 轴上的长度目前累加了三条矩形的底边，但是我们计算的总长度应该是它们的并。

接下来，我们划分矩形累加面积的同时，需要关注的是当我们遇到了一个矩形的顶端，那么我们需要删去在我们已经累积长度中的对应矩形的底端，这是因为此后这个矩形不会再产生贡献了。

具体流程

我们先将所有的矩形信息离线为如 $x,y_1,y_2,flag)$ 的形式。

$x,y_1,y_2,flag)$ 蕴含的是一个矩形的 左或右边界 信息。其中 $x$ 表示边界在 $x$ 轴的位置， $y_1,y_2$ 是这个边界的上界与下界， $f l a g = 1$ 说明是当前信息是左边界，如果 $f l a g = 0$ 说明是右边界。

将所有信息按 $x$ 从小到大排序，假设我们现在需要维护一个从左到右的扫描线。

扫描线维护的就是当前已扫过的边界信息在 $y$ 轴上的 覆盖长度。

有了覆盖长度我们就可以不断地将图形划分为一个高度是覆盖长度，宽度是 $x_i-x_{i-1}$ 的矩形。

现在问题是，我们如何维护在 $y$ 轴上的覆盖长度：

如果 $f l a g$ 是 $1$ ，说明新遇到了一个矩形，即要在 $y$ 轴上进行覆盖。
如果 $f l a g$ 是 $0$ ，说明已经离开了一个矩形，即要撤销其在 $y$ 轴上的覆盖。

由于所涉及的区间可能过大，我们不可能真实地模拟区间覆盖，这时就需要进行 离散化。

我们将所有涉及到的端点离散出来后，问题就变成我们该怎么计算覆盖长度？

假设有 $k$ 个不同的 $y$ 端点，将 $y$ 端点进行排序后，我们令线段树里的第 $i$ 个结点表示的区间是 $yi∼yi+1y_i\sim y_{i+1}$ 。

因为我们需要支持区间的覆盖与撤销覆盖，并且一个区间不管覆盖多少次，我们都只计算其有效长度。

所以至少需要维护 区间有效长度 和 区间覆盖次数 两种信息。

我们要覆盖 $y_{i},y_{j}]$ 的真实区间，那么就相当于 覆盖一次 离散化后的区间 $pos[y_{i}], pos[y_{j}]-1]$ 。

考虑如何合并信息

父亲的区间有效长度应是其左右儿子的区间有效长度之和。

父亲的区间覆盖次数应是左右儿子的区间覆盖次数取 $min⁡\min$ 。

注意会出现 儿子被覆盖但是父亲没有被覆盖 的情况，因为我们的覆盖指的是完整地覆盖当前结点所表示的区间。

所以，如果 当前结点 覆盖次数为 $0$ ，不意味着当前结点的区间有效长度是 $0$ 。

但若 当前结点 覆盖次数不为 $0$ ，那么当前结点的区间有效长度应该是 其维护的区间的总长度。

所以我们考虑再维护一种信息 区间总长度。

考虑如何更新信息

我们要覆盖离散化区间 $pos[y_{i}],pos[y_{j}]-1]$ ，即递归地覆盖 $pos[y_i],pos[y_j]-1]$ 在线段树中的极大子集。

说人话就是假设当前结点维护的区间是 $[L, R]$ ，当我们发现 $pos[yi]≤L≤R≤pos[yj]−1pos[y_i]\le L\le R\le pos[y_j]-1$ 时，这个结点就是所寻区间的一个极大子集，为什么极大呢？因为这个结点的子树中所有结点都是所寻区间的子集，而它比子树内的所有结点都大，所以我们只需要操作它就行了，不需要访问到子树内。

我们在上文中写道， $n o d e$ 的覆盖次数等于左儿子的覆盖次数与右儿子的覆盖次数的 $min⁡\min$ 。

现在看来是不准确的，因为如果一个操作先给 $n o d e$ 的覆盖次数加 $1$ 后，再给其左儿子覆盖次数加 $1$ 。

但如果遵循上述的合并规则， $n o d e$ 的覆盖次数只有 $0$ 次了。

所以我们应该分开维护，用 $co v er S o n$ 表示儿子传来的覆盖次数， $co v er S e l f$ 表示直接操作自身的覆盖次数。

因为我们添加了一条矩形边时，后续一定会存在一次删除对应边。

在删除对应边操作时，我们就直接减去极大子集处的 $co v er S e l f$ ，因为当初加的就是 $co v er S e l f$ 。

我们还有了一个惊人的发现就是，因为 $co v er S e l f$ 不需要往下传，而 $co v er S o n$ 的来源实际上是子孙结点的 $co v er S e l f$ ，这意味着我们不需要进行懒标记更新，只需要向上传递更新就行了。

考虑如何查询信息

这道题里我们查询的是 $y$ 轴被覆盖区间的总长度，所以就是根结点。

#include <bits/stdc++.h>
using namespace std;
//#pragma GCC optimize(2)
#define int long long
#define endl '\n'
#define PII pair<int,int>
#define INF 1e18

struct SegmentTreeNode {

    // 矩阵面积并
    int lenActual;
    int len;

    int coverSon;
    int coverSelf;


    SegmentTreeNode() {
        len = 0;
        lenActual = 0;

        coverSon = 0;
        coverSelf = 0;
    }
};

struct SegmentTree {

    // 树信息
    int n;
    vector <int> a; // 原始序列信息
    vector <SegmentTreeNode> tr;

    SegmentTree(int _n) {
        n = _n;
        a.assign(n + 1, 0);
        tr.assign(n << 2, SegmentTreeNode());
    }

    SegmentTreeNode merge(SegmentTreeNode a, SegmentTreeNode b) {
        SegmentTreeNode fa;
        fa.lenActual = a.lenActual + b.lenActual;
        fa.coverSon = min(a.coverSon + a.coverSelf, b.coverSon + b.coverSelf);
        return fa;
    }

    void pushup (int node) {
        SegmentTreeNode now = merge(tr[node << 1], tr[node << 1 | 1]);
        tr[node].lenActual = now.lenActual;
        tr[node].coverSon = now.coverSon;

        int allCover = tr[node].coverSelf + tr[node].coverSon;
        if (allCover > 0) tr[node].len = tr[node].lenActual;
        else tr[node].len = tr[node << 1].len + tr[node << 1|1].len;
    }

    SegmentTreeNode query (int node, int L, int R, int l, int r) {
        if (R < l || L > r || l > r) return SegmentTreeNode();

        if (l <= L && r >= R) {
            return tr[node];
        }

        int mid = L + R >> 1;
        SegmentTreeNode q1 = query (node << 1, L, mid, l, r);
        SegmentTreeNode q2 = query (node << 1 | 1, mid + 1, R, l, r);

        return merge(q1, q2); // 返回合并起来的信息，不一定是求和
    }

    void add(int node, int L, int R, int l, int r, int val) {
            if (l > r || l > R || r < L) return;

            if (l <= L && r >= R) {
                tr[node].coverSelf += val;

                int allCover = tr[node].coverSelf + tr[node].coverSon;
                if (allCover == 0) {
                    if (L == R) tr[node].len = 0;
                    else tr[node].len = tr[node << 1].len + tr[node << 1|1].len;
                } else {
                    tr[node].len = tr[node].lenActual;
                }
                return;
            }

            int mid = (L + R) >> 1;
            add(node << 1, L, mid, l, r, val);
            add(node << 1|1, mid + 1, R, l, r, val);

            pushup(node);
            return;
    }

    void change(int node, int L, int R, int pos, int val) {
           if (pos < L || pos > R) return;

           if (L == R && L == pos) {
                tr[node].lenActual = val;
                return;
           }

           int mid = L + R >> 1;
           change(node << 1, L, mid, pos, val);
           change(node << 1|1, mid + 1, R, pos, val);

           pushup(node);
           return;
    }
};

struct Query {
    int x;
    int y1;
    int y2;
    int flag;
};

void slove () {
    int n;
    cin >> n;

    map <int, int> mpy;
    vector <Query> queries;
    for (int i = 1; i <= n; i++) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;

        mpy[y1] = 1, mpy[y2] = 1;

        queries.push_back(Query{x1, y1, y2, 1});
        queries.push_back(Query{x2, y1, y2, 0});
    }

    sort (queries.begin(), queries.end(), [](Query A, Query B) {
         return A.x < B.x;
    });

    int cnt = 0;
    for (auto &i : mpy) {
        i.second = ++cnt;
    }

    vector <int> posy (1);
    for (auto i : mpy) {
        posy.push_back(i.first);
    }


    SegmentTree tt(cnt);
    for (int i = 1; i <= cnt - 1; i++) {
        tt.change(1, 1, cnt - 1, i, posy[i + 1] - posy[i]);
    }

    int ans = 0;
    for (int i = 0; i < queries.size(); i++) {
        int len1 = queries[i].x;
        if (i != 0) len1 -= queries[i - 1].x;
        int len2 = tt.tr[1].len;

        ans += len1 * len2;
        if (queries[i].flag == 1) {
            tt.add(1, 1, cnt - 1, mpy[queries[i].y1], mpy[queries[i].y2] - 1, 1);
        } else {
            tt.add(1, 1, cnt - 1, mpy[queries[i].y1], mpy[queries[i].y2] - 1, -1);
        }
    }
    cout << ans << endl;
}

signed main () {
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    slove();
}