Opencascade官方教程之拓扑篇（Topology）

宁波莱布尼茨信息技术有限公司

已于 2025-04-16 15:02:44 修改

阅读量3.4k

点赞数 29

分类专栏：《opencascade从入门到进阶》文章标签： c++

于 2024-10-22 13:56:03 首次发布

本文链接：https://blog.csdn.net/loujiand/article/details/143111627

版权

《opencascade从入门到进阶》专栏收录该内容

7 篇文章

订阅专栏

在这里插入图片描述

一、拓扑的目的

一般来说，拓扑是描述对象局限性的一种手段，在opencascade中拓扑被称为shapes(形状)。
Opencascad的拓扑是用来描述如下几方面：

物体的边界。
对象之间的连接（通过公共边界）。

二、拓扑的定义

拓扑形状是根据这两个概念定义的：

抽象拓扑（TopoDS）：通过描述有界和有界对象之间的关系来定义数据结构。
Example: 边由其边界（即顶点）描述。
边界表示（B-Rep）：通过关联拓扑和几何信息来完成对象的定义。
Exanple: 一条边位于曲线上并由点界定。

摘要：边界表示和算法类被分组在不同的包中。

抽象类：

抽象拓扑数据结构 （TopoDS），拓扑的几何边界表示 (BReP)

算法类：

直接构造：BRepBuilderAPI , BRepPrimAPi, BRepOfTsetAPI,BRepFilletAPI
布尔操作：BRepAIgOAPI
集合工具：BRepTools
图形数据结构的遍历：TopExp
高级建模功能：BRepFeat

三、为什么要进行边界表示？

B-Rep 有多种替代方案：

构造立体几何（CSG)不允许对任意数字进行建模。
二维图纸不适合下游工程操作。
多个固体可能对应于一个线框模型。
网格不支持弯曲几何体。

B-Rep它是玻璃性的、冗长的、复杂的，这是他的缺点。B-Rep模型使用顶点、边和面作为几何载体，但也有特殊的拓扑类型。模式复杂性导致脆弱性。

四、拓扑形状

定义了以下类型的拓扑形状：

Vertex(端点): 一个点。
Edge(边缘):一部分受顶点限制的曲线。
Wire（边界线）: 一组边（通过它们的顶点连接）。
Face(面):一部分由边界线限制的表面。
Shell(壳体):一组面（通过它们的边连接）。
Solid(实体): 一部分受壳体限制的实体。
.Compsolid(复合实体):由面连接的一组实体。
Compound(复合体): 由任意拓扑形状组合的群体。
-

五、几何结构

下图显示了复杂形状（图中的实体）的子形状之间关系的示例案件）：

在这里插入图片描述

六、shapes间的关系

如果两个形状共享一些边界子形状，则它们是连接的.

Example：让我们考虑两条边 - e1 和 e2。它们中的每一个都受到其边界的限制，边界是顶点（e1 为 v1 f 和 v1 l，e2 为 v2f 和 v2l）。当这两条边共享一个公共顶点 v3 时，它们是已连接的。

在这里插入图片描述

七、shapes间的层次结构

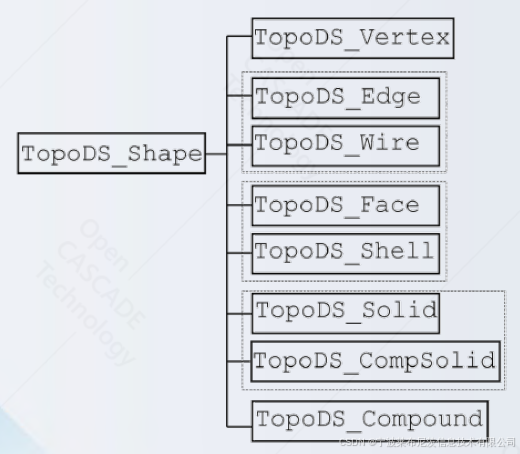
TopoDS_Shape 是所有拓扑形状类的基类。

TopoDS_Vertex 保存有关点（零维对象）的信息。
TopoDS_Edge 保存有关曲线（一维对象）的信息。
TopoDS_Wire 是边的集合。
TopoDS_Face 保存有关表面（二维对象）的信息。
TopoDS_Shell 是面的集合。
TopoDS_Solid、TopoDS_Compsolid 保留有关实体的信息。
TopoDS_Compound 表示一个形状，它是形状的集合。

七、shape的结构

TopoDS_Shape 类被以下信息定义形状：

一个TopoDS_TShape句柄（TopoDS包）
局部坐标系（TopLoc 包）
一个原点 (TopAbs 包)

TopoDS TShape：一个句柄类，用于描述默认坐标系中的对象。这个类从来不会直接使用，而是使用TopoDS_Shape。

TopLoc_Location：定义了局部坐标系所在的位置。与定义位置不同的形状。

在这里插入图片描述

Example：所有这些Boxes共享相同的 TShape，但具有不同的位置。

在这里插入图片描述

TopAbs_orientation：描述形状如何根据材料（或内部和外部区域）界定几何形状。

在这里插入图片描述

当在该形状的上下文中考虑时，形状的方向和位置参数也被假定影响其子形状。当一个形状探索为子形状时，子形状的方向和位置将与主形状的方向和位置相结合。这确保了子形状的参数在引用它的每个形状的上下文中的一致解释。例如，当在这些面的上下文中探索时，两个连接的面共享的边将具有相反的方向。

八、shape的操作

TopoDS_Shape 类及其子类提供了各种有用的方法，例如：

访问TShape：

IsNull() 检查TShape是否为空.
Nullify() - 使 TShape 智能指针为空。

访问Location

Location() - 返回现有位置。
Move() - 将变换应用到实际shape
Moved() - 返回应用变换的新的shape

ShapeType() - 返回 TopoDS_Shape 的类型

shapes比较

IsPartner()——相同的TShape
IsSame()——相同的 TShape 和位置
IsEqual()——相同的 TShape、位置和方向
-

九、shape向下转换

TopoDS_Shape 对象通过值进行操作。这就是为什么要实现特殊方法来提供向下转换功能：

TopoDS::Vertex() 返回一个TopoDS_Vertex
TopoDS::Edge() 返回一个 TopoDS_Edge
TopoDS::Wire() 返回一个 TopoDS_Wire
TopoDS::Face() 返回一个 TopoDS_Face
TopoDS::Shell() 返回一个 TopoDS_Shell
TopoDS::Solid() 返回一个 TopoDS_Solid
TopoDS::CompSolid() 返回一个 TopoDS_CompSolid
TopoDS::Compound() 返回一个 TopoDS_Compound
注意：当转换不当时会引发异常。

Example：第一个块是正确的，但第二个块被编译器拒绝。

//正确
if(aShape.ShapeType()== TopAbS_VERTEX)
const TopoDS_Vertex& aVl =TopoDS::Vertex(aShape);
//被编译器拒绝
if(aShape.ShapeType()== TopAbS_VERTEX)
TopoDS_Vertex aV2 = aShape;

十、shape的集合

TopTools 包提供一下功能：

用于计算具有或不具有方向的shape的哈希码(hash)的类。
shape集合的实例化。

BRep_Builder BB;
TopTools_MapOfShape anEmap = anItl.Value();
TopTools_ListIteratorOfistOfShape anItl(anEdges);
for (;anItl.More();anItl.Next()) 
	BB.Remove(aWire,anItl.Value());
for (anItl.Initialize(edges);anItl.More();anItl.Next())
{
	TopoDS_Shape anEdge =anItl.Value();
	if (anEmap.Contains(anEdge))
		anEdge.Reverse();
	BB.Add(awire,anEdge);
}

十一、遍历工具

遍历拓扑形状意味着找到它的子形状，可能符合特定的标准。

TopoDS_Iterator 类遍历给定形状的第一级子形状（从其列表中的TShape）。
TopExp_Explorer 类探索给定形状中的所有子形状，并可以选择实体类型（例如，仅限face）。

TopExp_Explorer anExp(aShape，TopAbs_EDGE);
for (;anExp.More();anExp.Next())
{
TopoDS_Edge anEdge = TopoDs::Edge(anExp.Current());
}

TopExp::MapShapes() 方法遍历子形状并将它们放入map中（从而检测相同的元素）
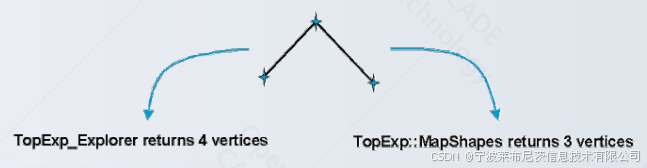
TopExp: :MapShapesAndAncestors() 方法返回引用另一个实体的所有实体。

在opencascade中，没有从子形状到其父类形状的反向指针。相反，可以使用 TopExp::MapShapesAndAncestors() 来恢复此信息。例如，如果您想查找包含给定顶点或边的所有面，您可以使用此方法。

十二、边界表示

边界表示（B-Rep）以三个维度描述模型对象。在 B-Rep 建模中，实体由其边界表示。

在这里插入图片描述

B-Rep 将几何融入拓扑：

几何：面位于曲面上，边位于曲线上，顶点位于点上
拓扑：形状的连通性。

这样描述一个模型对象就完整了

B-Rep描述基于：

TopoDS 描述对象的拓扑结构。
Geom 和 Geom2d - 描述这些对象的几何形状。

十三、B-rep实体

定义 BRep_TVertex、BRep_TEdge 和 BRep_TFace 是为了向拓扑模型添加几何信息。

BRep_TVertex、BRep_TEdge 和 BRep_TFace 继承于 TopoDS_TShape。

根据拓扑实体的不同，几何信息的存储方式也不同。存储允许描述的几何信息的实体。

边：受顶点限制的曲线。
面：由边缘限制的表面。
实体：受面限制的空间。

十四、BRep _Vertex 中的几何

3D 点 (gp_Pnt) - 对于所有顶点

点表示的列表可以是如下内容:

曲线上的点（Geom_Curve，参数）如果顶点界定边。
曲面上曲线上的点（Geom_Surface、Geom2d_Curve、参数）如果顶点界定位于曲面上的边。
曲面上的点（Geom_Surface、Uparameter、Vparameter）如果顶点边界面上。
-

十五、BRep _Edge 中的几何

BRep_TEdge 几何图形存储为曲线表示列表，可以是：

一条 3D 曲线和曲线上的两个参数（Geom_Curve、FirstParameter、LastParameter）。
曲面上的一条曲线、曲线上的两个参数和曲面上的两对参数 (Geom2d_Curve.第一个参数、最后一个参数、Geom_Surface、FirstUVCoord、LastUVCoord）。

SameParameter 属性指示边缘的不同表示是否同步参数化，即 3D 曲线上具有相同参数值的点与每条 2D 曲线重合（在边缘的公差内）

在这里插入图片描述

十六、BRep_TFace 中的几何

BRep_TFace 几何图形存储为 Geom_Surface

在这里插入图片描述

十七、B-Rep 的精确度

多个几何表示可以附加到拓扑（B-Rep）对象。例如，一个 vertex可以表示为：

3D点；
曲线上的参数；
表面上的一对参数。

这些表示类似，但很少相同。对于建模算法，有必要确切地知道与该近似值相关的精度。该精度的数值与每个 B-Rep 形状相关联，称为公差。它定义了对象的代数表示所在的区域。

在 BRep_TVertex 精度定义了 3D 点周围的球体半径：

在这里插入图片描述

在 BRep_TEdge 中，精度定义了 3D 曲线周围管道的半径

在这里插入图片描述

在 BRep_TFace 精度中定义了表面上方和下方的厚度

在这里插入图片描述

由于公差与几何载体相关，因此它是由创建的算法定义的或修改 B-Rep 中的几何形状。

Opencascade技术要求：公差(顶点)>=公差(边)>=公差(面)

在这里插入图片描述

十八、BRepAdaptor（适配器包）

OCCT 可以通过适配器模式在几何算法中使用拓扑实体。边界表示适配器用作修剪曲线和曲面，从而消除了手动修剪的必要性。可以使用以下适配器：

BRepAdapter_Curve-曲线适配器接受边
BRepAdapter_Curve2d - 接受边和面的曲线适配器。
BRepAdapter_CompCurve-接受wire的曲线适配器。
BRepAdaptor_Surface-表面适配器接受面。

注意：可提供Handle版本的适配器。例如，BRepAdaptor_HSurface 类是表面适配器的处理版本。

十九、B-Rep 的特殊性

3D 空间（3D 拓扑）和参数空间（UV 拓扑）中同一面的表示通常拓扑相似。

在这里插入图片描述

有时 3D 拓扑和 UV 拓扑是不同的。这是接缝边缘和退化边缘的情况。

接缝边是定义封闭面上（通常构建在周期曲面上）上的接缝的边。在这种情况下，一个 3D 拓扑对应于多个 UV 拓扑。
当一条或多条 UV 2d 曲线对应于单个 3D 顶点时，edae 被称为退化。此类边没有 3d 曲线表示，并且包含相同的顶点两次（具有相反的方向）。

二十、shapes的构造

Open CASCADE Technology 提供了多个软件包，为建模算法提供高级 API，这个 AP 既简单又强大：

简单，因为只需要调用一次函数即可创建对象

gp_Pnt aP1(10.0，0.0，0.0)，aP2(20.0，0.0，0.0);
TopoDS_Egde E=BRepBuilderAPI MakeEdge(aPl,aP2);

功能强大，因为它包括错误处理和对算法提供的额外信息的访问

gp_Pnt aP1(10.0，0.0，0.0)，aP2(20.0，0.0，0.0);
BRepBuilderAPI_MakeEdge aME(aP1,aP2);
//Construction state.
if (!aME.IsDone())
{
std::cout << "Error. MakeEdge failed:"<< aME.Error()<< std::endl;
}
//Edge extraction from algorithm.TopoDS Edge anEdge= aME.Edge();

二十一、BRepBuilderAPl（建模包）

该包包含以下类：

1.从几何实体直接构造拓扑对象或组合拓扑物品形状类似于collection:

BRepBuilderAPI_MakeVertex: 从点构建顶点。
BRepBuilderAPI MakeEdge/BRepBuilderAPI MakeEdge2d: 从曲线构建边缘。.
BRepBuilderAPI_MakePolygon: 从点构建一条线。
BRepBuilderAPI_MakeWire: 从边缘构建一条线。
BRepBuilderAPI_MakeFace:从曲面构建面。
BRepBuilderAPI_MakeShell:从表面构建外壳（分割为 C2 块）。
BRepBuilderAPI_MakeSolid: 用壳构建实体。

2.修改对象：

BRepBuilderAPI_Transform: 对形状应用变换。
BRepBuilderAPI_Copy: 进行形状的深度复制。
BRepBuilderAPI_Sewing: 通过合并边界边从一组面构建壳。

二十二、BRepPrimAPI（建模包）

该包包含以下类：

1.创建原始对象：

BRepPrimAPI_MakeBox：生成立方体
BRepPrimAPI_MakeWedge：生成楔体
BRepPrimAPI_MakeSphere：球体
BRepPrimAPI_MakeCone：生成圆台
BRepPrimAPI_MakeCylinder：生成圆柱
BRepPrimAPI_MakeTorus：生成环面
BRepPrimAPI_MakeHalfSpace：生成立方体

2.创建扫描体：

BRepPrimAPI_MakePrism：法相拉伸体
BrepPrimAPI_MakeRevol：旋转生成体

二十三、位置变换

OCCT 中提供的数据共享概念允许通过位置多次重复使用拓扑信息和实例模型。形状内的位置是一组连续的变换，它们被作为单个变换进行操作。

注意：空位置和现有的相同位置被视为不同。结果，IsSame() 检查将返回 false。

位置变换方法如下：

Location
Move
Moved

// Construct location.
gp_Axl axis(gp_Pnt(aX,aY,a2),gp_Vec(aDX，aDY,aDz));
gp_Trsf T;
T.SetRotation(axis,aR);
//Update existing location.aShape.Move(T);

二十四、定向边缘内的顶点

OCCT定向概念旨在通过内部和外部区域的信息完成边界表示。该信息是一组影响形状正确性的规则

方向本身对于顶点没有任何意义。仅当顶点限制某些边时，顶点方向才有意义。边是使用一对顶点构造的（在周期曲线的情况下至少一个顶点使用两次）；按照约定，第一个顶点具有 TOpAbS_FORWARD 方向，第二个顶点具有 TopAbS_REVERSED 方向。

注意：BRepBuilderAPI_MakeVertex 以 TopAbS_FORWARD 方向构造一个 vertex。

gp_Pnt aP1(10.0，0.0，0.0)，aP2(20.0，0.0，0.0);
TopoDS_Edge anEdge = BRepBuilderAPI_MakeEdge(aPl,aP2);
TopExp_Explorer anExpEV(anEdge,TopAbs_VERTEX);
for(;anExpEV.More();anExpEV.Next())
{
	const TopoDS_Vertex& aV=TopoDS::Vertex(anExpEV.Current());
	const gp_Pnt& aPnt=BRep Tool::Pnt(aV);
	if (aV.orientation()== TopAbS FORWARD)
	{
		std::cout<<"Forward vertex is :"
			<<aPnt.X()<<"  "
			<<aPnt.Y()<<"  "
			<<aPnt.Z()<<std::endl()
	}

else if(aV.orientation()== TopAbS REVERSED)
// There is inner orientation. That is why
//else-if expression is needed.
{
			std::cout<<"Reversed vertex is :"
			<<aPnt.X()<<"  "
			<<aPnt.Y()<<"  "
			<<aPnt.Z()<<std::endl()
}