Opencascade官方教程之几何篇（Geometry）

宁波莱布尼茨信息技术有限公司

已于 2025-04-16 15:12:47 修改

阅读量2.6k

点赞数 24

分类专栏：《opencascade从入门到进阶》文章标签： c++ 1024程序员节

于 2024-10-23 14:05:51 首次发布

本文链接：https://blog.csdn.net/loujiand/article/details/143180953

版权

《opencascade从入门到进阶》专栏收录该内容

7 篇文章

订阅专栏

在这里插入图片描述

一、 MVC-模型-视图-控制器

Opencascade提供了一组类，用户可以“按原样”应用或通过添加自定义类来扩展。处理某些概念（例如几何实体）的类通常按实现层进行分组：

模型、视图和控制器：

在这里插入图片描述

每层都在相应的包中实现，而包又包含类和函数。

二、 MVC案例

Example:二维圆的概念

Model

包含圆心和半径的数据对象。
标准的直接构造函数：默认构造函数、带有点和半径的构造函数等。

Controller

画一个经过 3 个点的圆。
画一个以圆心且与直线相切的圆
注意：每个控制器类都有一个返回抽象数据对象的方法

View

你在查看器中的对象

三、 MVC的优劣

和所有事物一样，MVC有一些优点和缺点

优点：

模型是经常存在的：可以在不更改模型类的情况下添加新的控制类。
模型是最小的：在程序执行期间需要时创建控制器类的实例。

缺点

有时，很难找到解决特定问题的类。

四、 MVC控制器类的实现

在 Open CASCADE 技术中实现的各种控制器类，用于几何和拓扑对象包括

直接构建（gce_MakeCircle、gce_MakeLin2d）。
通过二维约束构建（GccAna_Circ2d2TanRad）。
复杂的构建算法：插值近似、投影（GeomAPl 包）

五、非参数和参数几何

非参几何

这些类型由值操纵
这些类没有继承

其他信息可以在文档中找到：

基础课程用户指南。
数据建模用户指南。
建模算法用户指南。

有参几何

eom(Geom2d) 中的实体由Handle 操作（对于数据共享很有用），而控制器类则由值操作。
类的层次结构通常遵循 STEP(ISO 10303) 标准。
提供从Geom到gp来回的方法

其他信息可以在文档中找到：

数据建模用户指南。
建模算法用户指南。

六、非参几何

模型类（二维类可通过添加“2d”后缀，gp_Pnt2d）：

gp_Pnt 笛卡尔点。
gp_Vec 向量。
gp_Dir 方向（大小等于 1.0 的非空向量。
gp_Trsf 欧几里得变换。可以独立设置平移、旋转和缩放。
gp_Ax1 轴是点加方向。
gp_Lin、gp_Circ、gp_Elips、gp_Hypr、gp_Parab、gp_Cylinder、gp_Sphere、gp_Torus
（表示曲线和曲面的基元）

控制类

直接构建 gce_MakeCircle、gce_MakeLin
约束构造（仅限 2d）-GccAna_Circ2d2TanRad

七、非参数几何的限制

非参数几何提供了有用的集合类，但它们存在一些原则限制：

无法回答典型的几何问题：

此时的曲率值是多少！
此时曲线的切向量是多少？
曲线和给定点之间的最小欧几里德距离是多少？
这些对象相交吗？

有些对象是无限的，并且没有办法让它们变得有限：

直线、双曲线、抛物线。
平面、圆柱体。

不可能表示自由形式和非平凡的对象：

如何表示平面本身？（贝塞尔曲线和 B 样条曲线）。
如何表示偏置曲面？（需要正常）。
如何表示扫掠曲面？（线性挤压和旋转）。

八、参数几何体

模型类（Geom2d 包中提供了二维类）：

曲线 Geom_Curve 的子类

Geom_Line
Conics：Geom_Circle、Geom_Ellipse、Geom_Hyperbola、Geom_Parabola
自由形式：Geom_BSplineCurve、Geom_BezierCurveGeom_0ffsetCurve
修剪概念：Geom_TrimmedCurve

Geom_Surface 表面子类：

基本曲面：Geom_Plane、Geom_CylindricalSurface、Geom_SphericalSurface Geom 、Geom_ToroidalSurface、Geom_ConicalSurface
自由形式：Geom_BSplineSurface、Geom_BezierSurface
扫掠曲面：Geom_Surface0fLinearExtrusion、Geom_SurfaceOfRevolution
偏置曲面：Geom_OffsetSurface
修剪概念：Geom_RectangularTrimmedSurface

控制器类（二维类可以通过在包名 gce2d 中添加“2d”后缀来获得）：

直接构造 gce_MakeCircle、gce2d_MakeCircle
约束构造（仅限2d Geom2dGcc_Circl2d3Tan

九、修剪概念

一些参数对象，如线 (Geom_Line) 或平面 (Geom_Plane)，是无限的，因为它们的非参数对应项。怎么绑定他们呢？

曲线：使用起始和结束参数 -Geom_TrimmedCurveSurface
使用矩形域进行表面绑定：Geom_RectangularTrimmedSurface

OCCT 无法防止边界外的表面评估。此功能用于高级算法，例如偏移算法，但建议避免在参数域之外进行评估。

在这里插入图片描述

十、二维几何约束

在 Open CASCADE 技术中，2D 中的曲线（或轮廓）具有隐式方向，并且“interioi”的概念区域”被定义。

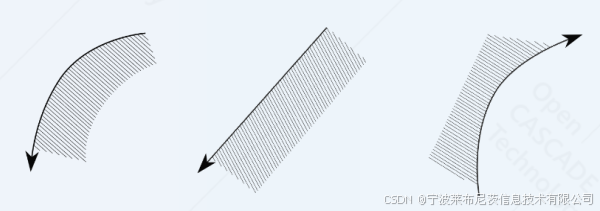
在这里插入图片描述

按照惯例，根据曲线描述的正方向，曲线的内部位于左侧。约束几何创建涉及参数的限定，即参数相对于解决方案的位置：

外部——解决方案和论证彼此外部。
封闭 - 解决方案包含了论点。
附上 - 解决方案包含在论证中。

以C1和C2为参数，确定C1和C2的切线问题有4个解。这些解可以通过外定位和包围定位来实现。封闭定位会导致异常，因为线不能位于圆内。

在这里插入图片描述

用于创建约束几何体的包列表:

GccAna 基本几何的算法案例。
Geom2dGcc 高级几何的算法类。
GccEnt 参数限定的方法和类型。

Example:

#include <GccEnt.hxx>
#include <GccAna_Circ2d2TanRad.hxx>
void ToDo(const gp_Circ2d& aCl, const gp_Circ2d& aC2) 
{
		GccAna_Circ2d2TanRad aSolCirc(GccEnt::Outside(aCl), GccEnt::Enclosing(aC2), aRadius, aTolerance);
if (aSolCirc.IsDone())
	{
		for (Standard_Integer i = 1; i <= aSolCirc.NbSolutions (); i++) 
			{
				gp_Circ2d aCircle = aSolCirc.ThisSolution(i); 
			} 
	}
}

十一、浮点：实现和限制

现代计算机使用lEEE 754作为表示实数的方式（替代方案是对数系统、区间算术、unum / posit），根据标准实值表示为以下形式：

在这里插入图片描述

其中有效数和指数是整数，例子

在这里插入图片描述

下表展示了常见类型的位分布：

在这里插入图片描述

精度的固定位数会导致舍入和表示错误。所以，每个算法都使用浮点点应附有容差值以覆盖这些误差。

十二、几何公差和精度

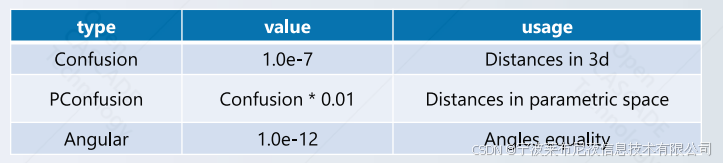
OCCT提供了一套几何公差，旨在克服浮点问题。这些公差位于Precision package:

在这里插入图片描述

Example:

// Returns true when the given point is located in origin. 
static Standard_Boolean IsOrigin(const gp_Pnt& thePnt) 
{
const gp_Pnt& anOrigin = gp::Origin();
if (anOrigin.Distance(thePn ) < Precision::Confusion()) 
return Standard_True;
return Standard False;
}

十三、插值与近似值

插值：插值是找到一个通过所有点的多项式。

它们的典型问题是:

结果中的高阶多项式（取决于插值算法）。
复杂的结果。
振荡是可能的

近似是多项式构造的过程，它接近给定的点集但不完全通过它们。

近似算法有以下缺点：

与插值相比，它的计算量更大。
与插值相比，需要更多的努力来调整参数。

十四、曲线插值

OCCT提供曲线插值算法。可以使用或不使用与点关联的参数来运行它。用法很简单：

// Prepare data to be converted.
Standard_Integer aPos = 1;
Handle(TColgp_HArraylOfPnt) aPnts = new TColgp_HArraylOfPnt(1, 100);
// Fill points 
• • •
// Launch interpolation algorithm.
GeomAPI_Interpolate anlnterpolator (aPnts, Standard_False, Precision::Confusion()); 
anlnterpolator.Perform();
// Check done state.
if (!anlnterpolator.IsDone()) 
{
std: :cout « "Error: interpolation failed. *' « std::endl;
return 0;
}
Handle(Geom BSplineCurve) aCurve = anlnterpolator.Curve();

十五、带切线的曲线插值

插值问题有无穷个解：

在这里插入图片描述

可以使用起点和终点处的切线来选择特定的解决方案：

GeomAPT Interpolate anlnterpolator(aPnts, Standard_False, Precision::Confusion()); 
anlnterpolator.Load(gp_Vec(1.0, 0.0, 0.0),
gp_Vec(0.0z 1.0, 0.0)); // Load tangents.
anlnterpolator.Perform();

十六、曲线近似

OCCT 具有近似内置曲线近似算法。它可以按如下方式使用：

// Construct array to be approximated. 
TColgp_ArraylOfPnt aPnts(l, 100);
// Fill points. 
• • •
GeomAPI_PointsToBSpline anApproximator;
anApproximator.Init(aPnts, 1.0, 0.0, 0.0, 8, GeomAbs_C2, 0.001);
if (!anApproximator.IsDone()) 
{
std::cout « "Error: approximation failed." « std::endl; 
return 0;
Handle(Geom Curve) aCurve = anApproximator.Curve();

十七、曲面插值

OCCT 支持使用输入点表进行表面插值：

// Table of points.
TColgp_Array2OfPnt aPnt(lz 3Z 1, 3);
// Fill points.
// Run interpolator.
GeomAPI_PointsToBSplineSurface aSurfMaker(aPnt); 
if (!aSurfMaker.IsDone()) 
{
std: :cout « "Error: Surface construction error** « std: :endl; 
return 0;
Handle(Geom_BSplineSurface) aBsplineSurf = aSurfMaker.Surface();

十八、曲线上的投影

OCCT包含多种投影算法，例如曲线上的点投影或曲面上的投影曲线。与插值算法不同，有时投影不存在：

在这里插入图片描述

十九、曲面上的投影

点不仅可以投影到曲线上，还可以投影到曲面上。下面的代码演示了这一点功能：

// Prepare surface.
Handle(Geom_Surface) aSurface =...;
// Project point on surface.
gp_Pnt aPnt = ...;
// Project point on surface.
GeomAPI_ProjectPointOnSurf aProjector;
aProjector.Init(aPnt, aSurface);
gp_Pnt aNPnt = aProjector.NearestPoint();

有时，存在多个预测，在这种情况下，有必要迭代候选者以专注于解决方案。

const Standard—工nteger aNbSol = aProjector.NbPoints();
for(Standard_Integer anldx = 1; an工dx <= aNbSol; ++an工dx) 
{
gp_Pnt aSol = aProj ector.Point(anldx);
}