基于预测与多样性保持机制的动态多目标进化算法研究（二）——基于预测策略的动态多目标进化算法 之 种群预测策略PPS

 一、概要

Aimin Zhou等人于2013年提出了一 种基于种群的预测策略（PPS，population prediection strategy）。在此之前，预测方法主要用于预测一些孤立的个体， 而种群预测策略是在环境变化后， 根据环境变化之前的一些重要的历史信息来重新初始整个种群中的所有个体。 在该预测策略中，Pareto解集主要包括两个部分： 中心点和副本。中心点的集合主要是用于预测下一个中心点， 而先前的副本主要是估计下一个副本。

二、基本原理

PPS的主要思想就是利用一些历史信息来预测和初始化一个种群， 使它接近新的PS。 首先把一 个种群分成两个部分：中心点和副本， 然后分别对中心点和副本进行预测和估计得到新的种群。 假设在t时刻时， 把分成中心点和副本：

中心点可以根据如下公式评估

  

其中 是的基数。每个点∈ 可以表示为

   

然后

                                                                     

对于中心点和副本有不同的操作策略。对于前者,中心点自然形成一个时间序列。这样,我们可利用这些中心点来预测下一个中心点。对于后者,通过前面的POS副本来估计。这一我们就得到一个近似的初始种群。

                                                   

三、具体方法

接下来的部分给出了估计和的具体过程,并推导出了下一时间步骤产生新种群的方法。

（一）PS中心预测

在t+1时刻,PPS的中心点序列,其中M为序列的最大长度。利用AR模型（单变量自回归）模型来预测下一个中心点。下面我们简单介绍一下AR模型以及模型参数的计算。
令，则下一个中心点可由下列各分量的AR ( p )模型公式估计为

                                                             ，         (4)

其中λ j,i是AR (p)模型的参数,是方差为,i = 1,2,..,n,j = 0,1,..,p - 1的白噪声,p是AR模型的阶数.

                                                          

把历史的中心点，k=0,1,…,M−1代入(4)，得到矩阵公式:

                                                                  

其中i= 1,2,…,n。AR(p) 模型的系数有效向量(i=1,2,…,n) 可以通过使用最小二乘回归方法计算为

                                                              

方差被估计为平均平方误差
                                                      

（二）副本预测

下面介绍PPS如何预测副本的过程：

通过最近的两个副本和来估计PS流形。更具体地说,每个点用来估计一个新的点为

                                                                         (6)

其中。变量 的计算公式为

                                                         

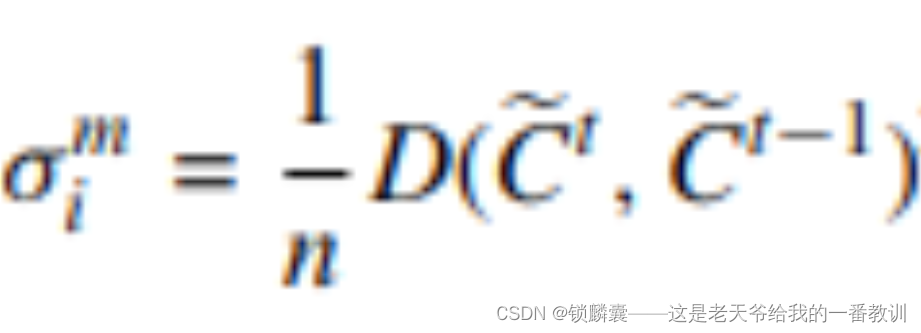
D( A、B)度量副本A和B之间的距离定义为

                                                      

其中| A |是A的基数,| | x-y | |是x和y之间的欧氏距离.很明显,每个点和每个维度的方差都是相同的。可能还存在其他方法来度量两个PS流形之间的相似性,并估计其方差。由于( 6 )在实现上的简洁性,我们使用( 6 )

（三）PPS算法过程

在预测出整个种群的中心点和副本之后， 现在就要确定环境变化之后如何产生新的种群。 根据预测出来的中心点和副本产生整个种群的具体过程如下假设( 4 )和( 6 )中的噪声是相互独立的。将( 4 )和( 6 )代入( 3 ),我们可以推导出一个方程来预测每个的新位置

                                                              (7)

其中i=1,2,…,~N, ,其中表示白噪声的方差。

希望 (7) 生成的初始种群 {x^t+1} 接近PS^t+1。

现在把PPS算法的过程整合到DMOEA框架中。 当环境发生变化时， 在时间ｔ刚开始时， 它的目的在于重新初始化一个新的种群。PPS的过程可以由算法2-5得到。                                                                                 

在步骤1中,当历史信息不足以建立AR ( p )模型时,我们随机抽取一半种群,并从上一次搜索中重新使用一半种群。在Step3.1中,通过提出的策略预测一个新的解决方案。在步骤3.2中,如果每个新点在边界外,则将其修复为在边界内。