树的最长路径【树形DP】

Date：2022.03.29
题意描述：
给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。
现在请你找到树中的一条最长路径。
换句话说，要找到一条路径，使得使得路径两端的点的距离最远。
注意：路径中可以只包含一个点。
输入格式
第一行包含整数 n。
接下来 n−1 行，每行包含三个整数 ai,bi,ci，表示点 ai 和 bi 之间存在一条权值为 ci 的边。
输出格式
输出一个整数，表示树的最长路径的长度。
数据范围
1≤n≤10000,
1≤ai,bi≤n,
−105≤ci≤105
输入样例：
6
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7
输出样例：
22

思路①：首先，如果边都是正权，找树的最长路径有一个通法——先任意找一点$u$，找到距离u最远的点$x$，在找到距离$x$最远的点$y$。由此，点$x$和点$y$的距离即为数的最长路径（也就是树的直径）。
证明：由于直径是最长路径，因此只需证明$x$是直径的一个端点即可。
反证法：假设$x$不是直径的一个端点，我们先求出来这个直径【假设为$(a,b)$】，此时仍然有两种情况：
(1) 新的直径$(a,b)$不与$(u,x)$相交：

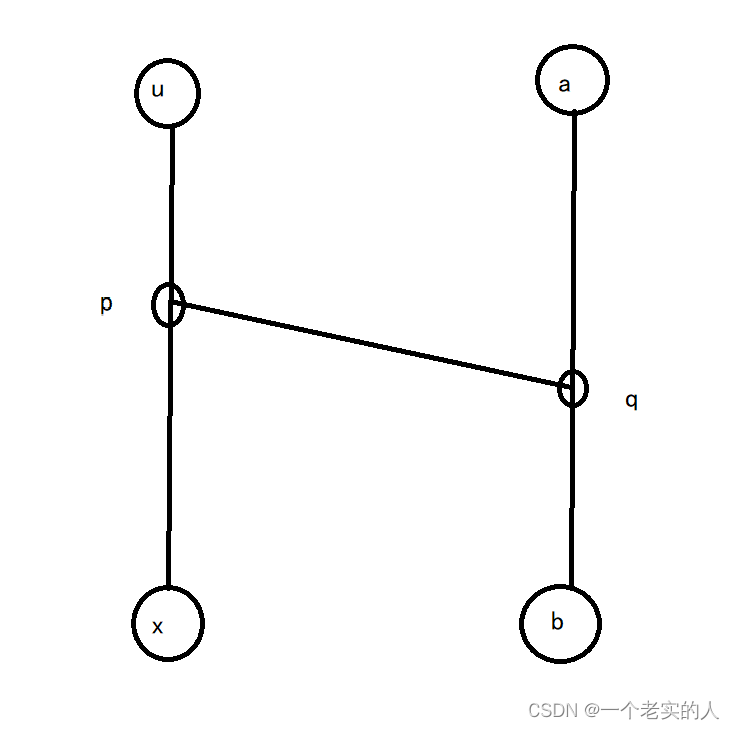
虽不相交，但都在一棵树上能彼此到达。因为$x$离着uu