有向图强连通分量(Tarjan)算法

   在图论中，连通图基于连通的概念。在一个无向图G 中，若从顶点到顶点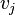有路径相连(当然从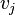到也一定有路径)，则称和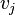是连通的。如果 G 是有向图，那么连接和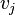的路径中所有的边都必须同向。如果图中任意两点都是连通的，那么图被称作连通图。强连通图指每一个顶点皆可以经由该图上的边抵达其他的每一个点的有向图。意即对于此图上每一个点对(Va,Vb)，皆存在路径Va→Vb以及Vb→Va。强连通分量则是指一张有向图 G 的极大强连通子图G'。这些都是图论的基本概念。

   求强连通分量的算法有两个算法一个是Kosaraju算法 它需要两次DFS过程来实现，另一种是Tarjan,它通过一次DFS就可以找出图中的连通分支。本文就主要介绍Tarjan算法。

   Tarjan算法的原理就是，如果 v是某个强连通分量的根，那么：

• v不存在路径可以返回到它的祖先
• v的子树也不存在路径可以返回到v的祖先

   Tarjan算法的实现就是基于这两个实现， 它用一个dfn[i] 记录顶点i进入栈的时间，也就是在该点进入栈之前已经访问过多少个顶点, 用low[i]表示顶点i或者i的子树能够返回到顶点(栈中)的次序(时间)，low[i]是要在递归过程中不断更新的，下面说一下它的更新原则：

• 如果u是i向下DFS的树边(u没有入过栈) low[i] = min(low[i], low[u])
• 如果u是i向下DFS的横叉边(u已经在栈中) low[i] = min(low[i], dfn[u])

根据上面的原理， 可以发现只有当且仅当low[i] == dfn[i] 正好是连通分量的根，这时我们把根顶点之前的栈中顶点出栈，并且标记好所属的连通分量号。

下面我用poj 1236来当作例子 来给出实现代码， 题意：

   一些学校通过网络连接在一起，每个学校手中有一份名单，即它所指向的点。学校A的名单中有学校B，并不能保证学校B的名单里有学校A。现在有一软件，1.问至少发给几个学校才能保证所有的学校都可以得到该软件。2.至少加几条边才能使将软件发给某个学校后，其他所有学校都可以得到软件。
题解：第一问求的是入度为0的点。第二问求的是加几条边使图变为强连通图。

思路： 

对于问题1：我们只需缩点后求出入度为0的强连通分量个数。

对于问题2：求出入度为0的个数，出度为0的个数，输出较大值即可。

实际上是连通分量 + 缩点+出入度问题：

代码：

#include <stack>
#include <iostream>
#include <algorithm>
#include <string.h>
using namespace std;
const int MAX_N = 110;

struct Edge{
  int u, v;
  int next;
};
Edge edge[MAX_N * MAX_N];
bool in_stack[MAX_N];
stack<int> st;
int dfn[MAX_N], low[MAX_N];
int component[MAX_N];
int comp_num;
int adj[MAX_N];
int edge_num;
int N;
int dfn_num;

void add_edge(int u, int v)
{
  edge[edge_num].u = u;
  edge[edge_num].v = v;
  edge[edge_num].next = adj[u];
  adj[u] = edge_num++;
}

void tarjan(int root)
{
  dfn[root] = low[root] = ++dfn_num;
  st.push(root);
  in_stack[root] = true;
  for(int i = adj[root]; i != -1; i = edge[i].next)
  {
    int v = edge[i].v;
    if(dfn[v] == 0)
    {
      tarjan(v);
      low[root] = min(low[root], low[v]);
    }
    else if(in_stack[v])
      low[root] = min(low[root], dfn[v]);
  }
  if(dfn[root] == low[root])
  {
    ++comp_num;
    while (1) {
      int x = st.top();
      st.pop();
      component[x] = comp_num;
      in_stack[x] = false;
      if(x == root)
        break;
    }
  }
}
int main()
{
  cin >> N;
  int x;
  edge_num = comp_num = dfn_num = 0;
  memset(adj, -1, sizeof(adj));
  for(size_t i = 1; i <= N; ++i)
  {
    while(cin >> x && x != 0)
      add_edge(i, x);
  }
  memset(in_stack, false, sizeof(in_stack));
  memset(component, 0, sizeof(component));
  memset(dfn, 0, sizeof(dfn));
  for(size_t i = 1; i <= N; ++i)
  {
    if(dfn[i] == 0)
      tarjan(i);
  }
  if(comp_num == 1)
  {
    cout << 1 << endl;
    cout << 0 << endl;
    return 0;
  }
  //一定注意要申请大于N大小的数组 因为在特殊数据情况下连通分量的个数就等于顶点个数N，而又是从下标1开始算起的
  int out[N + 1], in[N + 1];
  memset(out, 0, sizeof(out));
  memset(in, 0, sizeof(in));
  //缩点， 将属于同一连通分量的点缩成一个点重新建立一个有限无环图并统计每个点的出入度
  for(size_t i = 0; i < edge_num; ++i)
  {
    int u = component[edge[i].u];
    int v = component[edge[i].v];
    if(u != v)
    {
      out[u]++;
      in[v]++；
    }
  }
  int res1 = 0, res2 = 0;
  for(size_t i = 1; i <= comp_num; ++i)
  {
    if(out[i] == 0) res1++;
    if(in[i] == 0) res2++;
  }
  cout << res2 << endl;
  cout << max(res1, res2) << endl;
  return 0;
}