专栏总目录
2.2概率与统计
我们总结过去已经存在的数据,就是在做统计;而概率则是根据已知的观察,去推测未来发生某事件的可能性。
语音识别中,一监督为主的机器学习算法,都是基于已知数据的训练和学习,其中最根本的就是统计语音数据的概率和特征,从而实现语音的自动分类。
2.2.1 概率基础
概率是在不确定的情况下,对某个事件结果发生可能性的描述。一般将事件抽象为一个随机变量,随机的意思就是直到结果发生的那一刻,才能确定该事件发生的结果。如:抛一枚硬币,在落地之前,你无法直到它是正面朝上还是反面朝上。
当我们将抛硬币时间描述为一个随机变量时,其结果可能是正面朝上,也可能是反面朝上,这两种结果是随机的,对于这种不确定的情况需要引入概率。也就是说,这两种结果都是以某种概率发生大的。经过无数实验证明,随着抛硬币次数的增多,每种结果发生的概率会趋近于1/2,并且两者的概率之和等于1。
因此我们可以得出概率的第一个性质,就是单个随机变量x的所有结果发生的概率之和等于1。比如在抛硬币事件中,可以有下列概率关系:
P(x = 正面) = 1 - P(x - 反面),其中P(x = 正面) = 1/2
实际应用中,求取一个结果发生的概率不是目的,而是希望知道所有结果的概率分布情况。
(1)概率分布
根据随机变量的取值是否连续,可以分为离散型随机变量和连续型随机变量。
A. 离散型随机变量的概率分布
仍以抛硬币为例,其可能有两种情况:正面朝上或反面朝上(注意:我们不考虑直立的情况)。现在我们将硬币抛了10次,记录的结果为正面6次,反面4次。那么,就相当于P(x = 正面) = 0.6 ,P(x = 反面) = 0.4。画出图来,概率结果如下图所示:
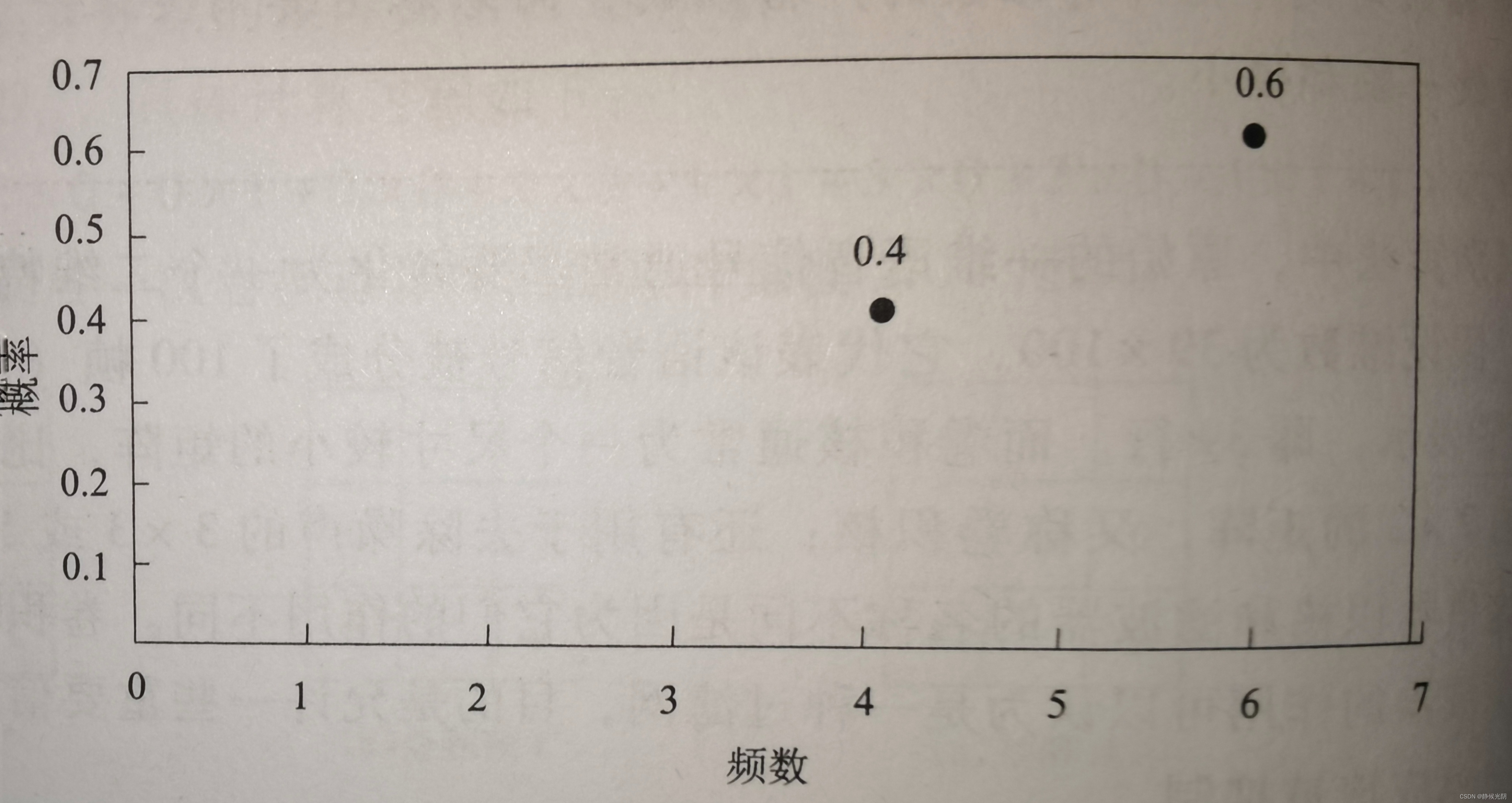
从上图不难看出概率分布只有两个离散值,即频数等于4时的0.4和频数等于6时的0.6。这种概率分布便是离散型随机变量的概率分布。
B. 连续随机变量的概率分布
除了离散值的情况,还有一种更常见的情况是随机变量的值是连续变化的。
如下图所示,某地区成年女性的升高统计。由于样本量大,导致横坐标的身高分布形成了一条含有多个波峰和波谷的连续曲线。其中在160cm附近的人数最多(即圆圈重点标注的部分),说明该地区女性的平均身高大约为160cm。
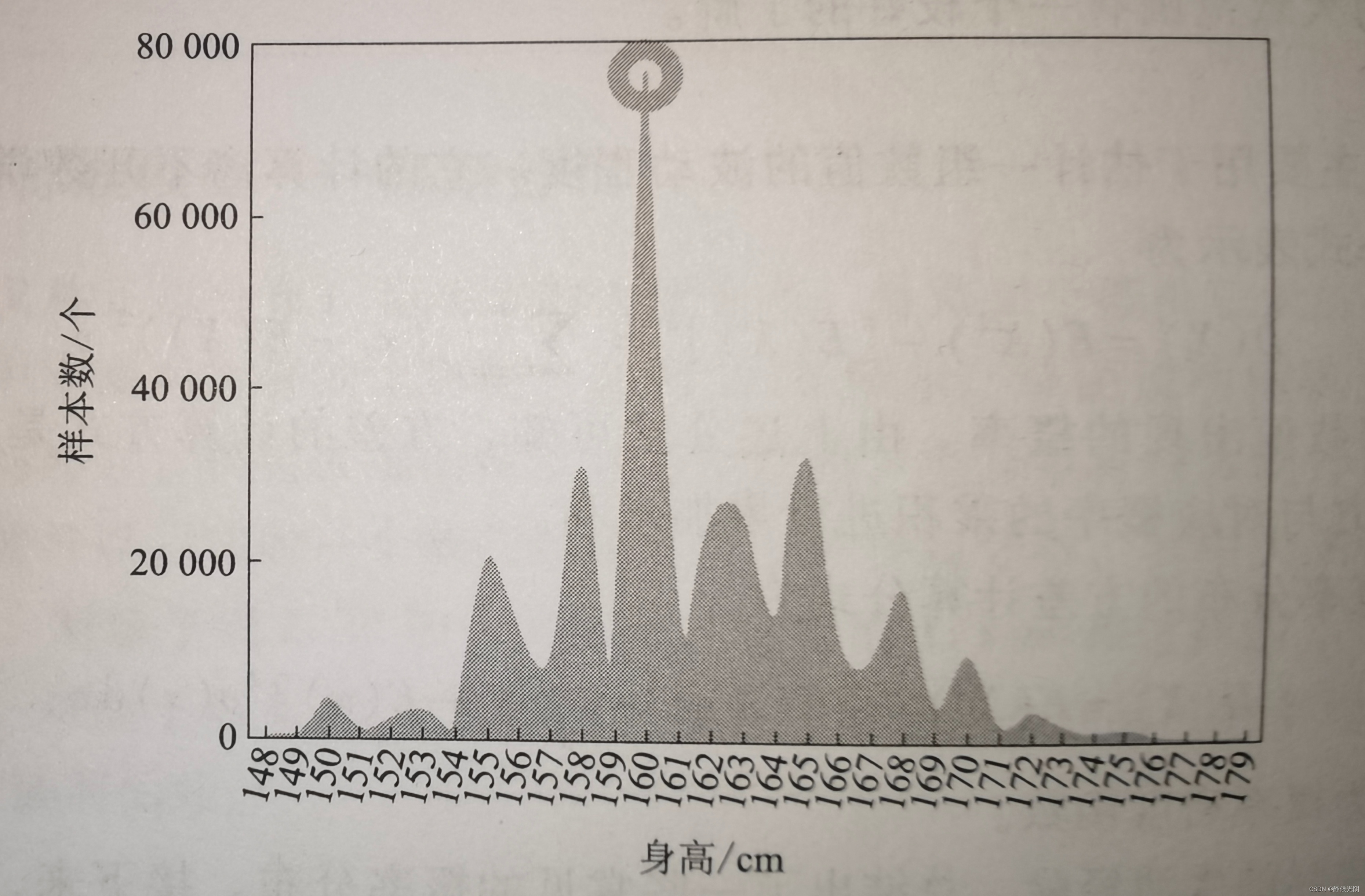
由此可见,连续性随机变量的概率分布往往是曲线形式。幸运的话,这种曲线的趋势还可以被表示成一种特定的函数,比如高斯函数。
了解概率的分布后,我们还会希望做一些统计分析,从而分析出数据的一些重要特征。最常见的统计分析就是数学期望和方差。
(2)数学期望
数学期望又称均值,简称期望,它反映了随机变量的平均取值大小。
对于离散型分布的数据来说,期望值的计算方式是概率的加权平均,如下图:
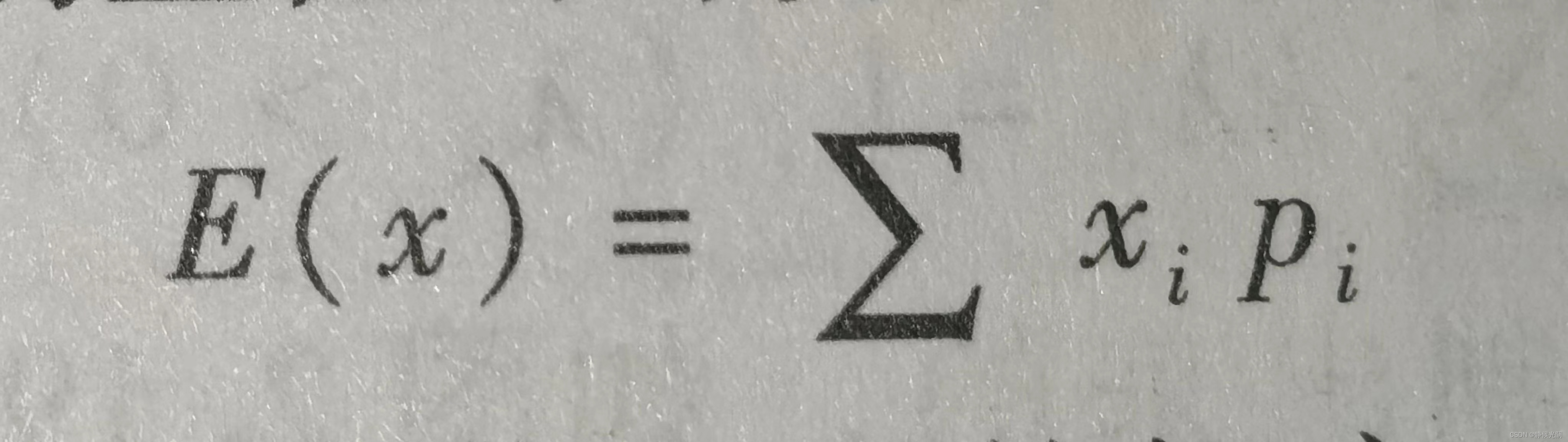
其中,xi是随机变量的取值,pi是每个取值出现的概率。
举例:
随机选取某市1000个家庭,统计孩子的数量x,x可能的取值为0,1,2,3,其中,300个家庭没有孩子(x = 0),500个家庭仅有一个孩子(x = 1),150个家庭有两个孩子(x = 2), 50个家庭有三个孩子(x = 3)。最终得到被统计家庭孩子的数量见下表:

根据上图可知,1000个家庭有孩子的数学期望值的计算式为:
E(x) = 0 x 0.3 + 1 x 0.5 + 2 x 0.15 + 3 x 0.05 = 0.95
由于上述结果式0.95,但是实际上孩子的个数都是整数,因此,我们取近似值1,于是,该期望值说明现在该市每个家庭平均有一个孩子。
对于连续型分布的数据来说,期望值要通过积分公式求取:
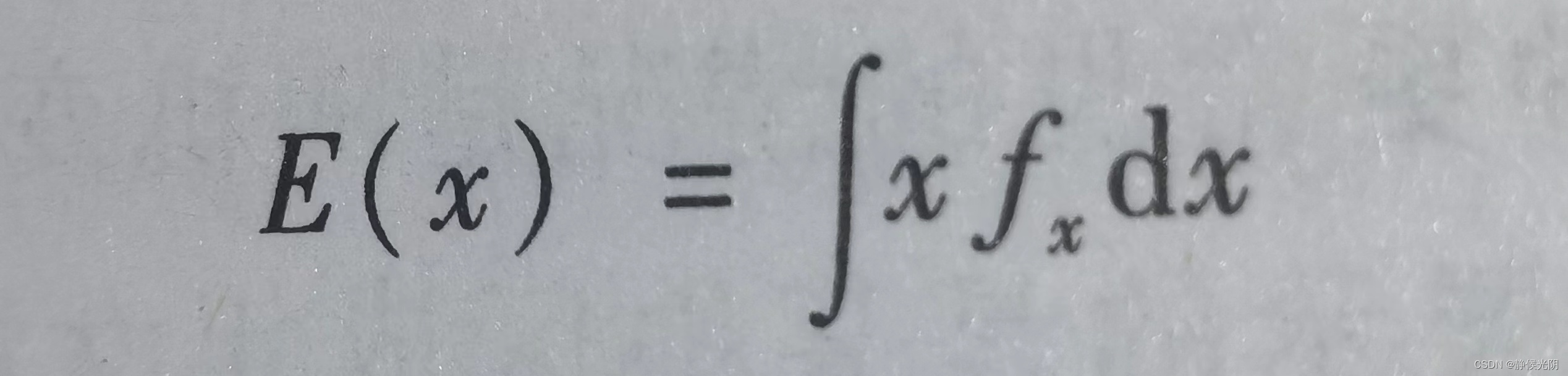
其中,x是随机变量;fx是概率分布函数,它的作用是描述随机变量取特定值的可能性。
期望值对于分析一组随机变量的平均值非常有用,通过计算期望值可以推测出一个具体的结果大概率处于平均值的哪个范围。期望常常用于对语音数据的一些初步探索分析,便于对数据取值的大致范围有一个较好的了解。
(3)方差
方差D(x)主要用于估计一组数值的波动程度。它的计算离不开数学期望。其中,离散方差的计算公式表示为:
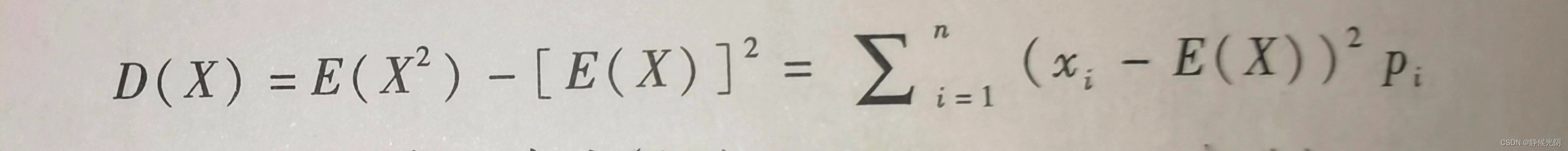
其中,Pi是每个数值出现的概率。由上述公式可知,方差的计算方式是每个数xi,与预期E(x)之差的平方与对应概率的乘积进行累加求和。
而连续型概率分布的方差计算公式为:
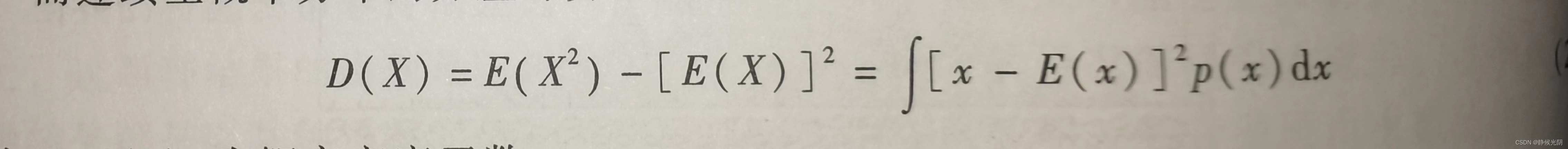
其中,p(x)为概率密度函数。
人们根据实际的生活经验,总结出了一些常见的概率分布。我们了解以下在语音识别应用中最多的两类概率分布:分类分布、高斯分布
2.2.2 分类分布
分类分布是离散分布中的一种,它表示一个具有k个不同结果的单个随机变量的分布。其中k是有限的数值,并且第k个结果对应着一个概率 入k:
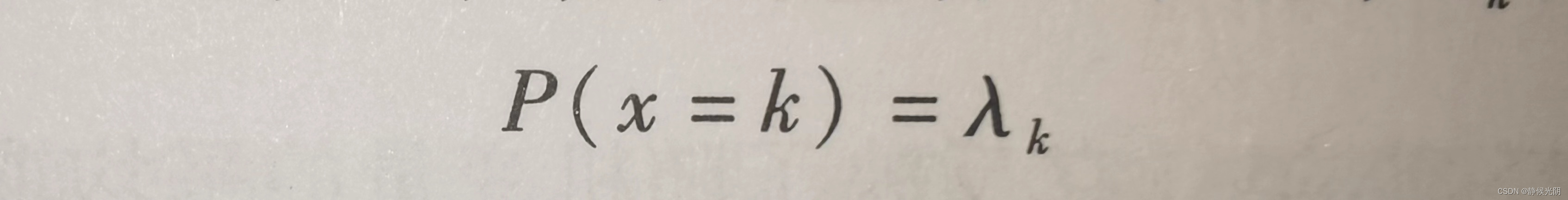
其中分类分布的特点服从式如下图,每一类取值的概率大于0,并且总的概率之和等于1。
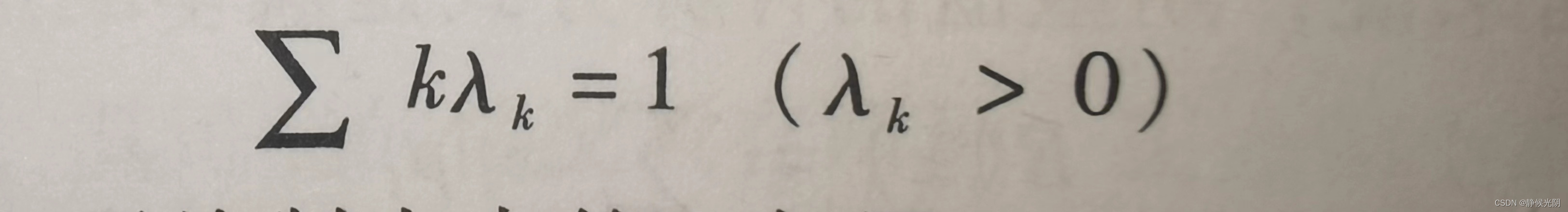
分类分布是可以通过直方图绘制出来的,如下图所示:
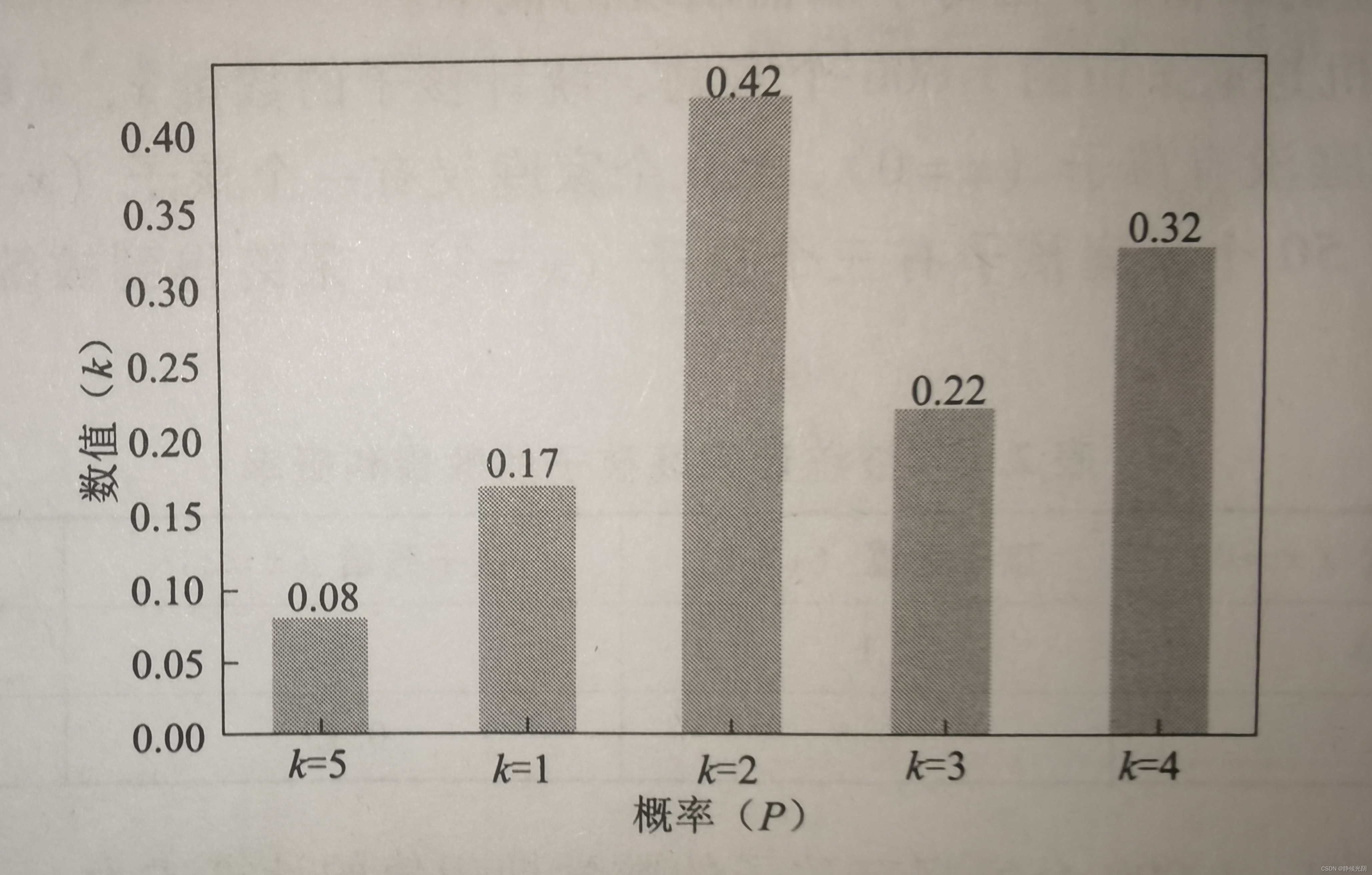
分类分布在语音识别中的应用:
分类分布主要用于语义词典的概率统计。一般来说,一个确定的语言体系通常是由确定数量的单词构成的,那么每个单词在句子中出现的概率是可以统计出来的,即通过统计单词出现的频次,得出其对应的概率值。
这就构成了离散分布中分类分布的基础,k对应着单词的数量,P(x = k)代表某个单词出现的概率。一旦给出确定的大量句子数据,那么每个单词的分类分布就可以很容易计算得出。
2.2.3 数据的标准模型——高斯分布
高斯分布(又称正太分布)是典型的连续分布,是指某个随机变量的概率分布曲线的外形,好像一个中间高两边低的太阳帽,如下图所示。该图说明随机变量的取值大多数都集中在中间的部分,两边极端的情况是极少数的。
生活中有很多统计数据的分布都基本符合正太分布的特点,比如一个地区的成年男性的身份分布,其中大多数男性的身高都为1.63~1.70m,对应于下图的中间部分,过矮1.3m和过高的2.3m都属于极端情况,概率很小,对应于下图中两侧的帽檐。类似地,女性身高的平均值1.5吗,对应于图2.20中较矮的曲线。
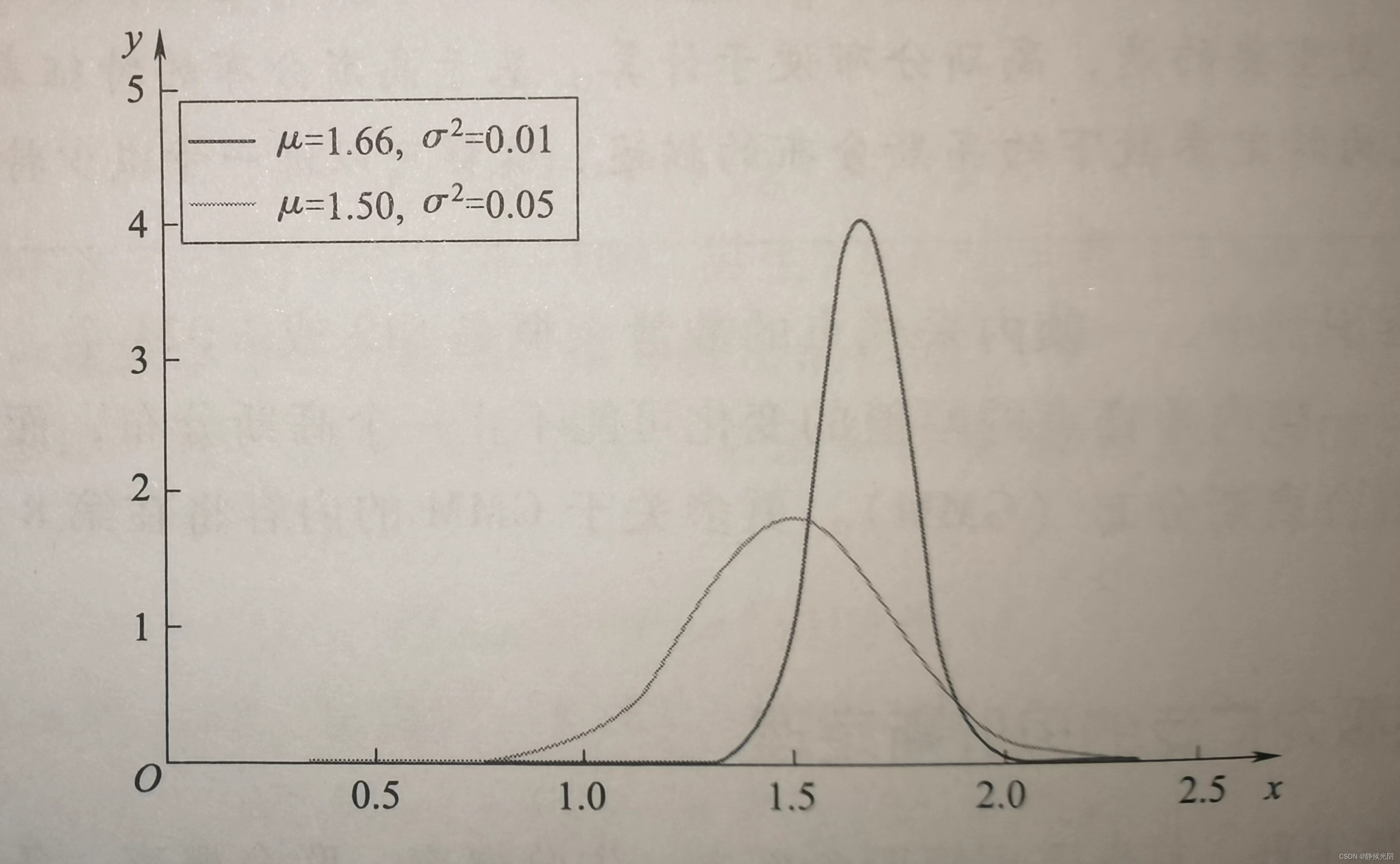
高斯分布的概率密度函数为
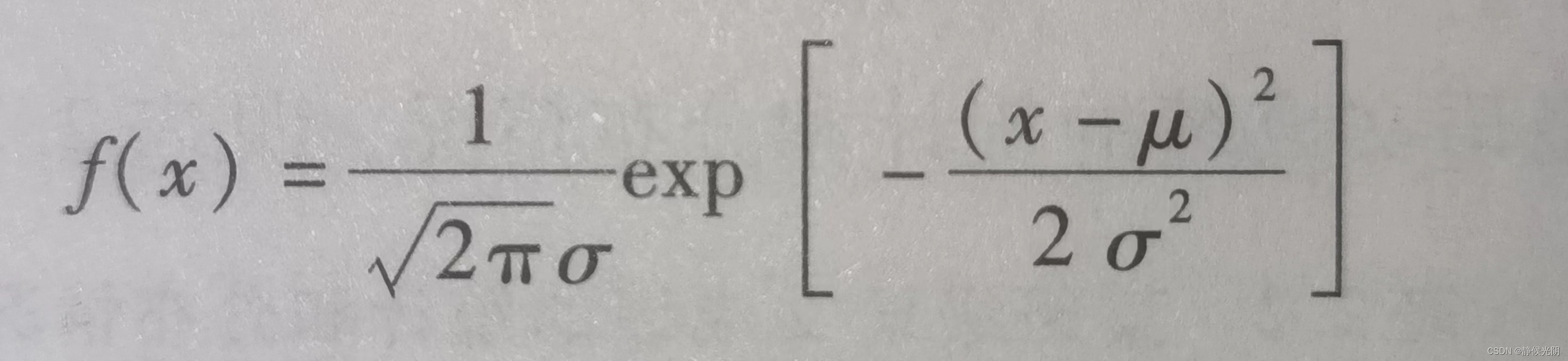
其中,f(x)是关于随机变量x的函数,x的取值服从高斯分布;u的含义可以理解为x所有取值的平均值;a表示所有取值的标准差。结合上图可知,u值表示随机变量x的平均值对应横坐标的位置,不同的a值则对应帽檐的形状,即标准差。x的取值取值越极端,离平均值就越远。
一组数对应的高斯概率分布可以通过参数(u, a)确定下来。下图所示,不同的均值(m)和标准差(sig)对应不同形状的高斯分布曲线。
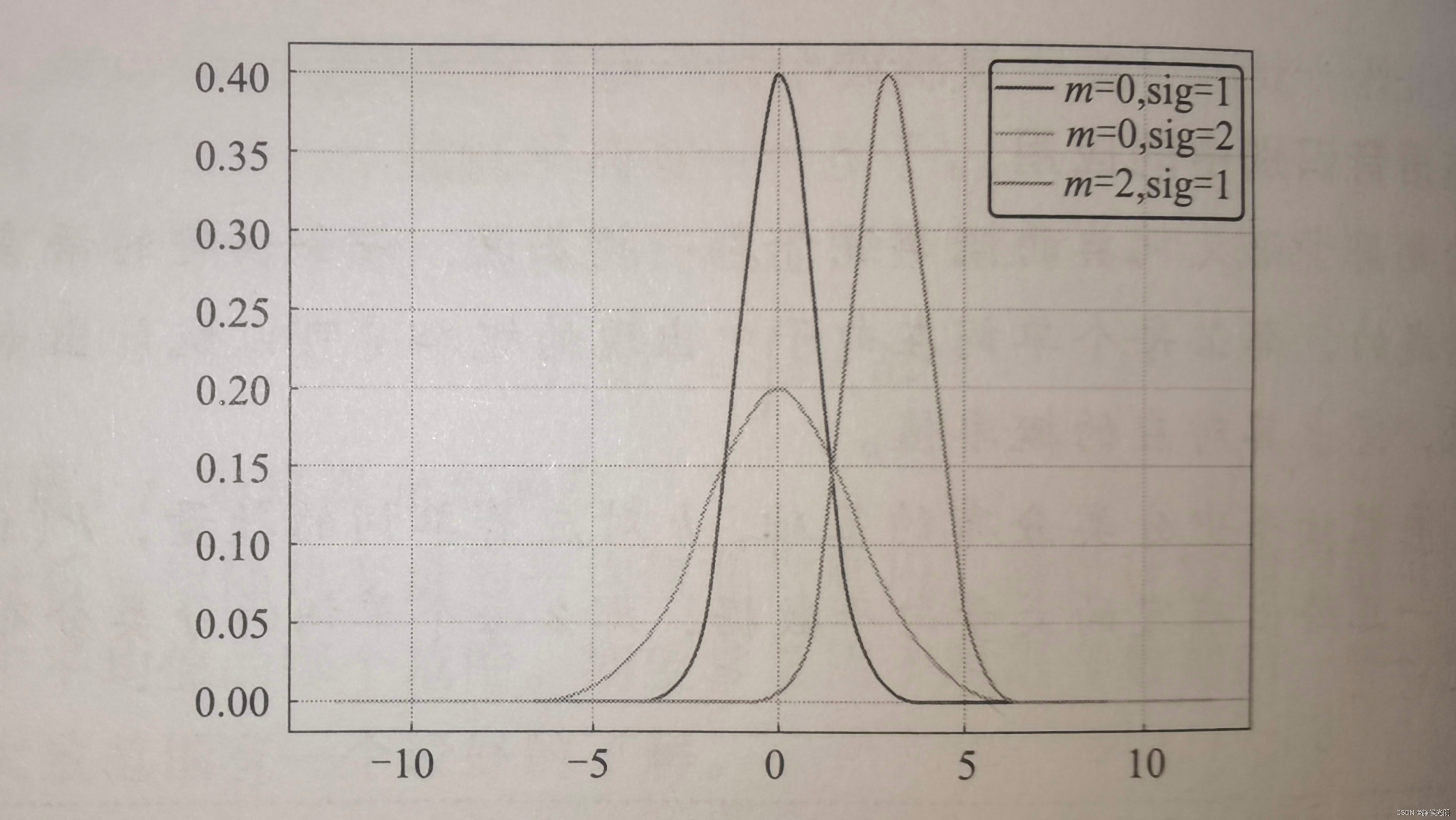
高斯分布在语音识别中的应用
在语音识别中,当分析一组特征向量的值时,常常假定向量中特征值的分布时符合正态分布的,因此,需要确定的只是通过训练得出正态分布的两个参数(均值和标准差),从而确定该向量可能对应的音素或状态。比如一个静音帧和一个元音帧的高斯概率分布一定是不一样的。
具体地,当我们针对一帧以内的采样点计算特征量后,这些特征向量的值假设符合高斯分布。做出这种假设的主要原因是高斯分布是数据分布中最常见的,因此,可以保证出现意外的可能性低。更重要的是,高斯分布便于计算。基于高斯分布的特征表示,将一帧内的采样点的幅值转化为特定参数下的高斯分布的描述,这样可以进一步减少特征向量的维数。
在实际的语音识别中,一帧内采样点的数量大概是512或1024个。人们对语音信号的特点的研究发现,一帧内采样点的幅值的变化可能不止一个高斯分布,而是多个高斯分布的组合,这就是混合高斯分布(GMM)。更多关于GMM的内容将在第八章。
2.2.4实用性极为广泛的贝叶斯定理
要理解贝叶斯定理,首先要理解四个概念:先验概率、联合概率、条件概率和后验概率。为了更好地理解四种概率,将他们融入一个例子中:
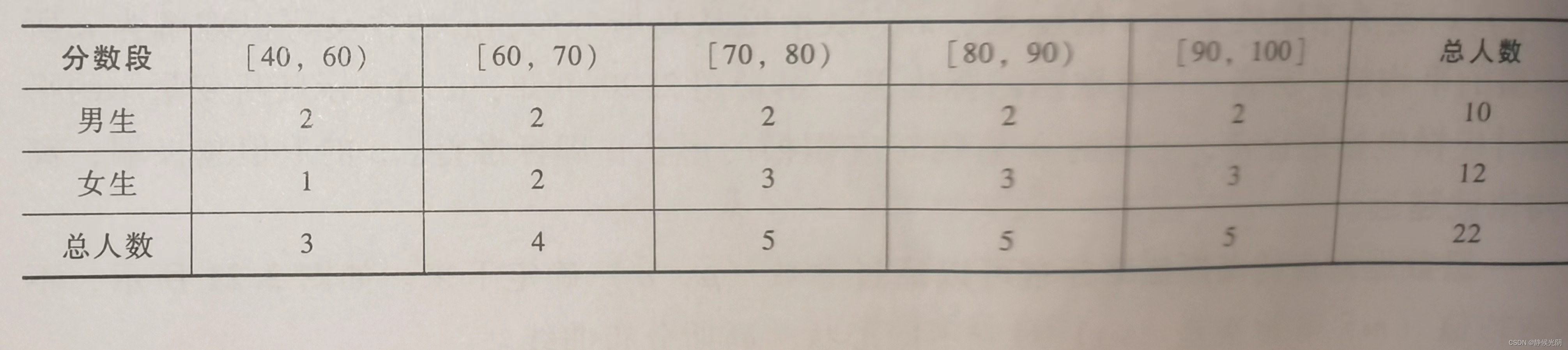
假设现在直到某班语文乘积的统计和分布情况,见下表:
(1)先验概率:根据已知情况,直接得到的概率
根据上表,可以定义两个随机变量,一个是语文乘积的分数段s,一个是学生的性别g。我们可以很容易得出这个班级中男生的概率是P(g = 男生)= 10 / 22 = 0.45。90分及以上的学生概率是P(s = 90~100)= 5 / 22 = 0.22。这两个概率都是根据表中的已有数据直接求出的,称为先验概率。
(2)联合概率:以两个随机变量s,g的联合概率为例
接下来,请计算:全班考了90分以上的男生的概率是多少?
分析一下,该问题要求的概率涉及两个随机变量s和g。因此,要求出这个概率,就要用到这两个随机变量组成的联合概率,可以表示为联合概率P(s, g),这个概率同时满足以下两个条件:
A. s 在[90, 100]的范围
B. g = 男生
(3)条件概率:当部分条件发生时,构成条件概率
为了计算上面的联合概率,还要用到条件概率
根据上表可知,P(s = 90~100 | g = 男生) = 2 / 10 = 0.2。与之前求得的先验概率不同的是,这个概率时在性别变量为男生条件下发生的,乘积分段为 [90, 100] 发生的概率,这种概率就是条件概率。
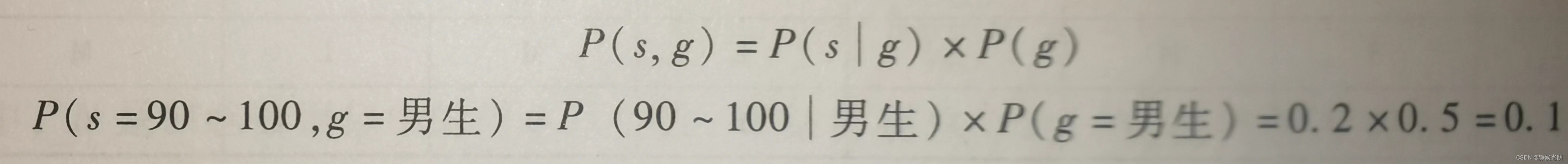
(4)后验概率:根据前面三种概率,推到得出的概率
为了将上面条件概率的式子推广到更多的情况,它还可以变形为下列式子,计算结果一样。
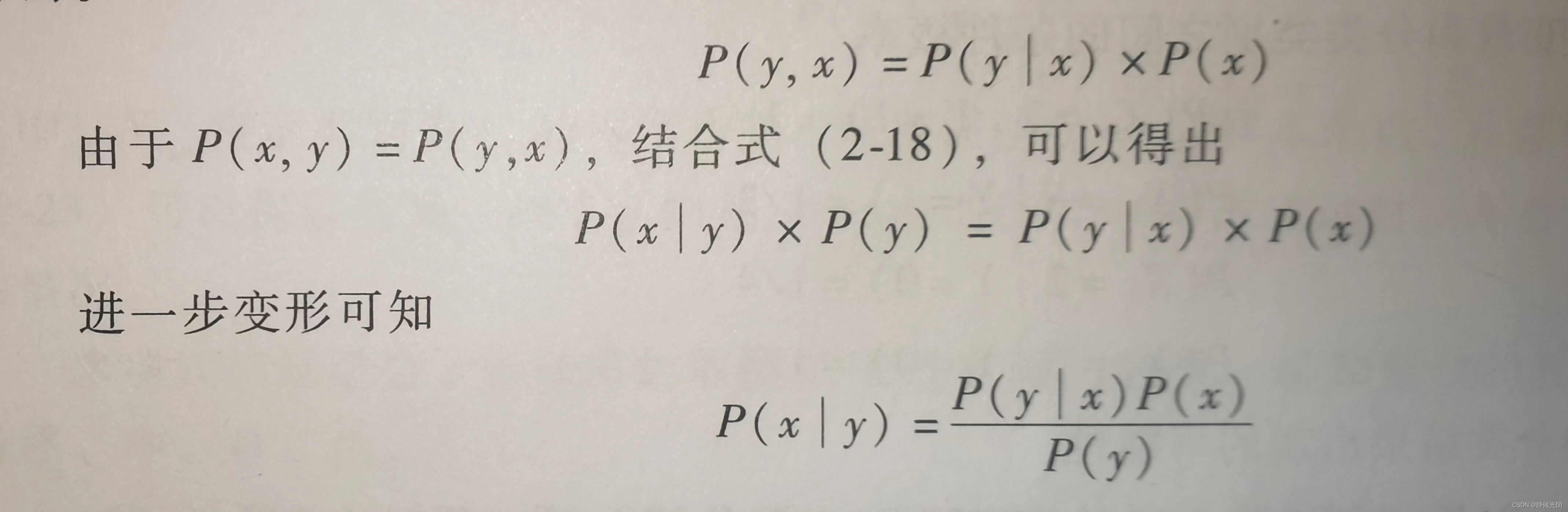
其中导数第二部就是贝叶斯定理的核心公式:
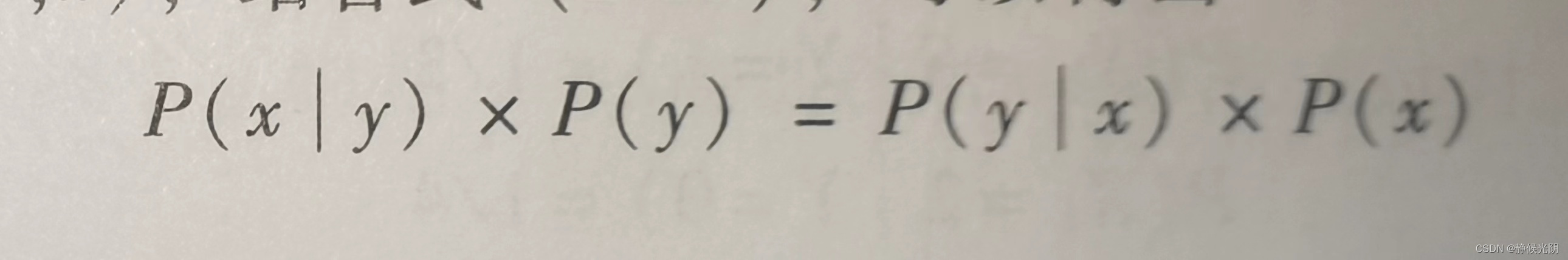
该公式的灵活性体现在,可以通过某一个随机变量(比如y的先验概率,以及随机变量x的先验概率和条件概率)得到在y的条件下x发生的后验概率P(x | y)。对应上面的示例,就是说,得到了已知在成绩分段为 [ 90 ~ 100 ] 的条件下,性别变量为男生发生的后验概率P(g = 男 | s = 90~100)。
根据除法分式的规律,如下式子
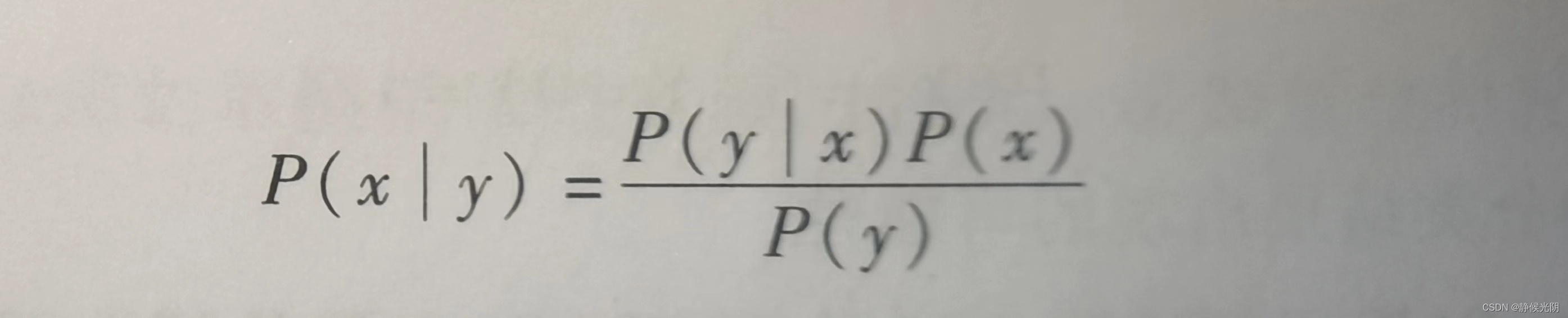
可以变形为:
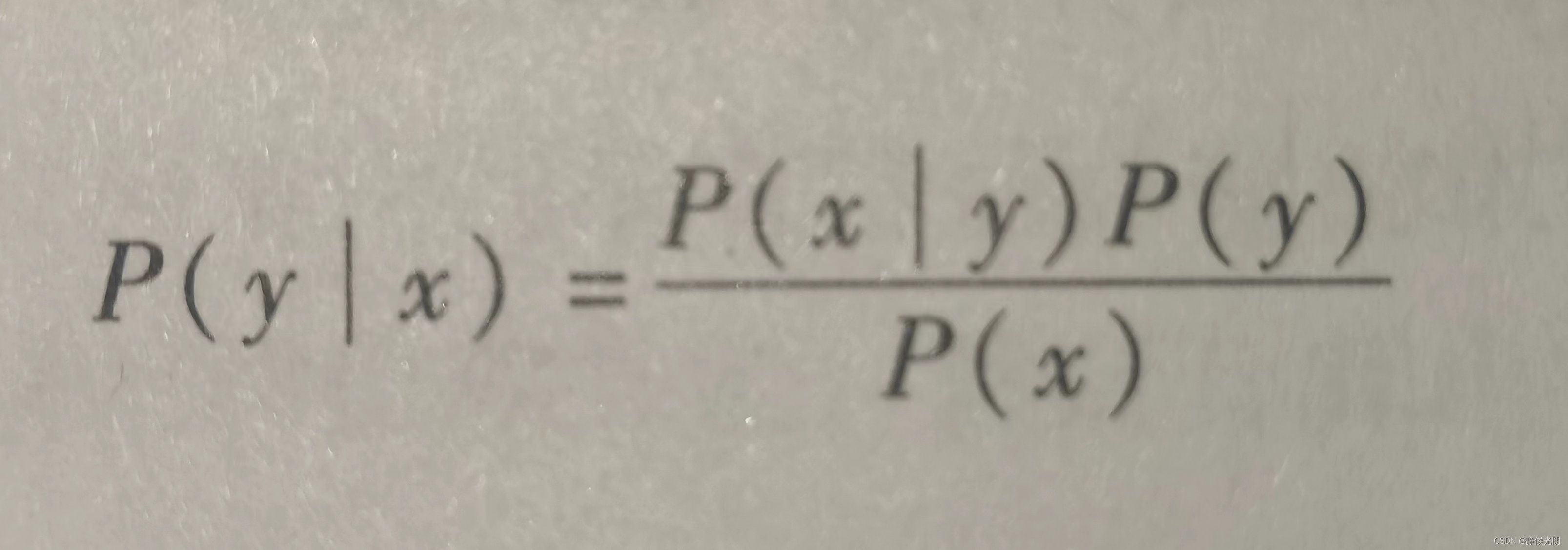
两个公式选择取决于哪一个条件概率更好计算。
当条件不好计算时
在介绍贝叶斯定理时,提到P(y | x)是给定x之后,y出现的条件概率,可见,这里我们已经直到了通过模型的参数来预测结果。然而,很多实际情况是,我们并不知道数据的模型,因此,更多的是采用似然函数L(y | x),它是指根据观测到的结果数据来预估模型的参数。当y值给定时,两者在数值上是相等的,在应用中可以不用细究。
(5)贝叶斯定理的应用示例
贝叶斯定理推导过程,主要借助四种基础概率相互推导得来的。
举例看一下它在语音识别中最常见的一类应用——样本数据的分类。
假设已知有七个训练样本数据,每个样本数据都是由一组二维特征向量(X1, X2)表示的,其中X1表示样式类别,取值是1或2;X2表示尺寸,取值是S, M 或L。这些样本对应的类别Y为两个值,其取值为0和1.对于给定的测试样本 x = (2, S)T,具体的训练数据情况见下表:

A. 计算分类类别的先验概率(P(Y))
P(Y = 1) = 3 / 7 P(Y = 0) = 4 / 7
B. 计算随机变量和分类类别之间的条件概率
P(X1 = 2 | Y = 1) = 1
P(X2 = S | Y = 1) = 1 / 3
P(X1 = 2 | Y = 0) =1 / 4
P(X2 = S | Y = 0) = 1 / 4
C. 求每一种分类结果出现的可能性
P(Y = 1)P(X1 = 2 | Y = 1)P(X2 = S | Y = 1) = 0.143
P(Y = 0)P(X1 = 2 | Y = 0)P(X2 = S | Y = 0) = 0.035
最终,比较上述两个概率结果的大小可知,基本判定测试样本很有可能是Y = 1所代表的类别。
总结上述示例可知,在分类问题中,贝叶斯定理主要从概率的角度除法,对未知样本的类别判断,常常可以转化为求解P(y1 | x)和P(y2 | x)中概率值最大的那一个,即求后验概率值最大的输出:argmaxP(yk | x)。
贝叶斯定理是一个通用模型
贝叶斯定理是一个很广泛且通用的模型,说它通用是因为它可以指导我们得出一些有意义的结论,并且具有一定的科学性支撑。但是,由于它的宽泛性,导致它并不是给出了一个具体的概率模型,也就是说,具体到一个问题,这个概率P它到底是采用朴素贝叶斯模型还是高斯模型,贝叶斯定理并没有明确给出(注意,这里的模型相当于一个具体的概率分布函数)。
实际上,在遇到具体问题是,情况会复杂得多。比如在上述分类示例中,我们只用到了两个随机变量作为描述数据的特征向量,而在实际问题中,往往涉及多个维度的特征向量,当然无论特征向量的维度是多少,后验概率的计算方法都是类似的。但是在具体应用中,还需要考虑特征值是离散的还是连续的,特别地,特征值是否连续决定了采用的概率模型P也不尽相同。
(6)贝叶斯定理中具体模型的确定:离散概率模型和连续概率模型
接下来针对离散型和连续多维特征向量介绍适用于他们的典型的概率模型
A.适用于离散型多维特征向量的朴素贝叶斯模型
关于离散型的多为特征向量,常常采用多基于多项式模型的朴素贝叶斯方法。其思想是在计算贝叶斯公式中右侧分母的P(yk)时,需要适当地做一些平滑处理,避免某些之的概率为0,导致公式计算失败。因此,当特征向量为1维时,P(yk)的计算式为:
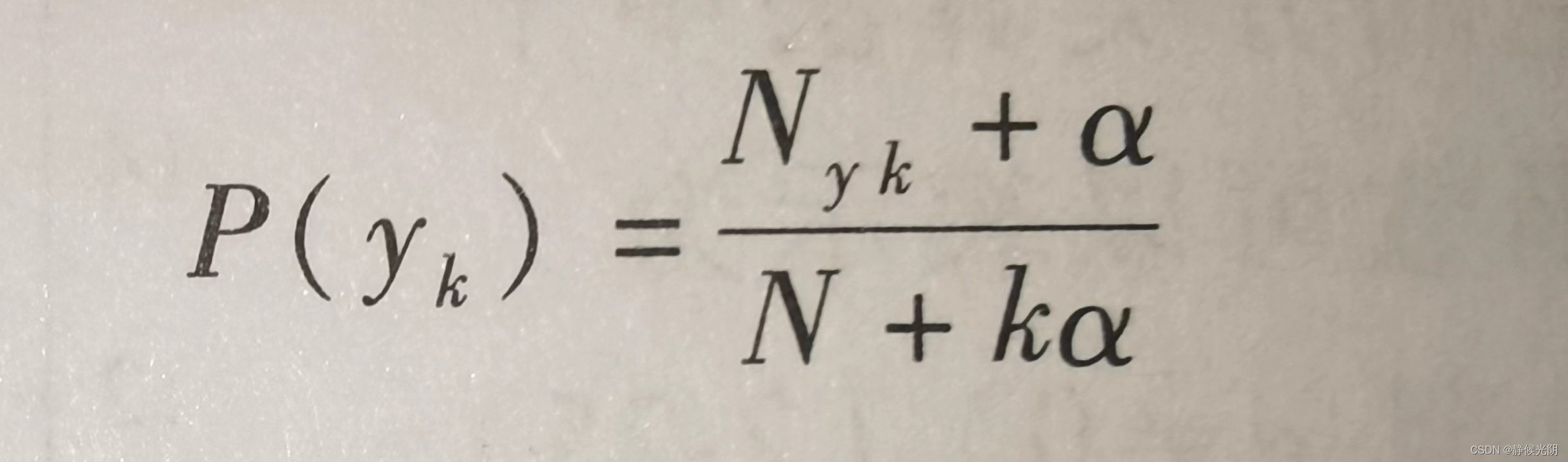
其中,N是训练数据集中的样本总个数;k是类别总个数;Nyk是类别为yk的样本个数;a是平滑值,一般范围为(0~1),当a = 0时,表示不做平滑。当特征向量维数大于1时,P(yk)的计算式为:
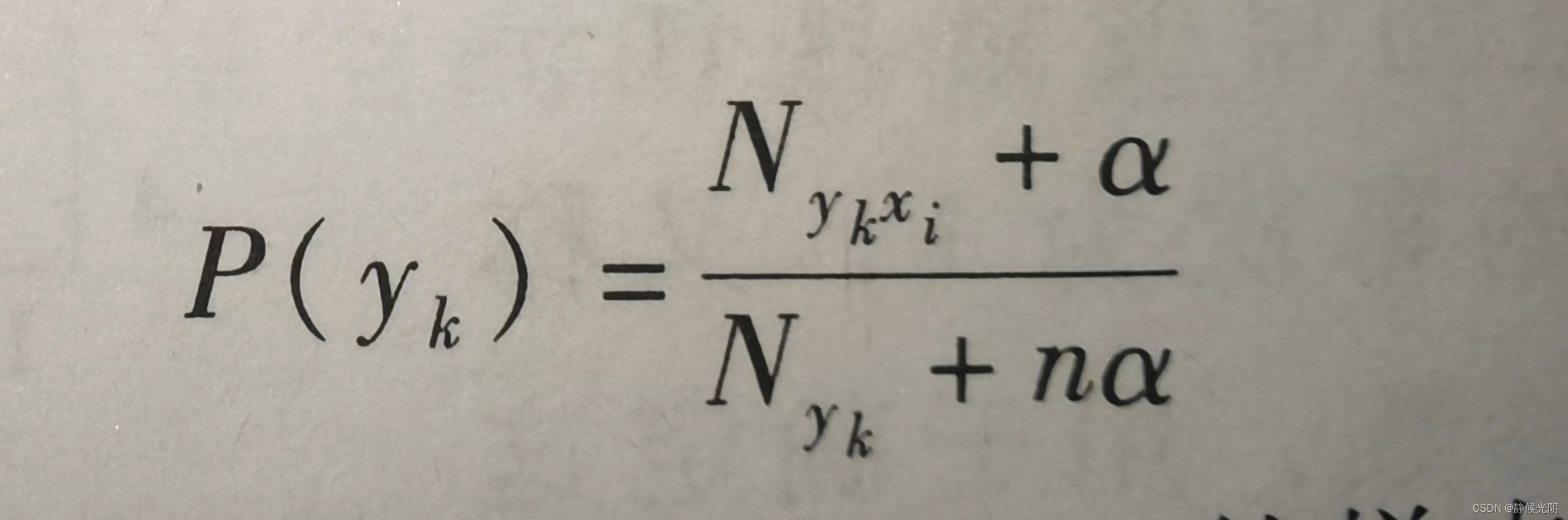
其中,Nykxi表示类别为yk的样本中第i维特征值是xi的样本个数,n是特征的维数。上述公式可以保证当某一维特省的值xi未在训练样本中出现过时,不会出现后验概率为0的情况。
多项式模式适合于特征值的取值范围是有限的数量。比如成绩的五个分段:不及格、及格、中、良、优。
B. 适用于连续型多维特征向量的高斯模型
关于连续型的多维特征向量,常常采用高斯模型比如身高和体重的变化。
例如:某地区男性身高的高斯概率分布可以通过下列式子求得,最终得出的结果说明该地区男生的平均身高在1.58m附近。
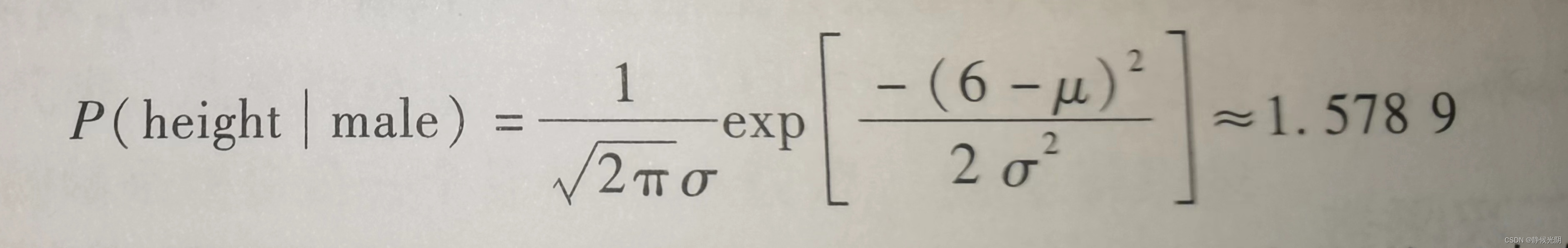
一般来说,常常假设多为特征向量中的所有特征分量的取值都服从正态分布。于是可以统计出训练样本中每一个特征分量的均值和方差,然后计算出某一个测试样本值的概率。
人的大脑也许就是贝叶斯概率应用的典型
以前,语音识别主要是根据人们制定的语法规则将识别出的单词组成句子,然而人类交流的实际情况是,语言的语法规则是很晚才出现的,在此之前,人们就能顺畅交流。后来由google的专家贾里尼提出应该用统计和概率的方法,这才让语音识别的准确率得到了很大的提高。
试想一下,当你和朋友聊天时,当对方说出“今天感觉很冷”,你知道对方是在说天气。尽管这句话从语法上说,缺少主语“我”,但是这也不妨碍你的理解。于是接下来,很大概率上你会做出与天气相关的回应。这就说明人的大脑大概率也是贝叶斯概率的体现。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










