题意:
给你一棵树, 让你求这棵树上满足dis(u, v) <= k的点对有多少个。
分析:
首先, 对于直接想到的办法。lca预处理然后暴力,复杂度n^2,显然复杂度太大。 那么我们就有了树上分治的思想;
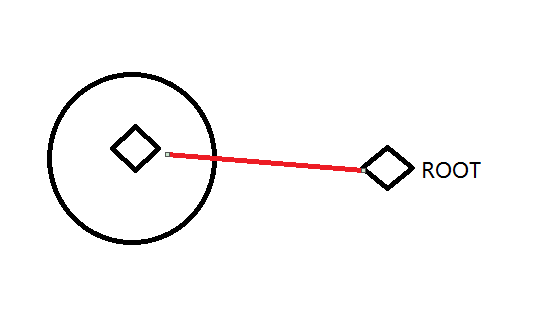
首先, 对于这个问题, 我们可以看出只有如下三种情况:
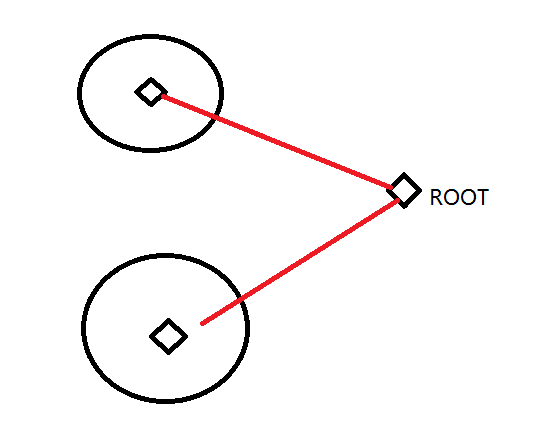
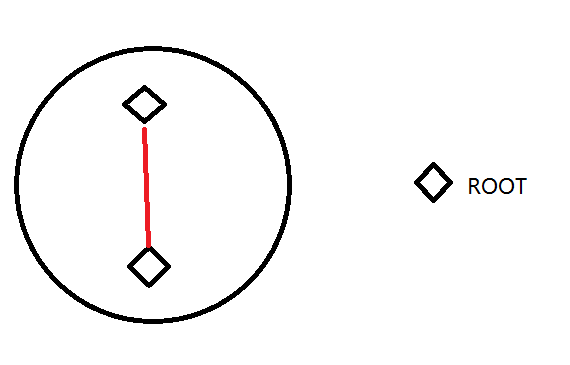
然后分治处理。
这里要注意,分治的时候要求重心, 因为重心可以保证logn的复杂度。不然会被链卡住。
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <string>
using namespace std;
const int INF = 0x3f3f3f3f;
const int maxn = 10010;
int n,k;
int size[maxn];
bool vis[maxn];
struct node{
int to,next,w;
}edge[maxn*2];
int tot,head[maxn];
void init(){
tot = 0; memset(head, -1, sizeof(head));
}
void add_edge(int u, int v, int w){
edge[tot].to = v; edge[tot].w = w;
edge[tot].next = head[u]; head[u] = tot++;
}
int getsize(int u, int pre){
size[u] = 1;
for(int i=head[u]; ~i; i=edge[i].next){
int v = edge[i].to;
if(v == pre || vis[v])continue;
size[u] += getsize(v, u);
}
return size[u];
}
int minn;
void getroot(int u, int pre, int totnum, int &root){
int maxx = totnum - size[u];
for(int i=head[u]; ~i; i=edge[i].next){
int v = edge[i].to;
if(pre == v || vis[v] ) continue;
getroot(v, u, totnum, root);
maxx = max(maxx, size[v]);
}
if(maxx < minn){minn = maxx, root = u;}
}
int dep[maxn];
int st,ed;
void getdepth(int u, int pre, int d){
dep[st++] = d;
for(int i=head[u]; ~i; i=edge[i].next){
int v = edge[i].to;
if(v == pre||vis[v]) continue;
getdepth(v, u, d+edge[i].w);
}
}
int getdep(int a, int b){
sort(dep+a, dep+b);
int ret = 0, e = b-1;
for(int i=a; i<b; i++){
if(dep[i] > k) break;
while( e >= a && dep[e] + dep[i] > k) e--;
ret += e - a + 1;
if( e >= i) ret--;
}
return ret>>1;
}
int solve(int u){
int totnum = getsize(u, -1);
int root, ret = 0;
minn = INF;
getroot(u, -1, totnum, root);
vis[root] = true;
for(int i=head[root]; ~i; i=edge[i].next){
int v = edge[i].to;
if(vis[v]) continue;
ret += solve(v);
}
st = ed = 0;
for(int i=head[root]; ~i; i=edge[i].next){
int v = edge[i].to;
if(vis[v]) continue;
getdepth(v, root, edge[i].w);
ret -= getdep(ed, st);
ed = st;
}
ret += getdep(0, ed);
for(int i=0; i<ed; i++){
if(dep[i] <= k) ret++;
else break;
}
vis[root] = false;
return ret;
}
int main(){
int u,v,w;
while(scanf("%d %d", &n, &k) != EOF&& n+k){
init();
for(int i=1; i<n; i++){
scanf("%d %d %d", &u, &v, &w);
add_edge(u, v, w);
add_edge(v, u, w);
}
memset(vis, false, sizeof(vis));
printf("%d\n", solve(1));
}
}





















 386
386

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








