洛谷 [P3806] 点分治1 (点分治模板)

Link

https://www.luogu.org/problemnew/show/P3806

Description

 给定一棵有$n$个点的树，询问树上距离为$k$的点对是否存在。

Solution

 这是一道点分治的模板题。

 点分治一般有以下几种用法:

• 求路径长度等于或小于等于$k$的点对(路径条数);
• 路径长度为$k$的倍数;
• 路径长度为$k$且路径的边数最少;
• 路径长度对某个数$x$取余后等于$k$;
• 路径上经过的点的个数不能超过$k$，且路径长度最大。

 对于树上的路径来说，可以分为两种：

1. 经过根$root$;
2. 包含于$root$的某一棵子树中，即不经过$root$。

 那么对于第2种可以根据分治思想，将每一棵子树作为子问题，递归处理。对于第1种情况，我们可以从根节点$root$，分成$x-root$以及$root-y$两部分，我们用数组$d$表述子节点到根节点$root$的距离，我们需要求的则是$d[x]+d[y]==k$，且$x$与$y$不在同一棵树内，映射到整棵树，则是对于任意一棵子树来说，找出所有满足上述条件的点对，这即是它的思想。

 那么它是怎么实现的呢，首先考虑到平衡的问题(即子树退化为链的情况)，每次递归计算子树的时候都需要计算一次树的重心，以重心作为子树的根，然后计算。

 对于这棵树的某个子树来说(下文说的树都是它这个子树以及它的子树)，首先计算该树内所有点的$d$值。对于$x$与$y$，直接找它的不同子树的$x$与$y$是很复杂的，（枚举，暴力？)。我们可以这样做，计算出这个树里所有满足$d[x]+d[y]==k$的点对数$cnt1$，这个结果包括$x$与$y$在或者不在同一棵子树的所有情况，我们然后计算出它的所有子树里满足$d[x]+d[y]==k$的点对数$cnt2$，然后$cnt1-cnt2$就是我们需要的结果，在这个过程种可以用递归实现。

 以上仅代表个人浅显见解，仅供个人理解。这里放上一篇写的很好的博客。
https://blog.csdn.net/qq_39553725/article/details/77542223

About

 在记录满足$d[x]+d[y]==k$的点对数时，考虑到树的边取值达到$1e7$，于是想用$map$，以$map[d[x]+d[y]]$的方式记录，然而TLE了，于是改用$unordede{d}_{m}ap$，还是T，最后该用$1e8$的数组才过。

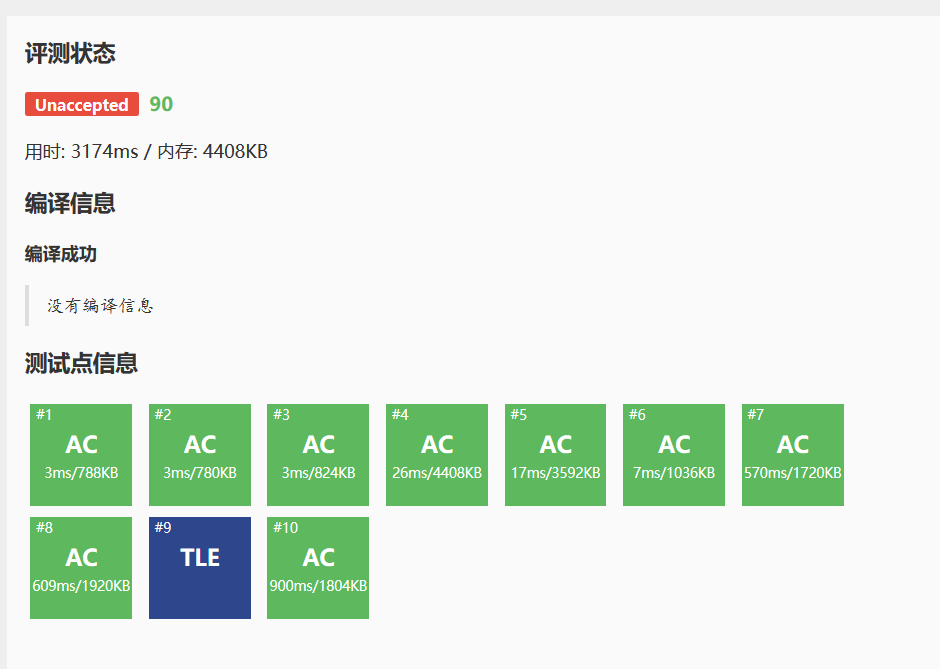
 依次是$map$、$unordered\_map$、数组实现的。

Code

#include<iostream>
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#include<unordered_map>
using namespace std;
#define maxn 10090
#define inf 0x3f3f3f3f
typedef long long ll;
struct edge{
    int u,v,next,w; 
}e[2*maxn];
int head[maxn],cnt;
void add(int x,int y,int w){
    e[cnt].u=x;
    e[cnt].v=y;
    e[cnt].w=w;
    e[cnt].next=head[x];
    head[x]=cnt++;
    e[cnt].u=y;
    e[cnt].v=x;
    e[cnt].w=w;
    e[cnt].next=head[y];
    head[y]=cnt++;
}
int read(){
    int x=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=x*10+c-'0';
        c=getchar();
    }
    return x*f;
}
int S,cot,ans,res,n,m,k,root,sz[maxn],vis[maxn];
int  dis[maxn];
int mp[10000001];
//unordered_map<int,int>mp;
inline void getroot(int x,int fa){
    int maxsz=-1;
    sz[x]=1;
    for(int i=head[x];i!=-1;i=e[i].next){
        int v=e[i].v;
        if(vis[v]||v==fa)continue;
        getroot(v,x);
        sz[x]+=sz[v];
        maxsz=max(sz[v],maxsz);
    }
    maxsz=max(maxsz,S-sz[x]);
    if(res>maxsz)res=maxsz,root=x;
}
inline void getdis(int x,int fa,int len){
    dis[++cot]=len;
    for(int i=head[x];i!=-1;i=e[i].next){
        int v=e[i].v,w=e[i].w;
        if(vis[v]||v==fa)continue;
        getdis(v,x,len+w);
    }
}
inline void cal(int x,int len,int t){
    cot=0;
    getdis(x,0,len);
    for(int i=1;i<=cot;i++)
        for(int j=1;j<i;j++)
            mp[dis[i]+dis[j]]+=t;
}
inline void divide(int x){
    cal(x,0,1);
    vis[x]=1;
    for(int i=head[x];i!=-1;i=e[i].next){
        int v=e[i].v,w=e[i].w;
        if(vis[v])continue;
        cal(v,w,-1);
        S=sz[v],cot=0,res=inf;
        getroot(v,x);
        divide(root);
    }
}
inline void solve(){
    S=n,res=inf;
    getroot(1,0);
    divide(root);
}
int main(){
    n=read(),m=read();
    memset(head,-1,sizeof(head));
    int a,b,c;
    for(int i=0;i<n-1;i++){
        a=read(),b=read(),c=read();
        add(a,b,c);
    }
    solve();
    for(int i=0;i<m;i++){
        k=read();
        if(mp[k])printf("AYE\n");
        else printf("NAY\n");
    }
    return 0;
}

我们坚持一件事情，并不是因为这样做了会有效果，而是坚信，这样做是对的。
——哈维尔