SVM模型有两个非常重要的参数C与gamma。其中 C是惩罚系数,即对误差的宽容度。c越高,说明越不能容忍出现误差,容易过拟合。C越小,容易欠拟合。C过大或过小,泛化能力变差
gamma是选择RBF函数作为kernel后,该函数自带的一个参数。隐含地决定了数据映射到新的特征空间后的分布,gamma越大,支持向量越少,gamma值越小,支持向量越多。支持向量的个数影响训练与预测的速度。
此外大家注意RBF公式里面的sigma和gamma的关系如下:
这里面大家需要注意的就是gamma的物理意义,大家提到很多的RBF的幅宽,它会影响每个支持向量对应的高斯的作用范围,从而影响泛化性能。我的理解:如果gamma设的太大,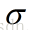
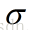
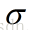
此外,可以明确的两个结论是:
结论1:样本数目少于特征维度并不一定会导致过拟合,这可以参考余凯老师的这句评论:
“这不是原因啊,呵呵。用RBF kernel, 系统的dimension实际上不超过样本数,与特征维数没有一个trivial的关系。”
结论2:RBF核应该可以得到与线性核相近的效果(按照理论,RBF核可以模拟线性核),可能好于线性核,也可能差于,但是,不应该相差太多。
当然,很多问题中,比如维度过高,或者样本海量的情况下,大家更倾向于用线性核,因为效果相当,但是在速度和模型大小方面,线性核会有更好的表现。
老师木还有一句评论,可以加深初学者对SVM的理解:
“须知rbf实际是记忆了若干样例,在sv中各维权重重要性等同。线性核学出的权重是feature weighting作用或特征选择 。”
以上摘录了:http://blog.sina.com.cn/s/blog_6ae183910101cxbv.html
Grid Search
Grid Search是用在Libsvm中的参数搜索方法。很容易理解:就是在C,gamma组成的二维参数矩阵中,依次实验每一对参数的效果。
使用grid Search虽然比较简单,而且看起来很naïve。但是他确实有两个优点:
- 可以得到全局最优
- (C,gamma)相互独立,便于并行化进行








 本文深入解析SVM模型中的C与gamma参数的重要性及其对泛化能力的影响,同时介绍GridSearch方法在参数搜索中的应用。通过实例探讨不同参数设置下模型的性能变化,强调参数选择对模型准确率的影响。
本文深入解析SVM模型中的C与gamma参数的重要性及其对泛化能力的影响,同时介绍GridSearch方法在参数搜索中的应用。通过实例探讨不同参数设置下模型的性能变化,强调参数选择对模型准确率的影响。
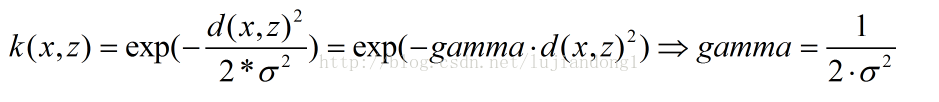
















 3140
3140

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








