【算法设计与分析】分治-第一部分

分治算法

分解：将规模比较大的问题分解成多个子问题，子问题与原问题类似，但是规模更小。
解决：递归继续分解子问题，直至子问题规模达到了直接计算的程度，此时直接得到子问题的解。
合并：根据递归关系，将子问题的解进行合并，求解原问题的解。

二分搜索 Binary Search

输入：一个已排序的数组a[1…n] (元素各不相同)，一个元素x
输出：如果x = a[j]，则返回j，否则返回-1
类似题目：LeetCode-二分查找

顺序搜索：

int sequential_search(const vector<int>& a, int x){
    for(int i=0;i<a.size();i++){
        if(x==a[i]) return i;
    }
    return -1;
}

二分搜索：

分解：将数组分成三部分，数组Left，中间元素a[mid]，数组Right
解决：如果a[mid] = x，则直接返回mid，否则递归继续搜索Left或者Right数组，直到数组为空，则结束搜索。

int binary_search(const vector<int>& a, int x, int l, int h){
    if(l>h) return -1;
    int mid = (l+h)/2;
    if(a[mid]==x) return mid;
    else if(a[mid]>x) return binary_search(a,x,l,mid-1);
    return binary_search(a,x,mid+1,h);
}

时间复杂度分析

顺序搜索：$T(n)=O(n)$

二分搜索：$T(n)=T(n/2)+O(1)$ —> $T(n)=O(logn)$

正确性分析

数组长度：$n=high-low+1$
基本情况：n == 0，此时数组是空的，返回-1。
归纳假设：假设对所有长度小于 的 的⼦数组，命题正确
归纳步骤：证明对长度为k>1的数组，命题正确

• a[mid] == x：算法返回mid ，正确。
• a[mid] < x：因为a有序，所以x在a[mid+1 … high]中，根据归纳假设，⼦
  问题能够正确求解，所以命题正确。
• a[mid] > x：因为a有序，所以x在a[low … mid-1]中，根据归纳假设，⼦
  问题能够正确求解，所以命题正确。

计数 Counting Occurrences

输入：一个已排序的数组a[1…n] (元素各不相同)，一个元素x
输出：元素x出现的次数

遍历计数

从头遍历整个数组，遇到a[i] == x，则计数+1。

int sequential_count(const vector<int>& a, int x){
    int ans=0;
    for(const int& n : a){
        ans+=n==x?1:0;
    }
    return ans;
}

优化的二分搜索计数

普通的二分搜索只能找到相等的某个元素的位置。计数的话，需要根据查找到的下标向左向右遍历比对。

优化二分搜索：先搜索x在数组中的左边界l，如果存在则继续搜索右边界r，如果不存在则说明数组中不存在x。

int binary_count_left(const vector<int>& a, int x, int l, int h){
    if(l>h) return -1;
    int mid=(l+h)/2;
    if((a[mid]==x&&mid==l)||(a[mid]==x&&a[mid-1]<x)) return mid;
    else if((a[mid]==x&&a[mid-1]==x)||a[mid]>x) return binary_count_left(a,x,l,mid-1);
    else  return binary_count_left(a,x,mid+1,h);
}
int binary_count_right(const vector<int>& a, int x, int l, int h){
    if(l>h) return -1;
    int mid=(l+h)/2;
    if((a[mid]==x&&mid==h)||(a[mid]==x&&a[mid+1]>x)) return mid;
    else if((a[mid]==x&&a[mid+1]==x)||a[mid]<x) return binary_count_right(a,x,mid+1,h);
    else  return binary_count_left(a,x,l,mid-1);
}
int binary_count(const vector<int>& a, int x){
    int l = binary_count_left(a, x, 0, a.size()-1);
    if(l==-1) return -1;
    int r = binary_count_right(a, x, 0, a.size()-1);
    cout<<l<<","<<r<<endl;
  

利用C++中的lower_bound和upper_bound函数的实现：

lower_bound(begin(), end(), value) ：在有序容器中查找第一个不小于 value 的元素位置
upper_bound(begin(), end(), value) ：在有序容器中查找第一个大于 value 的元素位置

int binary_count(const vector<int>& a, int x){
    int l = lower_bound(a.begin(), a.end(), x) - a.begin();
    if(l==-1) return -1;
    int r = upper_bound(a.begin(), a.end(), x) - a.begin();
    cout<<l<<","<<r<<endl;
    return r-l;
}

思考题：任务调度

输入：给你 k 个任务和 n 台机器，其中机器 处理⼀个任务所需的时间为
输出：求处理所有任务所需的最短时间

例子： , k = 8 , n = 3, machines = {2, 3, 7}

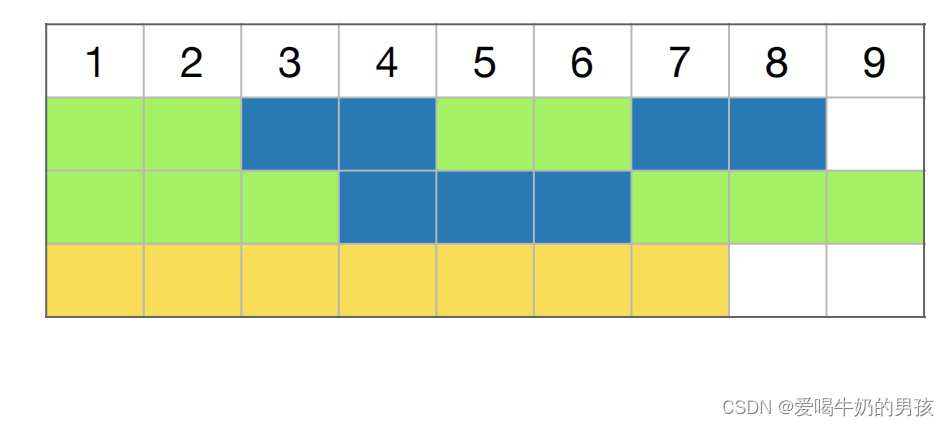
二分方法的任务调度

思路：
寻找一个时间上限(处理一个任务时间最短的机器处理所有k个任务：$k\ast n_{min}$)，对时间进行二分搜索。
对 ${\sum }_{i=1}^n{t}_{mid}/machine{s}_i$ 和 $k$ 进行比较。若前者更大，则说明$t_{mid}$时间下n个机器可以执行更多的任务，往时间更小的区域进行搜索，否则往时间更大搜索。
若${\sum }_{i=1}^n{t}_{mid}/machine{s}_i$ 和 $k$相等，则往左搜索，但包含$t_{mid}$。

代码：

int count_time(vector<int>& machines, int t){
    int ans=0;
    for(const int& machine : machines){
        ans+=(t/machine);
    }
    return ans;
}

int binary_search_for_task_scheduling(vector<int>& machines, int k, int l, int h){
    if(l==h) return l;
    int mid=(l+h)/2, tasks=count_time(machines,mid);
    if(tasks>k) return binary_search_for_task_scheduling(machines,k,l,mid-1);
    else if(tasks==k) return binary_search_for_task_scheduling(machines,k,l,mid);
    return binary_search_for_task_scheduling(machines,k,mid+1,h);
}

时间复杂度：

$$\begin{gathered} T(n)=T(k/2)+O(n) \\ T(n)=O(nlogk) \end{gathered}$$

贪心方法的任务调度

思路：
对每一个机器进行任务分配，先分配给当前花销最小的机器任务(花销是指，机器执行下一个任务的结束时间)，直至所有任务都执行完成。
贪心流程如下：
首先$M_1$执行下一个任务的花销最小，为2，因此将第一个任务分配给$M_1$。

$M_1$的分配任务后，花销变为4，此时花销最小的是$M_2$，分配第二个任务给$M_2$。

$M_2$的分配任务后，花销变为6，此时花销最小的是$M_1$，分配第三个任务给$M_1$。

$M_1$的分配任务后，花销变为6，此时花销最小的共有$M_1$、$M_2$两个机器，选择编号更小的，分配第四个任务给$M_1$。

$M_1$的分配任务后，花销变为8，此时花销最小的是$M_2$，分配第五个任务给$M_2$。

$M_2$的分配任务后，花销变为9，此时花销最小的是$M_3$，分配第六个任务给$M_3$。

$M_3$的分配任务后，花销变为14，此时花销最小的是$M_1$，分配第七个任务给$M_1$。

$M_1$的分配任务后，花销变为10，此时花销最小的是$M_2$，分配第八个任务给$M_2$。

任务分配完毕，此时记录最大的 花销 - 机器一个任务的执行时间。
10-2=8，12-3=9，14-7=7。最大值为9。

代码：

int count_time(vector<int>& times){
    int ans=times[0], index=0;
    for(int i=1;i<times.size();i++){
        index=ans>times[i]?i:index;
    }
    return index;
}

int greedy_for_task_scheduling(vector<int>& machines, int k){
    vector<int> times(machines);
    while(k--){
        int i = count_time(times);
        times[i]+=machines[i];
    }
    int ans=times[0]-machines[0];
    for(int i=1;i<machines.size();i++){
        ans=max(times[i]-machines[i],ans);
    }
    return ans;
}

时间复杂度

$$T(n)=O(k\ast n)$$
对于查找花销最小的函数count_time()，可以尝试构建堆(Heap)或者二叉搜索树(Binary Search Tree)。
优化后的时间复杂度：
$$T(n)=O(n+klogn)$$

数组实现小根堆

// 一般是删除了堆顶元素元素之后，对堆的维护
// 一般删除了堆顶元素，会将堆底的元素移到堆顶，逐层对比将元素进行下沉，直至满足堆的性质
void down_heap(vector<int>& machines, vector<int>& times, int n, int i) {
    if(i>=n) return;
    int smallest = i;
    int left = 2*i+1;
    int right = 2*i+2;
    if (left<n&&times[left]<times[smallest]){
        smallest = left;
    }
    if (right<n &&times[right]<times[smallest]){
        smallest = right;
    }
    if (smallest!=i){
        swap(times[i], times[smallest]);
        swap(machines[i], machines[smallest]);
        down_heap(machines,times, n, smallest);
    }
}

// 一般用于在堆底插入了新元素之后，对于堆的维护
// 原来的堆是符合要求的，只需要将新插入的元素进行调整，放到适当的位置即可
void up_heap(vector<int>& machines, vector<int>& times, int n, int i){
    if(i<0) return;
    int parent = (i-1)/2;
    if (times[parent]>times[i]){
        swap(times[i], times[parent]);
        swap(machines[i], machines[parent]);
        up_heap(machines,times, n, parent);
    }
}

void buildHeap(vector<int>& machines, vector<int>& times){
    int n = machines.size();
    // 从最后一个非叶子节点开始向上构建堆
    for (int i=n/2-1;i>=0;i--) {
        down_heap(machines, times, n, i);
    }
}

int main() {
    vector<int> machines = {2, 3, 7};
    vector<int> times(machines);
    int n = machines.size();
    // 构建小根堆
    buildHeap(machines, times);
    int k=8,ans;
    while(k--){
        times[0]+=machines[0];
        ans=times[0]-machines[0];
        down_heap(machines, times, n, 0);
    }
    cout<<ans<<endl;
    return 0;
}

优先队列实现小根堆

int main() {
    vector<int> machines = {2, 3, 7};
    int n = machines.size();
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> minHeap;
    for(const int& machine : machines){
        minHeap.emplace(make_pair(machine, machine));
    }
    int k=8,ans;
    while(k--){
        auto m = minHeap.top();
        minHeap.pop();
        ans=m.first;
        m.first+=m.second;
        minHeap.emplace(m);
    }
    cout<<ans<<endl;
    return 0;
}

选择 Selection

输入：数组 a[1…n]
输出：数组 a[1]、a[2]、… a[n]的中位数

该问题可以转变的更灵活，寻找数组中第 k 小的数。
类似题目 P1138 第 k 小整数，不过该题需要对数据进行去重。

基于排序算法的选择

将数组 a 先进行排序，然后返回对应的值：

int select(vector<int>& nums, int k){
    sort(nums.begin(), nums.end());
    return nums[k];
}

主要的时间花销为排序的花销：$O(nlogn)$

递归：基于快速排序的选择

快速排序：选择主元。将主元与其他所有的数进行对比，小的放主元左侧，大的放主元右侧。此时主元在数组中的顺序是确定的，再分别对左右两边的数组进行递归排序。

我们可以利用快速排序中，主元与其他元素对比后，左右两边的数的数量来进行选择：
L：小于 等于V 的元素；R：⼤于 V 的元素。

• 如果V的位置刚好为k，则直接返回。
• 如果L的数量包含k，则对左侧进行递归
• 如果R的位置包含k，则对右侧进行递归

int quick_sort_select(vector<int>& nums, int k, int l, int h){
    int t=nums[l], left=l, right=h;
    while(left<right){
        while(nums[right]>t&&right>left) right--;
        if(nums[right]<=t&&right>left)
            nums[left++]=nums[right];
        while(nums[left]<=t&&right>left) left++;
        if(nums[left]>t&&right>left)
            nums[right--]=nums[left];
    }
    nums[left]=t;
    if(left==k) return nums[left];
    else if(left<k) return quick_select(nums,k,left+1,h);
    else return quick_select(nums,k,l,left-1);
}

在 P1138 第 k 小整数中提交的代码：

#include<bits/stdc++.h>
using namespace std;

int quick_select(vector<int>& nums, int k, int l, int h){
    int t=nums[l], left=l, right=h;
    while(left<right){
        while(nums[right]>t&&right>left) right--;
        if(nums[right]<=t&&right>left)
            nums[left++]=nums[right];
        while(nums[left]<=t&&right>left) left++;
        if(nums[left]>t&&right>left)
            nums[right--]=nums[left];
    }
    nums[left]=t;
    if(left==k) return nums[left];
    else if(left<k) return quick_select(nums,k,left+1,h);
    else return quick_select(nums,k,l,left-1);
}

int main(){
    vector<int> nums;
    int n,k,t;
    cin>>n>>k;
    while(n--){
        cin>>t;
        auto it = find(nums.begin(), nums.end(), t);
        if(it == nums.end()){
            nums.push_back(t);
        }
    }
    if(k<=nums.size()) cout<<quick_select(nums, k-1, 0, nums.size()-1)<<endl;
    else cout<<"NO RESULT"<<endl;
    return 0;
}

时间复杂度分析

基于快排的选择，对于根据主元的划分，时间复杂度是：$O(n)$。
如果主元选择的好，使L.length == R.length，那整体的时间复杂度：
$$\begin{gathered} T(n)=T(n/2)+O(n) \\ T(n)=O(nlogn) \end{gathered}$$

但是在我的代码中，默认选择的是第一个。如果 a[] 为升序数组，且要找的是最大值。每一次递归都只会减少一个元素。则最终时间复杂度则会退化为 $O(n)$，和快排本身类似。主元随机的话，也比较看运气。

最坏情况为线性时间的选择算法

优化思路：找到⼀个合适的主元，使得 L 和 R 中⼀定某一个小于等于 7n/10，使得每次的搜索范围最多是上一次的70%。
时间复杂度如下：
$$\begin{gathered} T(n)<=T(7n/10)+T(2n/10)+O(n) \\ T(n)=\Theta (n) \end{gathered}$$

最主要的优化方式：优化寻找主元的方式。
将n个元素分成 ⌊n/5⌋ 组，每组5个元素。最后可能会剩下一些元素无法构成一组。

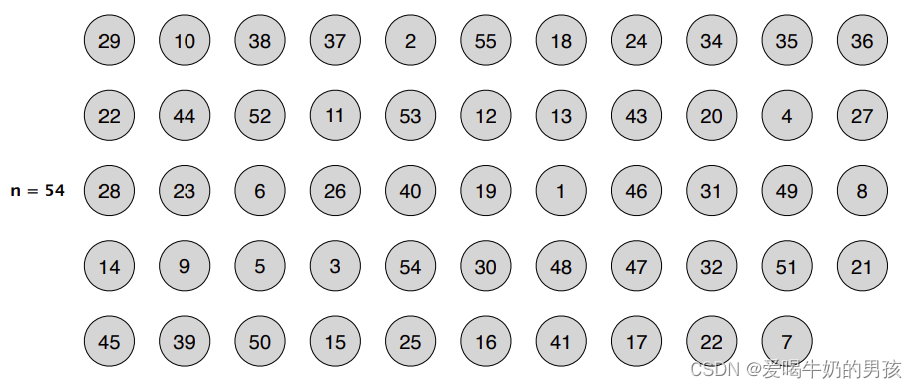
直接计算每一组的中位数（不足5个元素的组除外）

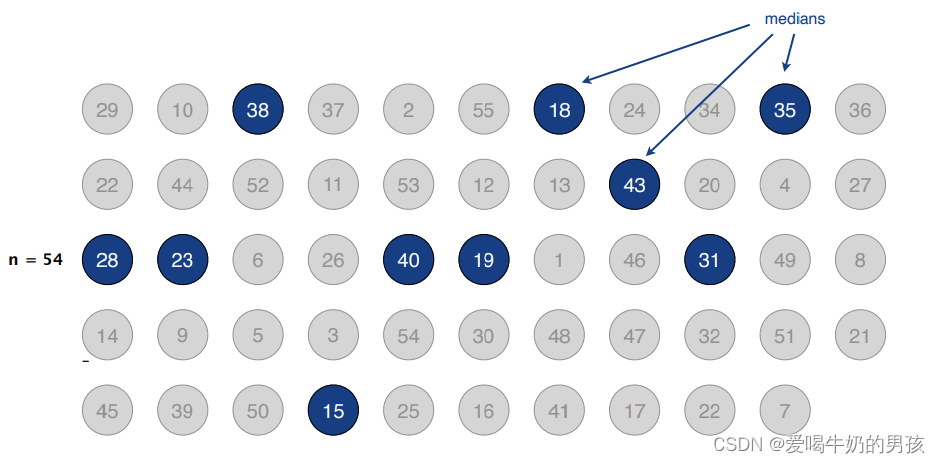
然后将这些这些组的中位数组成一个序列，共 ⌊n/5⌋ 个中位数，寻找他们的中位数：

将寻找到的中位数作为主元。

至少有一半的中位数要小于该主元，因此至少有 ⌊⌊n/5⌋/2⌋ = ⌊n/10⌋ 个中位数小于或等于主元，最终至少有3⌊n/10⌋ 个元素小于等于主元。


至少有一半的中位数要大于该主元，因此至少有 ⌊⌊n/5⌋/2⌋ = ⌊n/10⌋ 个中位数大于或等于主元，最终至少有3⌊n/10⌋ 个元素大于等于主元。

因此最终可以按照这个选择主元的方法，来使 L 和 R 中⼀定有某一个小于等于 7n/10，最终使该选择算法的时间复杂度稳定在线形时间。

#include<bits/stdc++.h>
using namespace std;
//待补充代码
int main(){
	cout<<"待补充代码"<<endl;
}

最近点对 Closest Pair

输入：二维平面上的 n 个点
输出：其中距离最近的两个点

类似题目：P1429 平面最近点对（加强版）

穷举法

枚举可能的所有点对，计算其距离，不断维护最小距离。

时间复杂度

需要枚举所有可能的点对，因此时间复杂度：$O(n^2)$

分治

分解：按照x坐标，选取某个L值，将所有的点均分成两份
解决：递归地求解每侧的最近点对
合并：找到最近的特殊点对，即⼀个点在 的左侧，另⼀个点在 的右侧
返回三者中的最近点对

对于L左右两边的点，我们可以采取不断地分治来计算，然后找到其中每一部分的最近点对，再进行合并。对于分治，我们将点的数目为7定为基本情况，此时可以直接枚举来计算。

对于合并：
假设左侧的最近点对的距离是a1， 右侧的最近点对的距离是a2，令a=min(a1,a2)
仅仅需要考虑距离小于 a 的点。

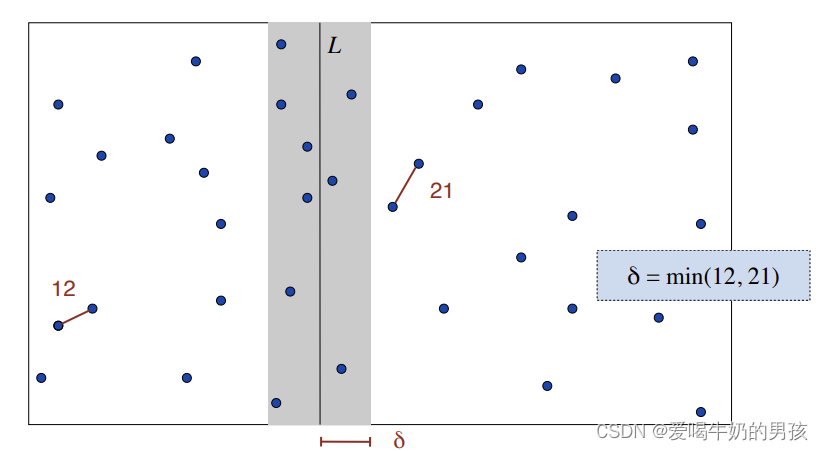
将宽为 2a 的带状区域内的点根据 y 坐标从小到大排序
对于每个点，只需计算它与7个点之间的距离
7n次计算就可以找到特殊的最近点对

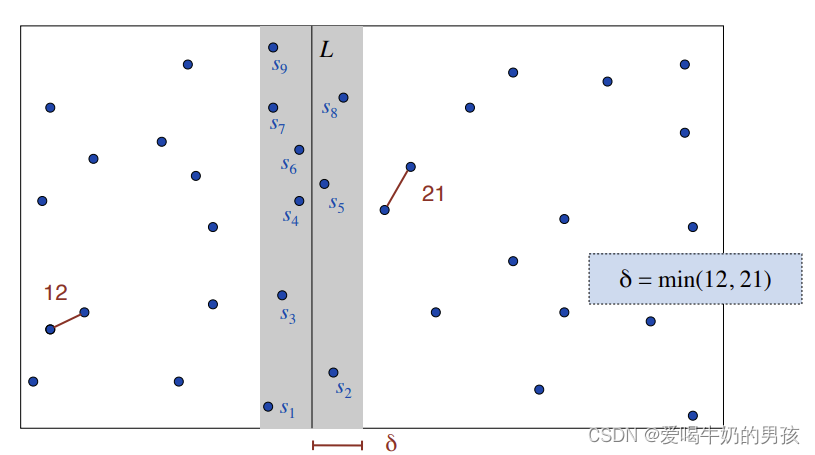
证明：
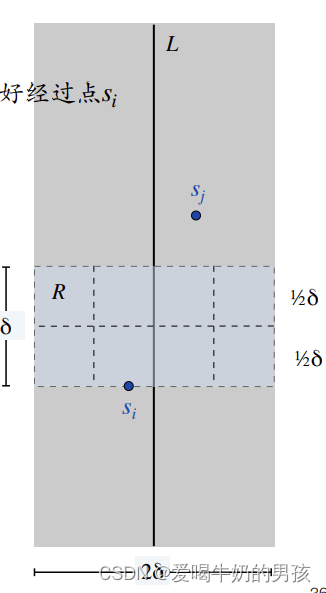
取横跨 L 的 $2\delta$区域中，高为 $\delta$ 的区域，该区域面积为 $\delta \ast 2\delta$。将其划分成八个小正方形，该正方形的对角线长度为 $\delta /\sqrt{2}<\delta$。
假设$S_i$位于该区域的最底部，为满足左部分点对和右部分点对的最近点对距离最小值为$\delta$，因此该区域中只能再存在至多7个点。
如果存在八个点，则说明在L左边或者右边存在一对点，他们的距离要小于$\delta$，和前面得到的左右部分的最近点对的距离不符。

时间复杂度

分割成左右两部分：$O(n)$
分治：$2T(n/2)$
合并时，对于横跨L，且在左右两部分最近点对距离内的点需要进行排序：$O(nlogn)$
$$\begin{gathered} T(n)=2T(n/2)+O(n)+O(nlogn) \\ T(n)=O(nlo{g}^{2}n) \end{gathered}$$

如果我们构造有序的输出，那么就能优化掉合并时候的排序的花销：
输入：
$P_x$：n个点，按照横坐标排序
$P_y$：n个点，按照纵坐标排序
划分：
将n个点划分成L和R两部分
中间变量：
$L_x$：L中的点，按照横坐标排序
$L_y$：L中的点，按照纵坐标排序
$R_x$：R中的点，按照横坐标排序
$R_y$：R中的点，按照纵坐标排序
$A_y$：与垂线距离小于$\delta$的点，按照纵坐标排序

最终时间复杂度：
将n个点按照横纵坐标分成$L_x$、$L_y$、$R_x$、$R_y$：$O(n)$
分治：$2T(n/2)$
得到由$P_y$得到$A_y$：$O(n)$
$$\begin{gathered} T(n)=2T(n/2)+O(n) \\ T(n)=O(nlogn) \end{gathered}$$

代码：

#include <iostream>
#include <complex>
#include <vector>
#include <utility>
#include <math.h>
#include <algorithm>
#include <stdio.h>
#include <chrono>
#include <random>
using namespace std;
typedef long double LD;
typedef complex<LD> Point;
// You can add more functions here.

// 距离的最大值(即用于初始化距离的值)
const LD dbf = sqrt(pow(10000,2) + pow(10000,2));
// 按照x坐标排序的排序规则函数
bool cmp_x(const Point& a, const Point& b){
    if (a.real() == b.real()){
        return a.imag()<b.imag();
    }
    return a.real()<b.real();
}
// 按照y坐标排序的排序规则函数
bool cmp_y(const Point& a, const Point& b){
    if (a.imag() == b.imag()){
        return a.real()<b.real();
    }
    return a.imag()<b.imag();
}
// 计算两个点之间的距离
LD calculate_distance(const Point& a, const Point& b){
    return sqrt(pow(a.real()-b.real(),2) + pow(a.imag()-b.imag(),2));
}
// 用于基本问题的解决，即当问题分到一定的规模就通过此方法直接解决
pair<Point, Point> get_closest_distance(vector<Point>& ay){
    int l=ay.size();
    LD ans=dbf;
    pair<Point, Point> ans_point;
    for(int i=0;i<l;i++){
        for(int j=i+1;j<l;j++){
            LD tmp = calculate_distance(ay[i], ay[j]);
            // cout<<"alex: "<<tmp<<endl;
            if(ans>tmp){
                ans_point.first = ay[i];
                ans_point.second = ay[j];
                ans=tmp;
            }
        }
    }
    return ans_point;
}
// 进行点的二分的函数。
pair<Point, Point> get_closest_pair(vector<Point>& px, vector<Point>& py){
    int l = px.size(); 
    if(l<=7) return get_closest_distance(px);

    int mid = l/2;
    vector<Point> lx(px.begin(), px.begin()+mid);
    vector<Point> rx(px.begin()+mid, px.end());

    vector<Point> ly;
    vector<Point> ry;
    for(auto& p : py){
        // 排序之后，先按照y值进行升序排列，若y值相等，则按照x进行升序排列
        if(p.real()<px[mid].real()||(p.real()==px[mid].real()&&p.imag()<px[mid].imag())){
            ly.emplace_back(p);
        }else{
            ry.emplace_back(p);
        }
    }
    
    // 二分之后往左右两部分子数组，直至子问题满足基本问题的条件
    pair<Point, Point> clo_point_x = get_closest_pair(lx,ly);
    pair<Point, Point> clo_point_y = get_closest_pair(rx,ry);

    pair<Point, Point> ans_point = calculate_distance(clo_point_x.first, clo_point_x.second) < calculate_distance(clo_point_y.first, clo_point_y.second)? clo_point_x : clo_point_y;

    // 获得最小的距离，当前
    LD tmp_clo_dist = calculate_distance(ans_point.first, ans_point.second);


    // 对于横跨二分线的部分点进行最短距离计算
    vector<Point> ay;
    for(auto& p : py){
        if(fabs(p.real()-px[mid].real())<tmp_clo_dist){
            ay.emplace_back(p);
        }
    }

    for(int i=0;i<ay.size();i++){
        for(int j=i+1;j<=ay.size()&&j-i<=7;j++){
            LD tmp = calculate_distance(ay[i], ay[j]);
            if(tmp_clo_dist>tmp){
                ans_point.first = ay[i];
                ans_point.second = ay[j];
                tmp_clo_dist=tmp;
            }
        }
    }
    return ans_point;
}

pair<Point, Point> closest_pair(vector<Point>& P){
    vector<Point> px(P.begin(), P.end());
    vector<Point> py(P.begin(), P.end());
    
    sort(px.begin(), px.end(), cmp_x);
    sort(py.begin(), py.end(), cmp_y);
    return get_closest_pair(px, py);
}

// 自动生成浮点数函数
vector<Point> generate_points(int n){
    random_device rd;
    mt19937 gen(rd());
    LD min_value = -10000;
    LD max_value = 10000;
    uniform_real_distribution<LD> distribution(min_value, max_value);
    vector<Point> points;
    while(n--){
        LD rx = distribution(gen);
        LD ry = distribution(gen);
        points.emplace_back(Point(rx,ry));
    }
    return points;
}


int main(int argc, const char * argv[]) {
    // You can insert code here to test your function.
    int ns[] = {100, 1000, 10000, 100000};
    for(int& n : ns){
        auto start = chrono::high_resolution_clock::now();
        vector<Point> p=generate_points(n);
        pair<Point, Point> ans = closest_pair(p);
        auto end = chrono::high_resolution_clock::now();
        auto duration = chrono::duration_cast<chrono::microseconds>(end - start);
        cout << "程序执行时间: " << duration.count() << " ms" << endl;
        LD aa = calculate_distance(ans.first, ans.second);
        cout<<"点集的规模: "<<n<<", 最近点对:("<<ans.first.real()<<","<<ans.first.real()<<"), ("<<ans.second.real()<<","<<ans.second.real()<<")"<<endl;
        cout<<"最近点对的距离为"<<aa<<"\n"<<endl;
    } 
    return 0;
}

P1429 平面最近点对（加强版）中提交的代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1000001;
const int INF = 2 << 20;
struct Point{
    double x,y;
}s[maxn], tmp[maxn];

bool cmp_x(const Point& a, const Point& b){
    if (a.x == b.x){
        return a.y<b.y;
    }
    return a.x<b.x;
}

bool cmp_y(const Point& a, const Point& b){
    if (a.y == b.y){
        return a.x<b.x;
    }
    return a.y<b.y;
}

double calculate_distance(const Point& a, const Point& b){
    return sqrt(pow(a.x-b.x,2) + pow(a.y-b.y,2));
}

double merge(int l, int h){
    double ans = INF;
    if(l==h) return ans;
    else if(l+1==h) return calculate_distance(s[l], s[h]);
    int mid = (l+h)/2;
    double d1 = merge(l, mid);
    double d2 = merge(mid+1, h);
    double d = min(d1,d2);
    int k = 0;
    for(int i=l;i<=h;i++){
        if(fabs(s[i].x-s[mid].x)<d){
            tmp[k].x=s[i].x;
            tmp[k].y=s[i].y;
            k++;
        }
    }
    sort(tmp, tmp + k, cmp_y);
    for(int i = 0; i < k; i++){
        for(int j = i + 1; j < k && s[j].y - s[i].y < d; j++) {
            double d3 = calculate_distance(tmp[i], tmp[j]);
            if(d > d3) d = d3;
        }
    }
    return d;
}

int main() {
    // Point a = Point(31.1, 32.2);
    // You can insert code here to test your function.
    int n;cin>>n;
    double x,y;
    for(int i=0;i<n;i++){
        cin>>x>>y;
        s[i].x=x;s[i].y=y;
    }
    sort(s,s+n,cmp_x);
    double aa = merge(0,n-1);
    printf("%.4lf\n",aa);
    return 0;
}

提交结果：