| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 133338 | Accepted: 64845 |
Description
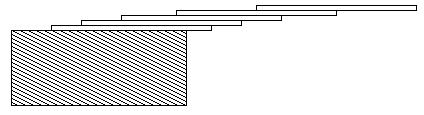
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.
Input
Output
Sample Input
1.00 3.71 0.04 5.19
Sample Output
3 card(s) 61 card(s) 1 card(s)
二分法求解
先离线计算len[i]为前i张卡片向桌子外延伸的长度
二分查找的过程:初始时区间[l,r]=[1,total],区间的中间指针min=(l+r)/2,二分搜索,直到l+1>=r为止。
#include<iostream>
using namespace std;
const int maxn=300;
const double delta=1e-8;
int zero(double x)//如果误差在delta内则返回0
{
if(x<-delta) return -1;
return x>delta;
}
int main()
{
double len[maxn];len[0]=0.0;
int total;
for(total=1;zero(len[total-1]-5.20)<0;total++)//计算出截至长度不超过5.20所需的最少卡片数
len[total]=len[total-1]+1.0/double(total+1);
double x;cin>>x;
while(zero(x))//二分法
{
int l,r;l=0;r=total;//设定查找左右区间
while(l+1<r)//循环条件是查找区间存在
{
int mid=(l+r)/2;//中间指针
if(zero(len[mid]-x)<0) l=mid;//若中间元素值小于x,则在右区间查找,否则则在左区间查找
else r=mid;
}
cout<<r<<" card(s)"<<endl;
cin>>x;
}
return 0;
}






















 5412
5412

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








