几何算法——10.欧拉操作

一只特立独行的蚂蚁

已于 2022-12-17 09:57:27 修改

阅读量2.1k

点赞数

分类专栏：几何算法文章标签：几何学算法

于 2022-11-19 12:36:39 首次发布

本文链接：https://blog.csdn.net/luolei188/article/details/127935267

版权

几何算法专栏收录该内容

4 篇文章 12 订阅

订阅专栏

几何算法——10.欧拉操作

1 欧拉操作
2. 非流形体
- 2.1 非流形模型（non-manifold model）
- 2.2 扩展的欧拉公式

1 欧拉操作

欧拉操作，是由 B.G. Baumgart 于1972年提出，目的是提供有效、正确地建立三维物体复杂的边界数据结构的方法（保证有效性、保证通用性）。

1.1 欧拉操作的设计思想

（1）提供少数几个公用的边界数据结构生成操作，使得三维物体复杂的边界数据结构可通过这些公用操作逐步构造完成。
（2）基于欧拉公式保证使用公用数据结构生成操作所生成的边界数据结构具有拓扑有效性。

欧拉公式： v(点数)－e(边数) + f(面数) ＝ 2（s(分离体数) – h（通孔数））+ r(内环数)

以一个立方体为例：
在这里插入图片描述
有8个顶点，12条边，6个面，只有1个体，0个通孔，0个内环。

再以一个带孔的立方体为例：
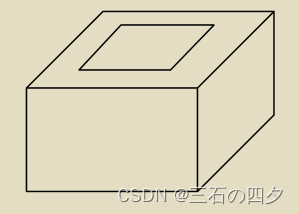
在这里插入图片描述
有16个顶点，24条边，6个面，只有1个体，1个通孔，2个内环。也满足欧拉公式。

对于圆环，可以看作是这个带洞立方体的拓扑同胚，也满足欧拉公式：
如果将绿色当作一条真实的边：2 - 4 + 2 = 2（1 - 1） + 0。
如果绿色不当作真实的边：1 - 2 + 1 = 2 （1 - 1） + 0。
在这里插入图片描述
对于圆柱体，也满足欧拉公式（4 - 6 + 4 = 2 *（1 - 0） + 0）。

1.2 欧拉操作的选取

原则：取具有明显几何意义的基：造点、造边、造环、造面、造体

本文中使用的名称的关键字如下:
在这里插入图片描述
For instance, the name “mev” translates as “Make Edge, vertex”.

C.Braid 所取了一组基：
mvfs，mev，mef，kemr，kfmrh

1.3 几个典型的欧拉操作

对于拓扑的操作分为三大类，若干小类。
三大类是：Skeletal Primitives，Local Manipulations和Global Manipulations。
Skeletal Primitives是指构造一个skeletal plane model，它是从无到有构造更复杂模型的基础，对应拓扑操作就是MVFS。
局部拓扑操作又分为若干小类：在skeletal plane model的基础上，其他的各种不改变亏格的模型都可以在此基础上，通过Local Manipulations生成出来。
全局拓扑操作：由于skeletal plane model是一个亏格为0的模型（如下图9.2，类似立方体，亏格为0，没有洞）。想构造亏格大于0的模型（如下图9.3），如甜甜圈（亏格为1的模型），或者多个甜甜圈粘合在一起的（亏格大于1的模型），就需要Global Manipulations。
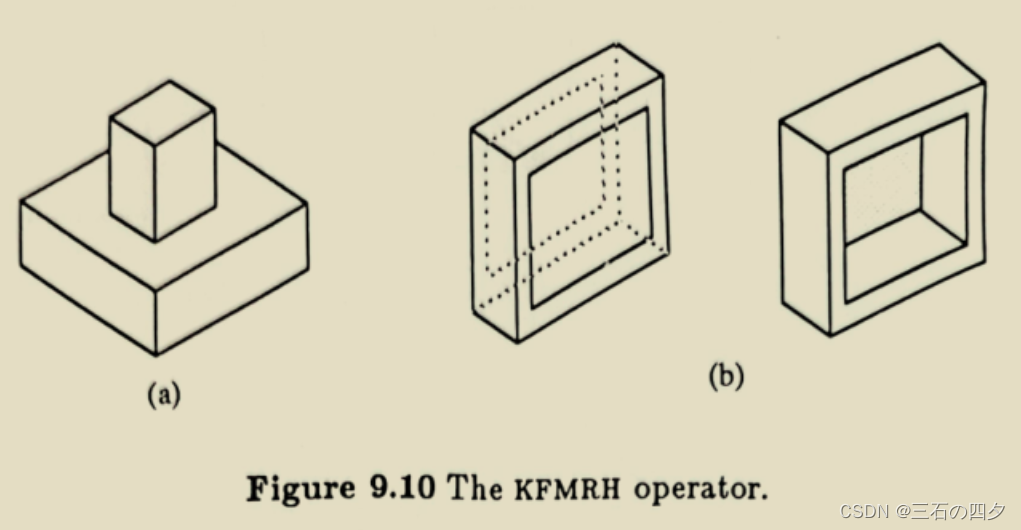
在这里插入图片描述