
之前我们学习的机器学习算法都是属于分类算法,也就是预测值是离散值。当预测值为连续值时,就需要使用回归算法。本文将介绍线性回归的原理和代码实现。
线性回归原理与推导
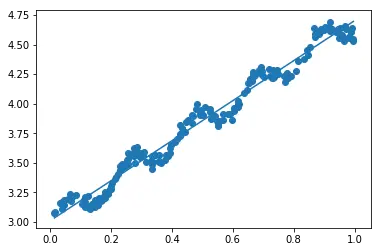
如图所示,这时一组二维的数据,我们先想想如何通过一条直线较好的拟合这些散点了?直白的说:尽量让拟合的直线穿过这些散点(这些点离拟合直线很近)。
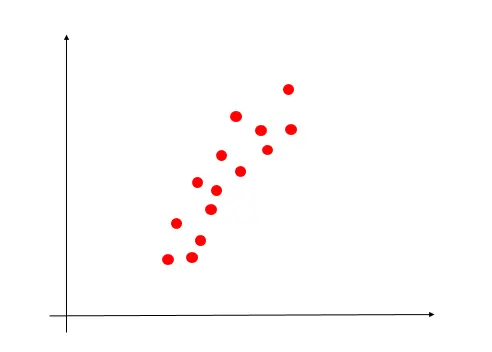
目标函数
要使这些点离拟合直线很近,我们需要用数学公式来表示。首先,我们要求的直线公式为:Y = XTw。我们这里要求的就是这个w向量(类似于logistic回归)。误差最小,也就是预测值y和真实值的y的差值小,我们这里采用平方误差:
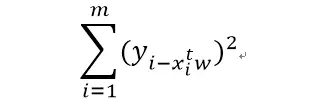
求解
我们所需要做的就是让这个平方误差最小即可,那就对w求导,最后w的计算公式为:
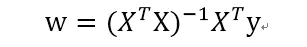
我们称这个方法为OLS,也就是“普通最小二乘法”
线性回归实践
数据情况
我们首先读入数据并用matplotlib库来显示这些数据。
def loadDataSet(filename):
numFeat = len(open(filename).readline().split('\t')) - 1
dataMat = [];labelMat = []
fr = open(filename)
for line in fr.readlines():
lineArr = []
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat, labelMat
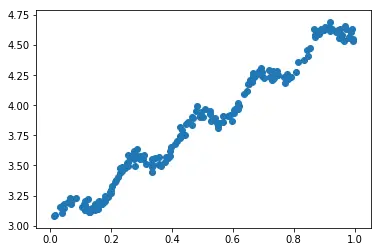
回归算法
这里直接求w就行,然后对直线进行可视化。
def standRegres(Xarr,yarr):
X = mat(Xarr);y = mat(yarr).T
XTX = X.T * X
if linalg.det(XTX) == 0:
print('不能求逆')
return
w = XTX.I * (X.T*y)
return w
算法优缺点
- 优点:易于理解和计算
- 缺点:精度不高





















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








