线性学习中最基础的回归之一,本文从线性回归的数学假设,公式推导,模型算法以及实际代码运行几方面对这一回归进行全面的剖析~
一:线性回归的数学假设
1.假设输入的X和Y是线性关系,预测的y与X通过线性方程建立机器学习模型
2.输入的Y和X之间满足方程Y=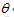
二、线性回归建模
2.1方程式表示:
数学形式:
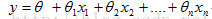
矩阵形式:
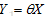
其中,X矩阵是m行(n+1)列的,每一行是一个样本,每一列是样本的某一个特征
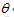 矩阵(n+1)行一列的,它是X的权重,也是线性回归要学习的参数
矩阵(n+1)行一列的,它是X的权重,也是线性回归要学习的参数
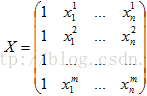
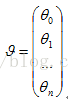
2.2 损失函数(Loss function)
对数极大似然和最小二乘的联系:
由线性函数的假设知道,噪音项满足高斯分布,其中一个样本的正态分布的数学表达为:
那么,通过极大估计求得似然函数为所有样本的乘积,如下:
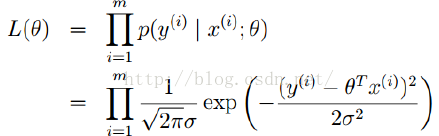
经过数学运算和推导,求极大似然的最大值可以转化为求其log函数的最大值,推导过程如下:








 本文全面解析机器学习中的线性回归,详细阐述了线性回归的数学假设,包括线性关系和误差项的性质。此外,还介绍了线性回归模型的构建过程,并提供了实际代码实现的概述。
本文全面解析机器学习中的线性回归,详细阐述了线性回归的数学假设,包括线性关系和误差项的性质。此外,还介绍了线性回归模型的构建过程,并提供了实际代码实现的概述。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 8583
8583

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








