二叉树各种遍历算法(递归及非递归算法)

最新推荐文章于 2022-06-28 21:54:25 发布
最新推荐文章于 2022-06-28 21:54:25 发布
阅读量713 收藏 1
点赞数
分类专栏： 数据结构与算法 文章标签： ??? ?? ??
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/luoluozlb/article/details/52093013
版权
遍历的概念：

所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。遍历是二叉树上最重要的运算之一，是二叉树上进行其它运算之基础。二叉树上访问结点所做的操作依赖于具体的应用问题。

遍历方式：

根据访问结点操作发生位置命名：

① NLR：前序遍历(PreorderTraversal亦称（先序遍历））

——访问根结点的操作发生在遍历其左右子树之前。

② LNR：中序遍历(InorderTraversal)

——访问根结点的操作发生在遍历其左右子树之中（间）。

③ LRN：后序遍历(PostorderTraversal)

——访问根结点的操作发生在遍历其左右子树之后。

完整的代码（C++）：

#include <iostream>
#include <queue>
#include <stack>
#include <utility>
using namespace std;

/***********************************************************************************/
/********************************* 定义接口 ****************************************/
/***********************************************************************************/

//二叉树节点 
template <typename T>
struct BiTree
{
    T *data;
    BiTree *par, *lChild, *rChild;
};

// 构造一个值为data_value的树节点 
template <typename T> BiTree<T>* CreateBiTree(const T &data_value); 

// 销毁树 
template <typename T> void destory(BiTree<T> *bT);

// 判断树是否为空 
template <typename T> bool empty(BiTree<T> *bT);

// 计算树的深度 
template <typename T> int depth(BiTree<T> *bT);

// 把另外一棵树插入到子树中 
template <typename T>
BiTree<T>* insert(BiTree<T> *bT, BiTree<T> *newBt, const bool &isLeft);

// 生成值为value的新节点插入到子树中 
template <typename T>
BiTree<T>* insert(BiTree<T>* bT, const T &value, const bool &isLeft);

// 获取树的根 
template <typename T> BiTree<T>* root(BiTree<T>* bT);

// 查找值为value的子树
template <typename T> BiTree<T>* find(BiTree<T>* bT, const T &value);

// 三种遍历方式(递归)： 先序、中序、后序 
template <typename T> void beforeOrder_traverse_d(BiTree<T>* bT);
template <typename T> void infixOrder_traverse_d(BiTree<T>* bT);
template <typename T> void afterOrder_traverse_d(BiTree<T>* bT);

// 三种遍历方式(非递归)： 先序、中序、后序 
template <typename T> void beforeOrder_traverse(BiTree<T>* bT);
template <typename T> void infixOrder_traverse(BiTree<T>* bT);
template <typename T> void afterOrder_traverse(BiTree<T>* bT);

//层序遍历 
template <typename T> void layerOrder_traverse(BiTree<T>* bT); 


/***********************************************************************************/
/********************************* 接口实现 ****************************************/
/***********************************************************************************/

template <typename T>
BiTree<T>* CreateBiTree(const T &data_value)
{
    BiTree<T>* bT = new BiTree<T>;
    bT->data = new T(data_value);
    bT->par = bT->lChild = bT->rChild = NULL;
    return bT;
}

template <typename T>
void destory(BiTree<T> *bT)
{
    if(bT){
        destory(bT->lChild);
        destory(bT->rChild);
        delete bT->data;
        delete bT;
    }
}

template <typename T>
bool empty(BiTree<T> *bT)
{
    return bT == NULL;
}

template <typename T>
int depth(BiTree<T> *bT)
{
    if(bT){
        int lDepth = depth(bT->lChild), rDepth = depth(bT->rChild);
        return 1 + (lDepth > rDepth ? lDepth : rDepth);
    }
    else{
        return 0;
    }
}

template <typename T>
BiTree<T>* insert(BiTree<T> *bT, BiTree<T> *newBt, const bool &isLeft)
{
    if(isLeft){
        bT->lChild = newBt;
    }
    else{
        bT->rChild = newBt;
    }
    newBt->par = bT;
    return newBt;
}

template <typename T>
BiTree<T>* insert(BiTree<T>* bT, const T &value, const bool &isLeft)
{
    BiTree<T>* newBt = CreateBiTree(value);
    return insert(bT, newBt, isLeft);
}

template <typename T>
BiTree<T>* root(BiTree<T>* bT)
{
    return bT->par ? root(bT->par) : bT;
}

template <typename T>
BiTree<T>* find(BiTree<T>* bT, const T &value)
{
    if(value == *(bT->data)){
        return bT;
    }

    BiTree<T>* res = NULL;
    if(bT->lChild){
        res = find(bT->lChild, value);
        if(res){
            return res;
        }
    }
    if(bT->rChild){
        res = find(bT->rChild, value);
        if(res){
            return res;
        }
    }

    return res;
}

template <typename T>
void beforeOrder_traverse_d(BiTree<T>* bT)
{
    if(bT){
        cout << *(bT->data) << " ";
        beforeOrder_traverse_d(bT->lChild);
        beforeOrder_traverse_d(bT->rChild);
    }
}

template <typename T>
void infixOrder_traverse_d(BiTree<T>* bT)
{
    if(bT){
        infixOrder_traverse_d(bT->lChild);
        cout << *(bT->data) << " ";
        infixOrder_traverse_d(bT->rChild);
    }
}

template <typename T>
void afterOrder_traverse_d(BiTree<T>* bT)
{
    if(bT){
        afterOrder_traverse_d(bT->lChild);
        afterOrder_traverse_d(bT->rChild);
        cout << *(bT->data) << " ";
    }
}

template <typename T>
void beforeOrder_traverse(BiTree<T>* bT)
{
    stack<BiTree<T>*> st;
    BiTree<T>* t = bT;

    while(t || ! st.empty()){
        if(t){
            cout << *(t->data) << " ";
            st.push(t);
            t = t->lChild;
        }
        else{
            t = st.top();
            st.pop();
            t = t->rChild;
        }
    }
}

template <typename T>
void infixOrder_traverse(BiTree<T>* bT)
{
    stack<BiTree<T>*> st;
    BiTree<T>* t = bT;

    while(t || ! st.empty()){
        if(t){
            st.push(t);
            t = t->lChild;
        }
        else{
            t = st.top();
            st.pop();
            cout << *(t->data) << " ";
            t = t->rChild;
        }
    }
}

template <typename T>
void afterOrder_traverse(BiTree<T>* bT)
{
    stack< pair<char, BiTree<T>*> > st;
    BiTree<T>* t = bT;

    while(t || ! st.empty()){

        // 遍历左子树
        while(t){
            st.push( pair<char, BiTree<T>*>('L', t) );
            t = t->lChild;
        }

        // 左右子树访问完毕访问根节点  
        while(! st.empty() && st.top().first == 'R'){
            cout << *(st.top().second->data) << " ";
            st.pop();
        }

        // 遍历右子树
        if(! st.empty()){
            st.top().first = 'R';
            t = st.top().second;
            t = t->rChild;
        }
    }
}

template <typename T>
void layerOrder_traverse(BiTree<T>* bT)
{
    queue<BiTree<T>*> que;
    que.push(bT);

    while(! que.empty()){
        BiTree<T>* t = que.front();
        if(t){
            cout << *(t->data) << " ";
            que.push(t->lChild);
            que.push(t->rChild);
        }
        que.pop();
    }
}


/***********************************************************************************/
/***********************************************************************************/
/***********************************************************************************/

int main()
{
    BiTree<int>* bT = CreateBiTree(0);

    auto b1 = insert(bT, 1, true);
    insert(bT, 2, false);
    insert(b1, 3, true);
    insert(b1, 4, false);
    auto b2 = find(bT, 2);
    auto rootT = root(insert(b2, 5, true)); 

    cout << "树的深度：" << depth(bT) << endl;

    cout << "先序遍历(递归)：";
    beforeOrder_traverse_d(rootT);
    cout << endl;

    cout << "中序遍历(递归)：";
    infixOrder_traverse_d(rootT);
    cout << endl;

    cout << "后序遍历(递归)：";
    afterOrder_traverse_d(rootT);
    cout << endl;

    cout << "先序遍历(非递归)：";
    beforeOrder_traverse(rootT);
    cout << endl;

    cout << "中序遍历(非递归)：";
    infixOrder_traverse(rootT);
    cout << endl;

    cout << "后序遍历(非递归)：";
    afterOrder_traverse(rootT);
    cout << endl;

    cout << "层序遍历：";
    layerOrder_traverse(bT);
    cout << endl;

    destory(bT);
    return 0;
}

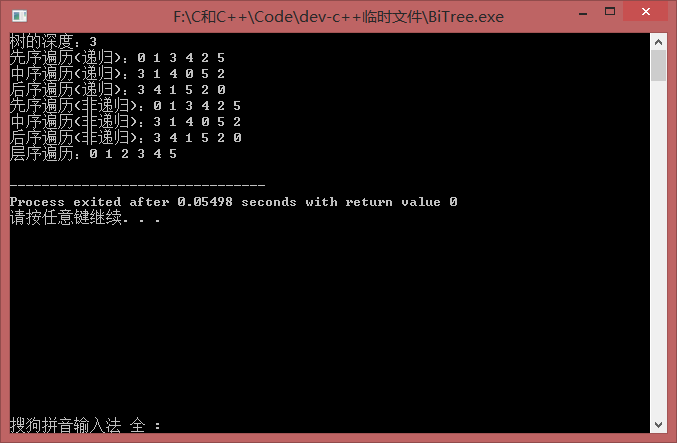
效果图：

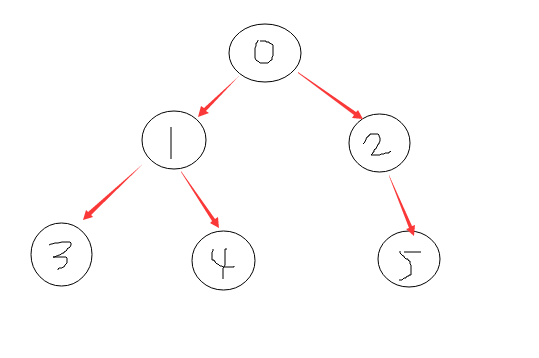
这里写图片描述
（手画的^_^）

这里写图片描述

2018-8-15 编辑添加：

重新学习数据结构时，发现另外一种二叉树后序遍历非递归算法，代码如下：

//后序遍历二叉树 
template <typename T>
void afterOrder_traverse(BiTree<T>* bT)
{
    BiTree<T>* t = bT;
    if(t != NULL) {
        stack<BiTree<T>*> s;
        do {
            //将所有最左结点压栈
            while(t) {
                s.push(t);
                t = t->lChild;
            }

            int flag = true;                     // flag为true表示当前结点的左孩子为空或者已被访问
            BiTree<T>* lastVisit = NULL;         // 上一次访问的节点 

            while(!s.empty() && flag) {
                t = s.top();                     // 注意：这里只是获取栈顶元素，而并没有出栈
                if(t->rChild == lastVisit) {     // 如果当前结点右孩子为空，或者已经被访问过，则访问当前结点
                    s.pop();                     // 当前结点出栈
                    cout << *(t->data) << " ";   // 访问节点 
                    lastVisit = t;               // 指针变量指向当前结点
                } else {                         // 如果当前结点右孩子不为空，则先去处理右孩子
                    t = t->rChild;               // 处理右孩子
                    flag = false;                // t的左孩子未被访问，flag置为false
                    //lastVisit = t;             // 可省略 
                }
            }
        } while(!s.empty());
    }
}
luoluolzb
关注
专栏目录
二叉树遍历——递归与非递归实现
jjy223404的博客
04-27 885
二叉树遍历——递归与非递归实现描述分析递归版本的二叉树遍历设计代码非递归版本的二叉树遍历非递归先序遍历设计步骤代码非递归后序遍历设计步骤代码非递归中序遍历设计步骤代码非递归遍历二叉树完整代码及测试 描述 实现二叉树的先序、中序、后序遍历，包括递归方式和非递归方式。 分析 使用递归实现二叉树遍历十分容易。在递归过程中，系统自动帮你压栈从而回溯时，关键信息不会被丢失。而非递归实现二叉树遍历时，无法再依...
Java二叉树前序遍历：递归+非递归实现，非递归详解
进击的Coder*的博客
04-13 1901
二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。 如下便是一棵二叉树： 二叉树的前序遍历： 1. 遍历根节点 2. 如果存在左子树，先序遍历左子树 3. 如果存在右子树，先序遍历右子树 二叉树结构定义： class TreeNode { int val; TreeNode left; TreeNode right; TreeNode() {} TreeNode(int val) { this.va
二叉树的遍历代码
热门推荐
Big Data
03-18 1万+
https://www.jianshu.com/p/456af5480cee 一、先序遍历 考察到一个节点后，即刻输出该节点的值，并继续遍历其左右子树。(根左右) public static void 先序非递归(TreeNode root) { Stack<TreeNode> stack = new Stack<>(); TreeNode node...
【数据结构】二叉树的非递归遍历（完整代码）
ly_6699的博客
02-23 3072
题目描述 按要求建立一棵树（#表示空），并用非递归的方法对它进行遍历 解题思路 1.递归遍历：则将二叉树的遍历看作是分治问题，将每一棵树都分为根-左子树-右子树三部分，每部分按同样的方法递归遍历即可。具体实现见下篇博客 [二叉树的实现&递归遍历](https://blog.csdn.net/ly_6699/article/details/87891642) 2.非递归遍历：我们可以借用栈的知识完成树的遍历。使用栈完成的过程以下面的前序遍历为例
*二叉树的遍历（递归与非递归方式）
IMUHERO
04-05 329
一、二叉树的遍历 二叉树是一种使用广泛的数据结构，掌握二叉树的遍历方式至关重要，以下列出了二叉树的四种遍历分析，其中前、中、后序遍历分别使用递归和非递归方式来实现。 =>层序遍历、前序遍历、中序遍历、后续遍历 二、前提条件 假设构造部分如下： import java.util.Stack; import java.util.Queue; import java.util.Link...
二叉树的遍历（递归、非递归）
yishizuofei的博客
09-23 994
二叉树遍历的基本概念 1、二叉树遍历原理：二叉树的遍历是指从根结点出发，按照某种次序依次访问所有结点，使得每个结点被访问一次且仅被访问一次。 2、二叉树遍历方法： （1）前序遍历：若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。 （2）中序遍历：若树为空，则空操作返回，否则从根结点开始，中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树。 （
二叉树先序遍历、中序遍历和后序遍历非递归算法 C++源码
08-25
用C++写的二叉树先序遍历、中序遍历和后序遍历非递归算法
二叉树前序遍历的非递归算法
09-04
"二叉树前序遍历的非递归算法" 二叉树前序遍历的非递归算法是指在不使用递归函数的情况下，对二叉树进行前序遍历的算法。前序遍历是指先访问根节点，然后访问左子树，最后访问右子树。 在了解非递归算法之前，我们...
二叉树先序遍历的非递归算法具体实现
12-10
在前面一文，说过二叉树的递归遍历算法（二叉树先根（先序）遍历的改进），此文主要讲二叉树的非递归算法，采用栈结构 总结先根遍历得到的非递归算法思想如下： 1）入栈，主要是先头结点入栈，然后visit此结点 2）...
二叉树非递归遍历算法分析
weixin_43875867的博客
05-08 1137
本文介绍了二叉树非递归遍历算法的一种实现方式，以及这种遍历算法是怎么推导出来的。
二叉树的非递归遍历
10-20
二叉树的非递归遍历，使用C++实现二叉树的非递归遍历，对正在学习算法的同学应该挺有帮助的
二叉树的递归与非递归遍历
weixin_40486179的博客
06-28 181
前中后序遍历顺序如下： 前序遍历（中左右）：5 4 1 2 6 7 8 中序遍历（左中右）：1 4 2 5 7 6 8 后序遍历（左右中）：1 2 4 7 8 6 5
二叉树的遍历的递归与非递归实现
a760352276的博客
10-27 1399
二叉树的遍历问题1.递归序2.递归方法遍历二叉树3.非递归方法遍历前序遍历后序遍历：中序遍历：小结： 1.递归序 抛开二叉树的遍历。我们来单看一个普通的递归函数： public static void DiGui(Tree node){ if(node == null){ return; } /* 节点第一次到达DiGui函数体 */ System.out.println("first time:" + node.val
二叉树的递归和非递归遍历（java）
Aaron
05-25 1174
package com.wy.binarytree; import java.util.LinkedList; import java.util.Queue; import java.util.Stack; public class BinaryTree { private TreeNode root = null; public BinaryTree(){ root = new
二叉树遍历代码
qq_43556545的博客
10-15 291
今天复习了一下二叉树的遍历，当初学数据结构的时候没有好好理解，迭代的代码如下： //前序 vector preorderTraversal(TreeNode* root) { if(!root) return {}; vector result; stack<TreeNode*> stk; stk.push(root); while(!stk.empty()){ TreeNode* node = stk.top(); stk.pop(); if(node){ if(node -> righ
二叉树的遍历（代码）
qing_feng__的博客
11-26 386
#include #include using namespace std; typedef struct BTNode { int data; struct BTNode *lchild,*rchild; } BiTNode,*BiTree; int Create(BiTree &T)//创建树,0表示空树 { int c; scanf("%d",&c); if (c =
遍历二叉树代码
In ShangHai | 分析技术的点点滴滴。
08-03 549
#include #include   //二叉树的的 #define MAXSIZE 100 //二叉树中最多的结点数　 typedef char TElemType;  typedef struct BiTNode{     TElemType data;     struct BiTNode *lchild,*rchild; }BiTNode,*BiTree;  
二叉树的遍历 （代码）
春秋繁露
07-08 549
#include #include #include #include #include #define TRUE 1 #define FALSE 0 #define BEGIN 0 #define ALPHA 1 #define LEFT_BRACKET 2 #define COMMA 3 #define RIGHT_BRACKET 4 #define LEFT_CHI
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值