关于图的介绍网上很多,这里就不介绍了,直接上代码:
最小生成树算法可以看看:http://www.cnblogs.com/biyeymyhjob/archive/2012/07/30/2615542.html
#include <iostream>
#include <iomanip>
#include <climits>
#include <queue>
using namespace std;
#define MAX_VERTEX_NUM 20 // 顶点数量上限
typedef char VerType; // 顶点结构 , 顶点的字母名称
typedef int ArcType; // 边的结构 , 权值
typedef enum {DG, UDG} GKind; // 图类型,{有向图,无向图}
// 图的存储结构
typedef struct
{
int verNum, arcNum; // 顶点数量, 边数量
GKind kind; // 图类型
VerType vertex[MAX_VERTEX_NUM]; //顶点
ArcType arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //边
}Graph;
void CreateGraphByArray(Graph &G); // 创建图G (通过预定义的数组)
void CreateGraph(Graph &G); // 创建图G (通过输入)
int VertexLoc(const Graph &G, const VerType &v); // 获取顶点v在图G中的位置
void PrintGraphArcs(const Graph &G); // 输出图G邻接矩阵
void DFS(const Graph G, int vi, bool visited[]); // 图G的深度优先遍历的准备
void DFS_Traverse(const Graph &G); // 图G的深度优先遍历
void BFS_Traverse(const Graph &G); // 图G的广度优先遍历
void MinSpanTree_Prim(const Graph &G); // 输出图G最小生成树 (Prim算法)
void MinSpanTree_Kruskal(const Graph &G); // 输出图G最小生成树 (kruskal算法)
int main()
{
Graph G;
//CreateGraph(G);
CreateGraphByArray(G);
cout << "图的邻接矩阵: " << endl;
PrintGraphArcs(G);
cout << "图的深度优先遍历:";
DFS_Traverse(G);
cout << endl;
cout << "图的广度优先遍历:";
BFS_Traverse(G);
cout << endl;
cout << "最小生成树:(prim算法)" << endl;
MinSpanTree_Prim(G);
cout << endl;
cout << "最小生成树:(kruskal算法)" << endl;
MinSpanTree_Kruskal(G);
cout << endl;
return 0;
}
void CreateGraphByArray(Graph &G)
{
//数据例子取自课本Page168
G.kind = UDG;
const int vn = 6;
VerType V[vn + 1] = {"ABCDEF"};
const int en = 10;
VerType V1[en + 1] = {"ADFEBADFEB"};
VerType V2[en + 1] = {"CCCCCDFEBA"};
ArcType E[en] = {1,5,4,6,5,5,2,6,3,6};
// 输入顶点
G.verNum = vn;
for(int i = 0; i < G.verNum; ++ i){
G.vertex[i] = V[i];
}
// 初始化邻接矩阵
for(int vi = 0; vi < G.verNum; ++ vi){
for(int vj = 0; vj < G.verNum; ++ vj){
G.arcs[vi][vj] = INT_MAX;
}
}
// 输入边
G.arcNum = en;
for(int i = 0; i < G.arcNum; ++ i){
VerType &v1 = V1[i], &v2 = V2[i];
ArcType &e = E[i];
int vi = VertexLoc(G, v1), vj = VertexLoc(G, v2);
if(vi == G.verNum || vj == G.verNum){
continue;
}
if(UDG == G.kind){
G.arcs[vi][vj] = G.arcs[vj][vi] = e;
}else{
G.arcs[vi][vj] = e;
}
}
}
void CreateGraph(Graph &G)
{
// 输入图类型
int k;
cin >> k;
if(k == 0){
G.kind = DG;
}else{
G.kind = UDG;
}
// 输入顶点
cin >> G.verNum;
for(int i = 0; i < G.verNum; ++ i){
cin >> G.vertex[i];
}
// 初始化邻接矩阵
for(int vi = 0; vi < G.verNum; ++ vi){
for(int vj = 0; vj < G.verNum; ++ vj){
G.arcs[vi][vj] = INT_MAX;
}
}
// 输入边
VerType v1, v2; ArcType e;
cin >> G.arcNum;
for(int i = 0; i < G.arcNum; ++ i){
cin >> v1 >> v2 >> e;
int vi = VertexLoc(G, v1), vj = VertexLoc(G, v2);
if(vi == G.verNum || vj == G.verNum){
continue;
}
if(UDG == G.kind){
G.arcs[vi][vj] = G.arcs[vj][vi] = e;
}else{
G.arcs[vi][vj] = e;
}
}
}
int VertexLoc(const Graph &G, const VerType &v)
{
for(int i = 0; i < G.verNum; ++ i){
if(G.vertex[i] == v){
return i;
}
}
return G.verNum;
}
void PrintGraphArcs(const Graph &G)
{
for(int vi = 0; vi < G.verNum; ++ vi){
for(int vj = 0; vj < G.verNum; ++ vj){
if(G.arcs[vi][vj] == INT_MAX){
cout << setw(5) << "INF";
}else{
cout << setw(5) << G.arcs[vi][vj];
}
}
cout << endl;
}
}
void DFS(const Graph G, int vi, bool visited[])
{
cout << G.vertex[vi] << " ";
visited[vi] = true;
for(int vj = 0; vj < G.verNum; ++ vj){
if(G.arcs[vi][vj] != INT_MAX && !visited[vj]){
DFS(G, vj, visited);
}
}
}
void DFS_Traverse(const Graph &G)
{
bool visited[G.verNum];
for(int vi = 0; vi < G.verNum; ++ vi){
visited[vi] = false;
}
for(int vi = 0; vi < G.verNum; ++ vi){
if(!visited[vi]){
DFS(G, vi, visited);
}
}
}
void BFS_Traverse(const Graph &G)
{
bool visited[G.verNum];
for(int i = 0; i < G.verNum; ++ i){
visited[i] = false;
}
for(int i = 0; i < G.verNum; ++ i){
if(!visited[i]){
queue<int> que;
que.push(i);
visited[i] = true;
while(!que.empty()){
int vi = que.front();
cout << G.vertex[vi] << " ";
for(int vj = 0; vj < G.verNum; ++ vj){
if(G.arcs[vi][vj] != INT_MAX && !visited[vj]){
que.push(vj);
visited[vj] = true;
}
}
que.pop();
}
}
}
}
void MinSpanTree_Prim(const Graph &G)
{
//辅助结构, closeedge[i]={j, w}表示顶点vi权值最小的边,vj为边顶点, w为权值
struct
{
int adjvex; // 最小边顶点
ArcType lowcost; // 最小边上的权值
}closedge[G.verNum];
int k = 0;
for(int j = 0; j < G.verNum; ++ j){
if(j != k){
closedge[j] = {k, G.arcs[k][j]};
}
}
closedge[k].lowcost = 0; //表示顶点已经被选入Enew
for(int i = 1; i < G.verNum; ++ i){
/* 从Vnew选取权值最小的边 */
k = -1;
for(int j = 0; j < G.verNum; ++ j){
if(closedge[j].lowcost != 0){
if(k == -1){
k = j;
}else if(closedge[j].lowcost < closedge[k].lowcost){
k = j;
}
}
}
int v0 = k, u0 = closedge[k].adjvex;
cout << G.vertex[u0] << " - " << G.vertex[v0] << endl; //输出边
closedge[k].lowcost = 0; //将该顶点选入Enew
/* 更新与新顶点相连的顶点最小权值 */
for(int j = 0; j < G.verNum; ++ j){
if(G.arcs[k][j] < closedge[j].lowcost){
closedge[j] = {k, G.arcs[k][j]};
}
}
}
}
void MinSpanTree_Kruskal(const Graph &G)
{
//辅助数组 (kruskal算法)
struct
{
int head; // 边的起点
int tail; // 边的终点
ArcType lowcost; // 边上的权值
}edge[G.arcNum], temp;
//初始化edge
if(UDG == G.kind){
for(int i = 0, vi = 0; vi < G.verNum; ++ vi){
for(int vj = 0; vj < vi; ++ vj){
if(G.arcs[vi][vj] != INT_MAX){
edge[i].head = vi;
edge[i].tail = vj;
edge[i ++].lowcost = G.arcs[vi][vj];
}
}
}
}else{
for(int i = 0, vi = 0; vi < G.verNum; ++ vi){
for(int vj = 0; vj < G.verNum; ++ vj){
if(G.arcs[vi][vj] != INT_MAX){
edge[i].head = vi;
edge[i].tail = vj;
edge[i ++].lowcost = G.arcs[vi][vj];
}
}
}
}
//并根据权值从小到大排序
for(int i = 1; i <= G.arcNum; ++ i){
for(int j = 0; j < G.arcNum - i; ++ j){
if(edge[j].lowcost > edge[j + 1].lowcost){
temp = edge[j];
edge[j] = edge[j + 1];
edge[j + 1] = temp;
}
}
}
int vexset[G.verNum];
for(int i = 0; i < G.verNum; ++ i){
vexset[i] = i;
}
for(int i = 0; i < G.arcNum; ++ i){
int vi = edge[i].head, vj = edge[i].tail;
int vs1 = vexset[vi], vs2 = vexset[vj];
if(vs1 != vs2){
cout << G.vertex[vi] << " - " << G.vertex[vj] << endl;
for(int j = 0; j < G.verNum; ++ j){
if(vexset[j] == vs2){
vexset[j] = vs1;
}
}
}
}
}
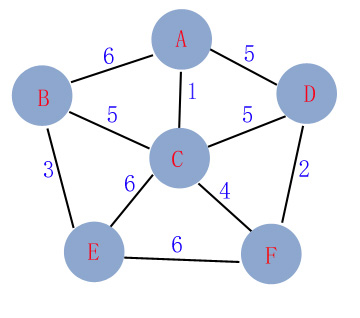
对于这个图:
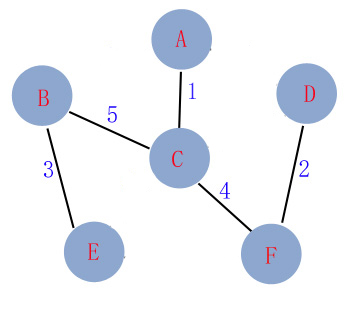
最小生成树的图形为:
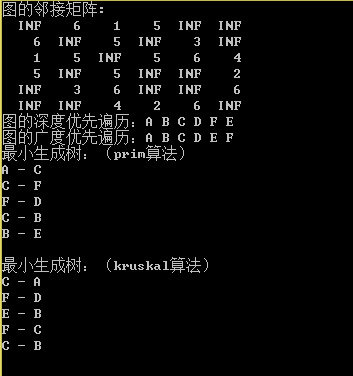
所运行的结果如下:






















 1342
1342

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








