离散对数密码学原理

一 简介

离散对数被誉为当代密码学领域的三大基础之一。1976年，Diffifie和Hellman提出了一种密钥协商协议， 产生了首个离散对数系统模型；8年后，ElGamal提出了基于离散对数系统的公钥加密和签名方法，并奠定了离散对数密码学基础。从那时起，围绕离散对数系统产生了不少研究成果，本文阐述离散对数的基本概念，然后介绍基于离散对数的ElGamal的公钥加密方法和数字签名方法（DSA）。

二 离散对数基本概念

在实数域，对数$x={\log }_{b}a$表示b为底，目标数为a的幂x，换句话说，对数是求幂x的逆运算，使得$b^x=a$。假设指数函数$b^k(k\in I)$的所有元素组成群G，那么离散对数$lo{g}_{b}a$的值必定为整数k，满足 $b^k=a$。可见，离散对数专指满足幂等条件的整数值，属于数论范畴。不失一般性，通过引入索引$in{d}_r$，可以得到一般形式的定义：
$x=in{d}_{r}a(modm)$
其中，r是基本根，m是模数，满足gcd(a,m) = 1（a和m互质）。
基于以上定义，引出离散对数问题，即：给定质数p和正整数g，知道$y=g^x(modp)$的值，求解x。这个问题的求解超过多项式时间，难度是相当大的；反过来，知道x，求解$y=g^x(modp)$的速度却相当快。用一句歌词“爱到尽头，覆水难收”来比喻，像极了泼出去的水，把水泼出去很容易，要将地上的水收回来，超级难！
离散对数加密系统正是利用了这一正反向求解难度不相同的原理。

三 基于离散对数的ElGamal的加密方法

离散对数系统的参数构成一个集合，称为与公共参数域（p,q,g），其中p是一个质数，q是p-1的分解质因数，具有阶数q（群元素的个数称为阶，若p是质数，阶为p-1）。

离散对数密钥的产生

设x为私钥，其值为整数，随机且均匀的从区域[1,q-1]中选取，y为公钥。参考前述定义，离散对数问题（DLP）可描述为给定公共参数域（p,q,g）和y，确定x的问题。具有以下关系：

离散对数参数域产生算法如下。

离散对数参数生成算法

输入：安全参数l（p的长度位数）,t（q的长度位数）.
输出：离散对数参数域（p,q,g）
1.选取长度位数为l的质数p，长度位数为t的质数q，确保q能够整除p-1；
2.选择基本根g，具有阶数q； 
   2.1 选择任意的整数h,范围在[1,p-1],计算 g = h^(p-1)/q ( mod p).
   2.2 如果 g=1，goto 2.1
3. 返回(p,q,g)   

一个栗子
这里举个栗子，作为对以上算法执行流程的复盘：设l 和 t 同为4，即p和q取值不大于15。假设选p为11，q为质数，且能整除11-1=10，因此q等于5。p，q一旦确定，接下来就可以求g了。 根据步骤2.1，g的取值范围在[1，10]，我们从h=1开始逐个数遍历，计算
$g=h^{(p-1)/q}\mathrm{m}\mathrm{o}\mathrm{d}p=h^2\mathrm{m}\mathrm{o}\mathrm{d}11$
通过计算，依次得到这样一组数（h,g）：（$\underline{1，1}$）(2，4) （3，9）（4，5）（5，3）（6，3）（7，5）（8，9）（9，4）（$\underline{10，1}$）。根据步骤2.2，只有第1组和第10组数（黑体下划线）的g=1，不满足选取要求。我们随机取g=3。

下面给出公钥y和私钥x的 产生算法

离散密钥对产生算法：

输入：离散对数公共域(p,q,g)
输出：(y,x)
1. 随机选取私钥x，范围在[1,q-1]
2. 计算 y = g^x mod p
3. 返回(y,x)。在这里插入代码片

继续前一个栗子
在[1,10]的范围内选取x=6，计算$y=3^6\mathrm{m}\mathrm{o}\mathrm{d}11=3$,返回$(x,y)=(6,3)$。

离散对数加密

一切准备就绪，我们现在获得了一组离散对数公有域$(p,q,g)=(11,5,3)$，还在此基础上创建了一个公私钥对$(x,y)=(6,3)$。离散对数加密的基础就建立起来了。下面轮到我们年轻英俊的主角刘英俊出场了。刘英俊和美如花因为仙界诅咒，一直得不到凡间的祝福。地下恋情得以为继，促使男主人公在不公开恋情的同时，还和女主维系着剪不断理还乱的"亲情“和”友情“。那么怎么向如花传递爱的信号呢？
某日，英俊向如花发了一条信息：“爱到尽头，覆水难收”，为了避开邪恶的损友和多情的闺蜜，他用事先约定的数字密码发送：2406（爱死你了），3344（生生世世）。
设y为如花的提供的公钥，英俊利用y将明文m（24063344）转换成密文c1，具体操作为：

其中k=2是英俊随机挑选的随机数。计算的结果是$c_1=24063344\times （3^2\mathrm{m}\mathrm{o}\mathrm{d}11）=216，570，096$。
同时，计算参数c2如下：

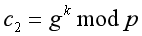
结果是$c_2=3^2\mathrm{m}\mathrm{o}\mathrm{d}11=9$。随后，英俊将（c1,c2）=(216570096, 9)发给如花。如花用珍藏的私钥x=5计算以下同余公式：

得到$c_2=9^6\mathrm{m}\mathrm{o}\mathrm{d}11=531441\mathrm{m}\mathrm{o}\mathrm{d}11=9$。再用$c_2=9$除以c1，就可以计算出明文$m=216570096÷9=2406,3344$。
下面是具体的证明。

基本ElGamal加密算法和解密算法分别描述如下：

基础ElGamal加密算法

基础ElGamal解密算法

美如花回信“爱你在心口难开”，用同样的方式将信息传递英俊。显然，邪恶损友要恢复明文m，须在已知公共域参数（p,q,g）和y的 前提下计算x，难度之大，足以使2人百年好合，白头偕老。这个任务也被成为Diffie-Hellman问题（DHP）。

四 基于离散对数的ElGamal数字签名

数字签名算法（DSA）是美国标准委员会（NIST）于1991年提出的，被指定为美国联邦信息处理标准（FIPS186）。为了进一步描述数字签名算法，假设签名者具有密钥x，他从整数区间[1，q-1]随机选取整数k，计算如下参数：

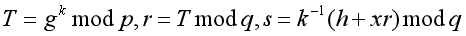
其中h=H(m)是用哈希函数计算的消息摘要。签名者对明文m的签名表示为（r,s）。为验证签名的真实性， 校验者需要根据（r,s）并计算上面公式。然而，校验者没有获得签名者的私钥x和随机数k，自然无法按照公式验签。因此， 需要对上面的公式做一下变形:

将k带入：

得到：

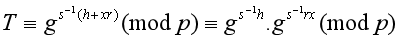
再根据公钥y的定义：

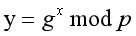
推导出：

验证者因此可以通过上式对T进行校验。
离散对数系统签名算法

离散对数验签的算法

五 总结

离散对数系统建立在有限循环群的基础上，为了增加系统的安全性，人们千方百计扩大质数p的取值范围， 迄今为止，人类发现的已知最大质数是$2^{82,589,933}-1$。然而根据欧拉定理，p的值是无穷的。也许通过不断探索，科学家才能够发现迄今算力需要上亿年才能分解的超大型整数。

[1]: Darrel Hankerson (Author), Alfred J. Menezes (Author), Scott Vanstone (Author)，Guide to Elliptic Curve Cryptography，book，Springer Professional Computing，2003。
[2]: https://en.wikipedia.org/wiki/Discrete_logarithm