密码学基础：离散对数

离散对数系统的参数构成一个集合，称为与公共参数域（p,q,g），其中p是一个质数，q是p-1的分解质因数，具有阶数q（群元素的个数称为阶，若p是质数，阶为p-1）。

质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。质数又称素数。一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数；否则称为合数（规定1既不是质数也不是合数）。

每个合数都可以写成几个质数相乘的形式，其中每个质数都是这个合数的因数，把一个合数用质因数相乘的形式表示出来，叫做分解质因数。如30=2×3×5 。分解质因数只针对合数。

gcd(a,m)=1

a和m的最大公约数是1，就是互素。gcd就是最大公约数的意思。

互质与互素没有区别。

X=logba表示b为底，目标数为a的幂x。

X=indra(mod m) r是基本根，m是模数，满足gcd(a,m) = 1（a和m互质）。

基于以上定义，引出离散对数问题，即：给定质数p和正整数g，知道y = gx(mod p) 的值，求解x。这个问题的求解超过多项式时间，难度是相当大的；反过来，知道x，求解y的速度却相当快。

离散对数密钥的产生

设x为私钥，其值为整数，随机且均匀的从区域[1,q-1]中选取，y为公钥。参考前述定义，离散对数问题（DLP）可描述为给定公共参数域（p,q,g）和y，确定x的问题。具有以下关系：

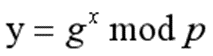
输入：安全参数l（p的长度位数）,t（q的长度位数）.

输出：离散对数参数域（p,q,g）

1.选取长度位数为l的质数p，长度位数为t的质数q，确保q能够整除p-1；

2.选择基本根g，具有阶数q；

   2.1 选择任意的整数h,范围在[1,p-1],计算 g = h^(p-1)/q ( mod p).

   2.2 如果 g=1，goto 2.1

3. 返回(p,q,g) 

例子

作为对以上算法执行流程的复盘：设l 和 t 同为4，即p和q取值不大于15。假设选p为11，q为质数，且能整除11-1=10，因此q等于5。p，q一旦确定，接下来就可以求g了。 根据步骤2.1，g的取值范围在[1，10]，我们从h=1开始逐个数遍历，计算

g=h(p-1)/qmod p = h2 mod 11

通过计算，依次得到这样一组数（h,g）：(1,1)  (2，4) （3，9）（4，5）（5，3）（6，3）（7，5）（8，9）（9，4）(10,1)

根据步骤2.2，只有第1组和第10组数的g=1，不满足选取要求。我们随机取g=3。

下面给出公钥y和私钥x的 产生算法

离散密钥对产生算法：

输入：离散对数公共域(p,q,g)

输出：(y,x)

1. 随机选取私钥x，范围在[1,q-1]

2. 计算 y = g^x mod p

3. 返回(y,x)。在这里插入代码片

继续上面例子

在[1,10]的范围内选取x=6，计算y = 36 mod 11=3,返回( x , y ) = ( 6 , 3 ) (x,y)=(6,3)(x,y)=(6,3)。

利用y将明文m（24063344）转换成密文c1，具体操作为：

 其中k=2是随机数。计算的结果是c 1 = 24063344 ×（32mod11）= 216570096。同时，计算参数c2如下：

 得到c2 = 96 mod 11 = 531441 mod 11 = 9。 发送（c1,c2）=(216570096, 9)

收到消息后，使用私钥x=6计算以下同余公式：

 得到c2=96 mod11=531441 mod 11=9。再用c2除以c1，计算出明文m=216570096/9=24063344

 离散对数系统建立在有限循环群的基础上，为了增加系统的安全性，人们千方百计扩大质数p的取值范围。