Wiki上说的很清楚
A red–black tree is a type of self-balancing binary search tree, a data structure used in computer science.
The self-balancing is provided by painting each node with one of two colors (these are typically called 'red' and 'black', hence the name of the trees) in such a way that the resulting painted tree satisfies certain properties that don't allow it to become significantly unbalanced. When the tree is modified, the new tree is subsequently rearranged and repainted to restore the coloring properties. The properties are designed in such a way that this rearranging and recoloring can be made efficiently.
The balancing of the tree is not perfect but it is good enough to allow it to guarantee searching in O(log n) time, wheren is the total number of elements in the tree. The insertion, and deletion operations, along with the tree rearrangement and recoloring are also performed in O(log n) time.[1]
Tracking the color of each node requires only 1 bit of information per node because there are only two colors. The tree does not contain any other data specific to its being a red–black tree so its memory footprint is almost identical to classic (uncolored) binary search tree. In many cases the additional bit of information can be stored at no additional memory cost.
| Red–black tree | ||
|---|---|---|
| Type | Tree | |
| Invented | 1972 | |
| Invented by | Rudolf Bayer | |
| Time complexity in big O notation | ||
| Average | Worst case | |
| Space | O(n) | O(n) |
| Search | O(log n) | O(log n) |
| Insert | O(log n) | O(log n) |
| Delete | O(log n) | O(log n) |
非常重要的五点特性
In addition to the requirements imposed on a binary search trees, with red–black trees:[4]
- A node is either red or black.
- The root is black. (This rule is sometimes omitted. Since the root can always be changed from red to black, but not necessarily vice-versa, this rule has little effect on analysis.)
- All leaves (NIL) are black. (All leaves are same color as the root.)
- Both children of every red node are black.
- Every simple path from a given node to any of its descendant leaves contains the same number of black nodes.
关于红黑树的插入操作很经典,有算法导论上的非递归版本和wiki上的递归版本,从理解上看wiki上的更容易理解,但是算法导论上的更简洁,最好结合着读,先读懂wiki上的版本在读算法导论上的版本就很容易了。
算法导论上的非递归版本源码:
RB-INSERT(T, z)
y ← nil[T]
x ← root[T]
while x ≠ nil[T]
do y ← x
if key[z] < key[x]
then x ← left[x]
else x ← right[x]
p[z] ← y
if y = nil[T]
then root[T] ← z
else if key[z] < key[y]
then left[y] ← z
else right[y] ← z
left[z] ← nil[T]
right[z] ← nil[T]
color[z] ← RED
RB-INSERT-FIXUP(T, z)RB-Insert-fixup函数在原来的伪代码的基础上做了修改
RB-INSERT-FIXUP(T, z)
{
while color[p[z]] == RED
{
if p[z] == left[p[p[z]]]
{
y ← right[p[p[z]]]
if color[y] == RED
{ color[p[z]] ← BLACK
color[y] ← BLACK
color[p[p[z]]] ← RED
z ← p[p[z]]
}else
{
if z == right[p[z]]
{ z ← p[z]
LEFT-ROTATE(T, z)
}
color[p[z]] ← BLACK
color[p[p[z]]] ← RED
RIGHT-ROTATE(T, p[p[z]])
}
}
else (same as then clause
with "right" and "left" exchanged)
}
color[root[T]] ← BLACK
}以下是wiki上的递归版本:
Insertion
Insertion begins by adding the node as any binary search tree insertion does and by coloring it red. Whereas in the binary search tree, we always add a leaf, in the red–black tree leaves contain no information, so instead we add a red interior node, with two black leaves, in place of an existing black leaf.
What happens next depends on the color of other nearby nodes. The term uncle node will be used to refer to the sibling of a node's parent, as in human family trees. Note that:
- property 3 (all leaves are black) always holds.
- property 4 (both children of every red node are black) is threatened only by adding a red node, repainting a black node red, or a rotation.
- property 5 (all paths from any given node to its leaf nodes contain the same number of black nodes) is threatened only by adding a black node, repainting a red node black (or vice versa), or a rotation.
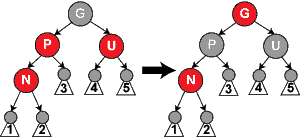
- Note: The label N will be used to denote the current node (colored red). At the beginning, this is the new node being inserted, but the entire procedure may also be applied recursively to other nodes (see case 3). P will denote N's parent node, G will denote N's grandparent, and U will denote N's uncle. Note that in between some cases, the roles and labels of the nodes are exchanged, but in each case, every label continues to represent the same node it represented at the beginning of the case. Any color shown in the diagram is either assumed in its case or implied by those assumptions. A numbered triangle represents a subtree of unspecified depth. A black circle atop the triangle designates a black root node, otherwise the root node's color is unspecified.
Each case will be demonstrated with example C code. The uncle and grandparent nodes can be found by these functions:
struct node *grandparent(struct node *n) { if ((n != NULL) && (n->parent != NULL)) return n->parent->parent; else return NULL; } struct node *uncle(struct node *n) { struct node *g = grandparent(n); if (g == NULL) return NULL; // No grandparent means no uncle if (n->parent == g->left) return g->right; else return g->left; }
Case 1: The current node N is at the root of the tree. In this case, it is repainted black to satisfy property 2 (the root is black). Since this adds one black node to every path at once, property 5 (all paths from any given node to its leaf nodes contain the same number of black nodes) is not violated.
void insert_case1(struct node *n) { if (n->parent == NULL) n->color = BLACK; else insert_case2(n); }
Case 2: The current node's parent P is black, so property 4 (both children of every red node are black) is not invalidated. In this case, the tree is still valid. property 5 (all paths from any given node to its leaf nodes contain the same number of black nodes) is not threatened, because the current node N has two black leaf children, but because N is red, the paths through each of its children have the same number of black nodes as the path through the leaf it replaced, which was black, and so this property remains satisfied.
void insert_case2(struct node *n) { if (n->parent->color == BLACK) return; /* Tree is still valid */ else insert_case3(n); }
- Note: In the following cases it can be assumed that N has a grandparent node G, because its parent P is red, and if it were the root, it would be black. Thus, N also has an uncle node U, although it may be a leaf in cases 4 and 5.
|
Case 3: If both the parent P and the uncle U are red, then both of them can be repainted black and the grandparentG becomes red (to maintain property 5 (all paths from any given node to its leaf nodes contain the same number of black nodes)). Now, the current red node N has a black parent. Since any path through the parent or uncle must pass through the grandparent, the number of black nodes on these paths has not changed. However, the grandparent G may now violate properties 2 (The root is black) or 4 (Both children of every red node are black) (property 4 possibly being violated since G may have a red parent). To fix this, the entire procedure is recursively performed on G from case 1. Note that this is a tail-recursive call, so it could be rewritten as a loop; since this is the only loop, and any rotations occur after this loop, this proves that a constant number of rotations occur. |
void insert_case3(struct node *n) { struct node *u = uncle(n), *g; if ((u != NULL) && (u->color == RED)) { n->parent->color = BLACK; u->color = BLACK; g = grandparent(n); g->color = RED; insert_case1(g); } else { insert_case4(n); } }
- Note: In the remaining cases, it is assumed that the parent node P is the left child of its parent. If it is the right child, left and right should be reversed throughout cases 4 and 5. The code samples take care of this.
|
Case 4: The parent P is red but the uncle U is black; also, the current node N is the right child of P, and P in turn is the left child of its parent G. In this case, a left rotation that switches the roles of the current node Nand its parent P can be performed; then, the former parent node P is dealt with using case 5 (relabeling N and P) because property 4 (both children of every red node are black) is still violated. The rotation causes some paths (those in the sub-tree labelled "1") to pass through the node N where they did not before. It also causes some paths (those in the sub-tree labelled "3") not to pass through the node P where they did before. However, both of these nodes are red, so property 5 (all paths from any given node to its leaf nodes contain the same number of black nodes) is not violated by the rotation. After this case has been completed, property 4 (both children of every red node are black) is still violated, but now we can resolve this by continuing to case 5. |
void insert_case4(struct node *n) { struct node *g = grandparent(n); if ((n == n->parent->right) && (n->parent == g->left)) { rotate_left(n->parent); n = n->left; } else if ((n == n->parent->left) && (n->parent == g->right)) { rotate_right(n->parent); n = n->right; } insert_case5(n); }
|
Case 5: The parent P is red but the uncle U is black, the current node N is the left child of P, and P is the left child of its parent G. In this case, a right rotation on G is performed; the result is a tree where the former parent P is now the parent of both the current node N and the former grandparent G. G is known to be black, since its former child P could not have been red otherwise (without violating property 4). Then, the colors of Pand G are switched, and the resulting tree satisfies property 4 (both children of every red node are black). Property 5 (all paths from any given node to its leaf nodes contain the same number of black nodes) also remains satisfied, since all paths that went through any of these three nodes went through G before, and now they all go through P. In each case, this is the only black node of the three. |
void insert_case5(struct node *n) { struct node *g = grandparent(n); n->parent->color = BLACK; g->color = RED; if (n == n->parent->left) rotate_right(g); else rotate_left(g); }
Note that inserting is actually in-place, since all the calls above use tail recursion.
删除操作:
最重要的是要彻底理解好红黑树的叶节点的概念,所有的叶节点和根的父亲都用一个sentinel node(哨兵)表示。如下图,在二叉树中结点6,11,15,22,27为叶子,但是在红黑树中所有的NIL才为叶子, 6,11,15,22,27均非叶子。即红黑树中的结点只分为内部结点(有两个子)和叶子结点(无子)。
The leaf nodes of red–black trees do not contain data. These leaves need not be explicit in computer memory—a null child pointer can encode the fact that this child is a leaf—but it simplifies some algorithms for operating on red–black trees if the leaves really are explicit nodes. To save memory, sometimes a single sentinel node performs the role of all leaf nodes; all references from internal nodes to leaf nodes then point to the sentinel node.
Non-leaf children, rather than all children, are specified here because unlike normal binary search trees, red–black trees have leaf nodes anywhere they can have them, so that all nodes are either internal nodes with two children or leaf nodes with, by definition, zero children. In effect, internal nodes having two leaf children in a red–black tree are like the leaf nodes in a regular binary search tree. 
算法导论上的非递归算法
RB-Delete(T,z)
if left[z] = nil[T] or right[z] = nil[T]
then y<-z
else y<- Tree-successor(z)
if left[y]!= nil[T]
then x<- left[y]
else x<- right[y]
p[x]<- p[y]
if p[y] = nil[T]
then root[T] <-x
else if y=left[p[y]]
then left[p[y]] <-x
else right[p[y]] <- x
if y!=x
then key[z] <- key[y]
copy y's satellite data into z
if color[y] = black
then RB-Delete-fixup(T,x)
return y
RB-Delete-fixup(T,x)
while x!=root[T] and color[x]=black
do if x= left[p[x]]
then w <- right[p[x]]
if color[w]=red
then color[w] <- black
color[p[x]] <- red
left-Rotate(T,p[x])
w<-right[p[x]]
if color[left[w]]=black and color[right[w]]=black
then color[w]<-red
x<- p[x]
else if color[right[w]] = black
then color[left[w]] <- black
color[w] <- red
right-Rotate(T,w)
w<-right[p[x]]
color[w]<-color[p[x]]
color[p[x]]<- black
color[right[w]]<-black
left-Rotate(T,p[x])
x<-root[T]
else (same as then clause with 'right' and 'left' exchanged
color[x]<-black Wiki上的删除解释,以及递归删除操作
Removal
In a regular binary search tree when deleting a node with two non-leaf children, we find either the maximum element in its left subtree (which is the in-order predecessor) or the minimum element in its right subtree (which is the in-order successor) and move its value into the node being deleted (as shown here). We then delete the node we copied the value from, which must have fewer than two non-leaf children. Because merely copying a value does not violate any red–black properties, this reduces to the problem of deleting a node with at most one non-leaf child. Once we have solved that problem, the solution applies equally to the case where the node we originally want to delete has at most one non-leaf child as to the case just considered where it has two non-leaf children.
Therefore, for the remainder of this discussion we address the deletion of a node with at most one non-leaf child. We use the label M to denote the node to be deleted; C will denote a selected child of M, which we will also call "its child". If M does have a non-leaf child, call that its child,C; otherwise, choose either leaf as its child, C.
If M is a red node, we simply replace it with its child C, which must be black by property 4. (This can only occur when M has two leaf children, because if the red node M had a black non-leaf child on one side but just a leaf child on the other side, then the count of black nodes on both sides would be different, thus the tree would violate property 5.) All paths through the deleted node will simply pass through one less red node, and both the deleted node's parent and child must be black, so property 3 (all leaves are black) and property 4 (both children of every red node are black) still hold.
Another simple case is when M is black and C is red. Simply removing a black node could break Properties 4 (“Both children of every red node are black”) and 5 (“All paths from any given node to its leaf nodes contain the same number of black nodes”), but if we repaint C black, both of these properties are preserved.
The complex case is when both M and C are black. (This can only occur when deleting a black node which has two leaf children, because if the black node M had a black non-leaf child on one side but just a leaf child on the other side, then the count of black nodes on both sides would be different, thus the tree would have been an invalid red–black tree by violation of property 5.) We begin by replacing M with its child C. We will call (or label—that is, relabel) this child (in its new position) N, and its sibling (its new parent's other child) S. (S was previously the sibling of M.) In the diagrams below, we will also use P for N's new parent (M's old parent), SL for S's left child, and SR for S's right child (Scannot be a leaf because if M and C were black, then P's one subtree which included M counted two black-height and thus P's other subtree which includes S must also count two black-height, which cannot be the case if S is a leaf node).
- Note: In between some cases, we exchange the roles and labels of the nodes, but in each case, every label continues to represent the same node it represented at the beginning of the case. Any color shown in the diagram is either assumed in its case or implied by those assumptions. White represents an unknown color (either red or black).
We will find the sibling using this function:
struct node *sibling(struct node *n) { if (n == n->parent->left) return n->parent->right; else return n->parent->left; }
- Note : In order that the tree remains well-defined, we need that every null leaf remains a leaf after all transformations (that it will not have any children). If the node we are deleting has a non-leaf (non-null) child N , it is easy to see that the property is satisfied. If, on the other hand, N would be a null leaf, it can be verified from the diagrams (or code) for all the cases that the property is satisfied as well. 这一段对理解以下的算法很重要,说明无论N是否是叶子以下算法都是满足的。
We can perform the steps outlined above with the following code, where the function replace_node substitutes child into n's place in the tree. For convenience, code in this section will assume that null leaves are represented by actual node objects rather than NULL (the code in the Insertionsection works with either representation).
void delete_one_child(struct node *n) { /* * Precondition: n has at most one non-null child. */ struct node *child = is_leaf(n->right) ? n->left : n->right; replace_node(n, child); if (n->color == BLACK) { if (child->color == RED) child->color = BLACK; else delete_case1(child); } free(n); }
-
Note: If
N is a null leaf and we do not want to represent null leaves as actual node objects, we can modify the algorithm by first calling delete_case1() on its parent (the node that we delete,
nin the code above) and deleting it afterwards. We can do this because the parent is black, so it behaves in the same way as a null leaf (and is sometimes called a 'phantom' leaf). And we can safely delete it at the end asnwill remain a leaf after all operations, as shown above.
If both N and its original parent are black, then deleting this original parent causes paths which proceed through N to have one fewer black node than paths that do not. As this violates property 5 (all paths from any given node to its leaf nodes contain the same number of black nodes), the tree must be rebalanced. There are several cases to consider: Case 1, 3, 4 is easy to understand.
Case 1: N is the new root. In this case, we are done. We removed one black node from every path, and the new root is black, so the properties are preserved.
void delete_case1(struct node *n) { if (n->parent != NULL) delete_case2(n); }
- Note: In the descriptions of cases 2, 5, and 6, we assume N is the left child of its parent P. If it is the right child, left and right should be reversed throughout these three cases. However, the code examples take both cases into account.
|
Case 2: S is red (P has to be black as it had a red child). (Why reverse the nodes color and rotate left ??? )In this case we reverse the colors of P and S, and then rotate left at P, turning Sinto N's grandparent. Although all paths still have the same number of black nodes, now N has a black sibling and a red parent, so we can proceed to step 4, 5, or 6. (Its new sibling is black because it was once the child of the red S.) In later cases, we will relabel N's new sibling as S. 注意case2并未使得通过P再经过N的Black Height得到补偿,所以仍然需要经历其他Step, 比如step 4就可以让Black Height得到补偿。
|
void delete_case2(struct node *n) { struct node *s = sibling(n); if (s->color == RED) { n->parent->color = RED; s->color = BLACK; if (n == n->parent->left) rotate_left(n->parent); else rotate_right(n->parent); } delete_case3(n); }
|
Case 3: P, S, and S's children are black. Because deleting N's original parent made all paths passing through N have one less black node, this evens things up. so in this case, we simply repaint S red, then the result is that all paths passing through S, which are precisely those paths not passing through N, have one less black node. However, all paths through P now have one fewer black node than paths that do not pass through P, so property 5 (all paths from any given node to its leaf nodes contain the same number of black nodes) is still violated. To correct this, we perform the rebalancing procedure on P, starting at case 1. |
void delete_case3(struct node *n) { struct node *s = sibling(n); if ((n->parent->color == BLACK) && (s->color == BLACK) && (s->left->color == BLACK) && (s->right->color == BLACK)) { s->color = RED; delete_case1(n->parent); } else delete_case4(n); }
|
Case 4: S and S's children are black, but P is red. Because deleting N's original parent made all paths passing through N have one less black node, this evens things up, so in this case, we simply exchange the colors of Sand P.This does not affect the number of black nodes on paths going through S, but it does add one to the number of black nodes on paths going through N, making up for the deleted black node on those paths. |
void delete_case4(struct node *n) { struct node *s = sibling(n); if ((n->parent->color == RED) && (s->color == BLACK) && (s->left->color == BLACK) && (s->right->color == BLACK)) { s->color = RED; n->parent->color = BLACK; } else delete_case5(n); }
|
Case 5: S is black, S's left child is red, S's right child is black, and N is the left child of its parent. In this case we rotate right at S, so that s left child becomes S's parent and N's new sibling. We then exchange the colors of S and its new parent. All paths still have the same number of black nodes, but now N has a black sibling whose right child is red, so we fall into case 6. Neither N nor its parent are affected by this transformation. (Again, for case 6, we relabel N's new sibling as S.) |
void delete_case5(struct node *n) { struct node *s = sibling(n); if (s->color == BLACK) { /* the following statements just force the red to be on the left of the left of the parent, or right of the right, so case 6 will rotate correctly. */ if ((n == n->parent->left) && (s->right->color == BLACK) && (s->left->color == RED)) { s->color = RED; s->left->color = BLACK; rotate_right(s); } else if ((n == n->parent->right) && (s->left->color == BLACK) && (s->right->color == RED)) { s->color = RED; s->right->color = BLACK; rotate_left(s); } } delete_case6(n); }
|
Case 6: S is black, S's right child is red, and N is the left child of its parent P. In this case we rotate left at P, so that S becomes the parent of P and S's right child. We then exchange the colors of P and S, and make S's right child black. The subtree still has the same color at its root, so Properties 4 (Both children of every red node are black) and 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) are not violated.However, N now has one additional black ancestor: either P has become black, or it was black and S was added as a black grandparent. Thus, the paths passing through N pass through one additional black node. Meanwhile, if a path does not go through N, then there are two possibilities:
Either way, the number of black nodes on these paths does not change. Thus, we have restored Properties 4 (Both children of every red node are black) and 5 (All paths from any given node to its leaf nodes contain the same number of black nodes). The white node in the diagram can be either red or black, but must refer to the same color both before and after the transformation. |
void delete_case6(struct node *n) { struct node *s = sibling(n); s->color = n->parent->color; n->parent->color = BLACK; if (n == n->parent->left) { s->right->color = BLACK; rotate_left(n->parent); } else { s->left->color = BLACK; rotate_right(n->parent); } }
Again, the function calls all use tail recursion, so the algorithm is in-place. In the algorithm above, all cases are chained in order, except in delete case 3 where it can recurse to case 1 back to the parent node: this is the only case where an in-place implementation will effectively loop (after only one rotation in case 3).
Additionally, no tail recursion ever occurs on a child node, so the tail recursion loop can only move from a child back to its successive ancestors. No more than O(log n) loops back to case 1 will occur (where n is the total number of nodes in the tree before deletion). If a rotation occurs in case 2 (which is the only possibility of rotation within the loop of cases 1–3), then the parent of the node N becomes red after the rotation and we will exit the loop. Therefore at most one rotation will occur within this loop. Since no more than two additional rotations will occur after exiting the loop, at most three rotations occur in total.
Only Case 1,4 and 6 is 终极杀人王,这三个Case都会在通过N的node上增加一个Black Height,而其他case都未改变经过N的node的black height,所以都要最终调用1,4,6,使得Black Height得到增加1,进而可以补偿因为删除M而导致的原来经过M和N的Black Height. 而操作的小结如下:
从N是黑色出发(1)N是根;(2)S为红,若N为P左子,则对P左旋,反之右旋,然后继续调用下一Step;(3)N,P,S,SL,SR 都黑,染S为红,从Case1再开始;(4)P为红(S为黑),互换S与P颜色;(5)S为黑,不管P的颜色,若N为左子并且S左子为红(右子为黑),将S右旋,并互换S和S左子颜色;若N为右子并且S的右子为红(左子为黑),则对S左旋,并互换S与S右子的颜色;再继续调用下一Step(6)若N为左子,S右子为红,左旋P,并互换P与S的颜色,若N为右子,S左子为红,则右旋P,并互换P与S的颜色。
关于左旋和右旋, some one on stackoverflow says the magic of the ratation as below:
For the benefit of anybody else reading this thread who doesn't have access to the book mentioned in the accepted answer, here is what I hope will be an acceptable descriptive answer.
Rotating puts the tree in a state where it meets the criteria to recolor (the child node has a red uncle). There are two key differences:
- which node is the "child" and which node is the "uncle" has changed;
- instead of recoloring the parent and uncle to black and the grandparent to red, you recolor the parent to red, and the grandparent to black.
When the child node doesn't have a red uncle, you have to rotate because if the uncle node is already black, then making the parent black would increase the black height by 1 on only one side of the grandparent. This would violate the height invariant property of red-black trees and make the tree unbalanced.
Now let's look at how the rotation transforms the tree so that we have a child node with a red uncle and can use recoloring. I recommend drawing this out to fully understand it.
- Let x be the current red node with a red parent.
- Let p be the red parent of x before the rotation (if the parent was black, we'd be done already).
- Let y be the black uncle of x before the rotation (if the uncle was red, we wouldn't need a rotation. We'd simply recolor the parent and uncle to black and the grandparent to red).
- Let g be the black grandparent of x before the rotation (since the parent is red, the grandparent must be black; otherwise this was not a red-black tree to begin with.)
- When you have a left-left (LL) or right-right (RR) case (that is, x is the left child of p and p is the left child of g OR x is the right child of p and p is the right child of g), after a single rotation (right if LL, left if RR), y becomes the child and x its uncle. Since x is a red uncle, you now have a case where you can recolor. So, recolor the parent of the child (since the child is now y, its parent is g) to red, and the child's grandparent (which is now p) to black.
- When you have an LR (x is the left child or p and p is the right child of g) or RL case (x is the right child of p and p is the left child of g), after a double rotation (right then left if LR, left then right if RL), y becomes the child and p its uncle. Since p is a red uncle, you again have a case where you can recolor. So, recolor the parent (since the child is now y, its parent is g) to red, and the child's grandparent (which is now x) to black.
Before the rotation and recoloring, you had a black grandparent with 2 red nodes and 0 black nodes on side A (left or right) and 0 red nodes and 1 black node on side B (the opposite of side A). After the rotation and recoloring, you have a black grandparent with 1 red node and 0 black nodes on side A and 1 red node and 1 black node on side B. So you essentially moved one of the red nodes to the other sub-tree of the grandparent without increasing the black height of either sub-tree.
That's the magic of rotation. It allows you to move the extra red node to another branch without changing the black height, and still preserving the sorted traversal property of a binary search tree.
http://stackoverflow.com/questions/9469858/how-to-easily-remember-red-black-tree-insert-and-delete
http://www.cse.ohio-state.edu/~gurari/course/cis680/cis680Ch11.html
http://en.wikipedia.org/wiki/Red_black_tree
http://www.d.umn.edu/~gshute/ds/rbtrees.html




























 5739
5739

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








