动态规划(详解 带例子)

动态规划之实例一

如果我们有面值为1元、3元和5元的硬币若干枚，如何用最少的硬币凑够11元？ (表面上这道题可以用贪心算法，但贪心算法无法保证可以求出解，比如1元换成2元的时候)

首先我们思考一个问题，如何用最少的硬币凑够i元(i<11)？为什么要这么问呢？ 两个原因：1.当我们遇到一个大问题时，总是习惯把问题的规模变小，这样便于分析讨论。 2.这个规模变小后的问题和原来的问题是同质的，除了规模变小，其它的都是一样的， 本质上它还是同一个问题(规模变小后的问题其实是原问题的子问题)。

好了，让我们从最小的i开始吧。当i=0，即我们需要多少个硬币来凑够0元。 由于1，3，5都大于0，即没有比0小的币值，因此凑够0元我们最少需要0个硬币。 (这个分析很傻是不是？别着急，这个思路有利于我们理清动态规划究竟在做些什么。) 这时候我们发现用一个标记来表示这句“凑够0元我们最少需要0个硬币。”会比较方便， 如果一直用纯文字来表述，不出一会儿你就会觉得很绕了。那么， 我们用d(i)=j来表示凑够i元最少需要j个硬币。于是我们已经得到了d(0)=0， 表示凑够0元最小需要0个硬币。当i=1时，只有面值为1元的硬币可用， 因此我们拿起一个面值为1的硬币，接下来只需要凑够0元即可，而这个是已经知道答案的， 即d(0)=0。所以，d(1)=d(1-1)+1=d(0)+1=0+1=1。当i=2时， 仍然只有面值为1的硬币可用，于是我拿起一个面值为1的硬币， 接下来我只需要再凑够2-1=1元即可(记得要用最小的硬币数量)，而这个答案也已经知道了。 所以d(2)=d(2-1)+1=d(1)+1=1+1=2。一直到这里，你都可能会觉得，好无聊， 感觉像做小学生的题目似的。因为我们一直都只能操作面值为1的硬币！耐心点， 让我们看看i=3时的情况。当i=3时，我们能用的硬币就有两种了：1元的和3元的( 5元的仍然没用，因为你需要凑的数目是3元！5元太多了亲)。 既然能用的硬币有两种，我就有两种方案。如果我拿了一个1元的硬币，我的目标就变为了： 凑够3-1=2元需要的最少硬币数量。即d(3)=d(3-1)+1=d(2)+1=2+1=3。 这个方案说的是，我拿3个1元的硬币；第二种方案是我拿起一个3元的硬币， 我的目标就变成：凑够3-3=0元需要的最少硬币数量。即d(3)=d(3-3)+1=d(0)+1=0+1=1. 这个方案说的是，我拿1个3元的硬币。好了，这两种方案哪种更优呢？ 记得我们可是要用最少的硬币数量来凑够3元的。所以， 选择d(3)=1，怎么来的呢？具体是这样得到的：d(3)=min{d(3-1)+1, d(3-3)+1}。

<span style="color:#333333;">package com.dp;
</span><span style="color:#ff0000;">//应该可以优化，求大神指教</span><span style="color:#333333;">
public class TheMinestCoin {

	/**
	 * @param args
	 */
	// 动态规划  所得出的值与前面的相关，即当前子问题的解由上一问题推出,由上一状态迁移到当前状态，受前面状态的影响
	//这是与分支法的本质区别 分治法没有状态迁移  分治法的子问题不受前面结果的影响
	/*
	 * 当硬币为零时
	 * d(0)=0
	 * d(1)=d(1-1)+1
	 * d(2)=d(2-1)+1
	 * d(3)=d(3-1)+1
	 * 
	 * d(3)=d(3-3)+1;
	 * d(3)=min{d(3-1)+1,d(3-3)+1};//取硬币个数的最小值 动态规划
	 */
	public static void main(String[] args) {
		int a[] = { 1, 3, 5 };

		// 最少需要几枚硬币
		int count=11;
		NumberOfCoin(a, count);
	}

	private static void NumberOfCoin(int[] a, int count) {
		int Min[]=new int[count+1];//储存该硬币所需硬币的最小数目
		Min[0]=0;//
		int minCoin=0;//
		for(int i=1;i<Min.length;i++)
		{
			minCoin=i ;//i是不可变的，每一个都是和前一个相关的
			/*
			 * 求出了最小硬币的个数
			 */
			for(int j=0;j<a.length;j++)
			{
				if(a[j]<=i && Min[i-a[j]]+1<minCoin)// 此处</span><span style="color: rgb(51, 51, 51); font-family: 'Helvetica Neue', Helvetica, Arial, sans-serif;">d(3)=min{d(3-1)+1,d(3-3)+1}</span><span style="color:#333333;">
				{
					minCoin=Min[i-a[j]]+1;
				}
			}
			System.out.println(minCoin + "   i="+i);
			Min[i]=minCoin;//时间复杂度为O(n^2)
		}
		System.out.println(Min[11]);
	}

}
</span>

实例2 动态规划之最长递增子序列

<span style="font-size:14px;">package com.dp;

public class TheLargestIncreamentSubString {

	/**
	 * 假设序列为 5,3,4,8,6,7
	 * d(0)=1;
	 * d(1)=1;因为5>3
	 * d(2)=d(1)+1;4>3
	 * d(3)=d(2)+1;
	 * d(4)=1;因为6<8;
	 * d(5)=d(4)+1;因为7>6 
	 * 则最大递增子序列为d(i) = max{1, d(j)+1},其中j<i,A[j]<=A[i];
	 * 
	 */
	public static void main(String[] args) {
		int a[]={5,3,4,8,6,7};//
		int LIS[]=new int[a.length];//全部都是负数时怎么样？？
		for(int i=0;i<a.length;i++)
		{
			LIS[i]=1;
			for(int j=0;j<=i;j++)
			{
				if(a[j]<a[i] && LIS[j]+1>LIS[i])
				{
					LIS[i]=LIS[j]+1;
				}
			}
		}
		int max=LIS[0];
		for(int i=1;i<LIS.length;i++)
		{
			if(LIS[i]>max)
			{
				max=LIS[i];
			}
		}
		System.out.println(max);
		//时间复杂度为o(n^2);
		//优化
		LISS(a);
	}

	private static void LISS(int[] a) {
		//前面的是顺序查找，我们改为二分查找，这样就可以把时间复杂度降低到nlogn
		int LIS[]=new int[a.length];
		LIS[0]=-10000;//假设所有数组中的元素都比该数大（标识数）
		LIS[1]=a[0];//开始时
		int low,mid,high;
		int len=1;
		for(int i=0;i<a.length;i++)
		{
			low=0;
			high=len;//LIS数组当前数组有元素的实际长度即 0和1
			while(low<=high)
			{
				mid=(low+high)>>1;
			    if(a[i]>LIS[mid])
			    {
			        low=mid+1;
			    	
			    }else
			    {
			    	high=mid-1;
			    }
			}
			LIS[low]=a[i];
			if(low>len)len++;
		}
		for(int i=1;i<=len;i++)
		{
			System.out.print(LIS[i]+"  ");
		}	
	}	
</span><span style="font-size:24px;">}
</span>

3.最大子数组和

public class TheLargestSubHe {

	/**
	 * @param args
	 */
	public static void main(String[] args) {
		//int a[]={-5,2,7,-4,10,3,-2,1}; 
		int a[]={1,-2,3,10,-4,7,2,-5}; 
        MaxSubSum(a);
	}

	private static void MaxSubSum(int[] a) {
		int nAll=0,ntotal=0;
		for(int i=0;i<a.length;i++)
		{
			ntotal=max(ntotal+a[i],a[i]);
			nAll=max(ntotal,nAll);
		}
		System.out.println(nAll);
	}

	private static int max(int i, int j) {
		// TODO Auto-generated method stub
		return i>j?i:j;
	}

}

最长公共子序列

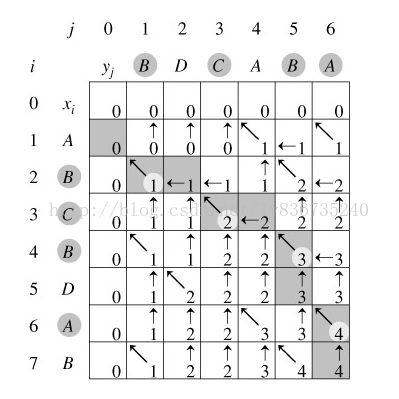
引进一个二维数组c[][]，用c[i][j]记录X[i]与Y[j] 的LCS 的长度，b[i][j]记录c[i][j]是通过哪一个子问题的值求得的，以决定搜索的方向。
我们是自底向上进行递推计算，那么在计算c[i,j]之前，c[i-1][j-1]，c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据X[i] = Y[j]还是X[i] != Y[j]，就可以计算出c[i][j]。

递归式

图解

public class TheLargestCommonMehtod {
	static int count = 0;

	public static void main(String[] args) {
		String a = " abcbdab";
		String b = " bdcaba";
		
		int c[][] = new int[a.length()][b.length()];
		// 最长公共子序列为 而不是最长公共子串
		theLCS(a, b, c);
		// 打印输出最长公共子序列
		println(a.length()-1, b.length()-1, a, c);
		///System.out.println("*******************************");
		for(int i=1;i<c.length;i++)
		{
			for(int j=1;j<c[0].length;j++)
			{
				System.out.print(c[i][j]+" ");
			}
			System.out.println();
		}
	}

	private static void println(int i, int j, String a, int[][] c) {
		if (i == 0 || j == 0)
			return;
		if (c[i][j] == 1) {
			println(i - 1, j - 1, a, c);
			System.out.print(a.charAt(i) + " ");
			
		}
		if (c[i][j] == 2) {
			println(i - 1, j, a, c);
		} else if(c[i][j]==3){
			println(i, j - 1, a, c);
		}
	}

	private static void theLCS(String a, String b, int[][] m) {
		// System.out.println(a.length());
		if (a == null || b == null || a == " " || b == " ")
			return;
		int c[][] = new int[a.length()][b.length()];// 默认值都为零
		//都从1开始 默认忽略掉第一个元素了，所以我在字符串中添加了一个空格，代表第一个相同，但不参与结果
		for (int i = 1; i < a.length(); i++) {
			for (int j = 1; j < b.length(); j++) {
				if (a.charAt(i) == b.charAt(j)) {
					c[i][j] = c[i - 1][j - 1] + 1;
					m[i][j] = 1;
				} else if (c[i - 1][j] > c[i][j - 1]) {
					c[i][j] = c[i - 1][j];
					m[i][j] = 2;
				} else {
					c[i][j] = c[i][j - 1];
					m[i][j] = 3;
				}
			}
		}
		for (int i = 1; i < a.length(); i++) {
			for (int j = 1; j < b.length(); j++) {
				System.out.print(c[i][j] + "  ");
			}
			System.out.println();
		}

	}
}