线段树小结

最新推荐文章于 2023-05-02 16:38:24 发布
置顶 最新推荐文章于 2023-05-02 16:38:24 发布
阅读量1.2k 收藏 3
点赞数
分类专栏： 学习小结 数据结构 - 线段树 文章标签： 线段树小结
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/lwt36/article/details/50255129
版权

线段树小结 A Summary for Segment Tree

0. Anouncement

本文部分图片以及部分内容来自互联网，内容过多就不一一注明出处了，冒犯之处还请海涵。
Some of the pictures and the content of the text come from the Internet.
Due to plenty of the content,there will be no quotation. If offended, please try to forgive me.

Ⅰ. 线段树

  • 什么是线段树？
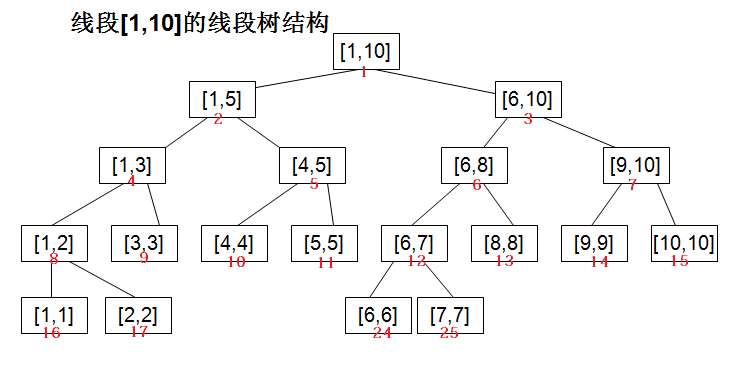
    首先我们来看一个图， 线段树就是每个节点维护一个区间的树。
    可以常数倍空间复杂度的情况下高效的 维 护信息(维护一般指的是更新和查询) 。
    本文除特别题目外，区间以及根节点的下标均从 1 开始，线段树的维护信息均以数组的方法存储。
    线段树

  • 线段树的时空复杂度
    由上图我们可以发现: 线段树维护的区间在同一高度上是完全不相交的，并且恰好包含了所有的区间。
    图中红字所表示的是每个节点的所在的数组的下标
    我们可以发现每个节点的左儿子是父亲节点下标 * 2，右儿子是父亲节点下标 * 2 + 1
    并且我们也发现以这样的存储方式，仅仅开2倍的空间是不够的，4倍才是合适的
    至于为什么是4倍？详情可以看这里，点击查看
    由于线段树的二叉树形结构，更新和查询的时间复杂度操作都是O(logn)

Ⅱ. 线段树的代码模版

  • l,r,rt: 保存的区间信息，其中rt是这个区间信息所存的节点的下标
    L,R: 每次操作要更新的区间
    v: 更新的值
    HH风格的线段树，感谢HH大牛对于线段树学习的分享

  • 单点更新 区间查询(单点查询其实就是区间查询的特例)
    push_up 把儿子节点的信息更新到自己 

//以单点更新 区间查询的RMQ为例
const int N = 1e5 + 10;

#define root 1, n, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1

int maxv[N << 2];

void push_up(int rt) {
    maxv[rt] = max(maxv[rt << 1], maxv[rt << 1 | 1]);
}
void build(int l, int r, int rt) {
    if(l == r) {
        scanf("%d", &maxv[rt]);
        return;
    }
    int m = l + r >> 1;
    build(lson);
    build(rson);
    push_up(rt);
}
void update(int o, int v, int l, int r, int rt) {
    if(l == r) {
        maxv[rt] = v;
        return;
    }
    int m = l + r >> 1;
    if(o <= m) update(o, v, lson);
    else update(o, v, rson);
    push_up(rt);
}
int query(int L, int R, int l, int r, int rt) {
    if(L <= l && r <= R) return maxv[rt];
    int m = l + r >> 1;
    int ret = -INF;
    if(L <= m) ret = max(ret, query(L, R, lson));
    if(R > m) ret = max(ret, query(L, R, rson));
    return ret;
}
  • 区间更新 区间查询
    push_down 在更新或者查询到当前节点的左右儿子节点时，提前更新它的左右儿子节点，
    这就是懒惰操作lazy propagation
    这是一个坎，建议不要去看什么网上的讲解，代码就是最好的讲解，模拟几遍代码就懂了
//以区间更新 区间求和为例
const int N = 1e5 + 10;

#define root 1, n, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1

int sum[N << 2], add[N << 2];

void push_up(int rt) {
    sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}
void push_down(int rt, int m) {
    if(add[rt]) {
        sum[rt << 1] += add[rt] * (m - (m >> 1));
        sum[rt << 1 | 1] += add[rt] * (m >> 1);
        add[rt << 1] += add[rt];
        add[rt << 1 | 1] += add[rt];
        add[rt] = 0;
    }
}
void update(int L, int R, int v, int l, int r, int rt) {
    if(L <= l && r <= R) {
        add[rt] += v;
        sum[rt] += v * (r - l + 1);
        return;
    }
    push_down(rt, r - l + 1);
    int m = l + r >> 1;
    if(L <= m) update(L, R, v, lson);
    if(R > m) update(L, R, v, rson);
    push_up(rt);
}
int query(int L, int R, int l, int r, int rt) {
    if(L <= l && r <= R) return sum[rt];
    push_down(rt, r - l + 1);
    int m = l + r >> 1, ret = 0;
    if(L <= m) ret += query(L, R, lson);
    if(R > m) ret += query(L, R, rson);
    return ret;
}

Ⅲ. 线段树的题目讲解

所有的题目不外乎都是这两种模型，但是题目也有一定的技巧，即使是区间更新也不一定要往下传递lazy标记，
我们将以具体的题目配合进行讲解

1. 单点更新 区间查询

//
//  Created by TaoSama on 2015-05-19
//  Copyright (c) 2015 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>

using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 5e4 + 10;

#define root 1, n, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1

int n, sum[N << 2];

void push_up(int rt) {
    sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}

void build(int l, int r, int rt) {
    if(l == r) {
        scanf("%d", &sum[rt]);
        return;
    }
    int m = l + r >> 1;
    build(lson);
    build(rson);
    push_up(rt);
}

void update(int o, int v, int l, int r, int rt) {
    if(l == r) {
        sum[rt] += v;
        return;
    }
    int m = l + r >> 1;
    if(o <= m) update(o, v, lson);
    else update(o, v, rson);
    push_up(rt);
}

int query(int L, int R, int l, int r, int rt) {
    if(L <= l && r <= R) return sum[rt];
    int m = l + r >> 1;
    int ret = 0;
    if(L <= m) ret += query(L, R, lson);
    if(R > m) ret += query(L, R, rson);
    return ret;
}

int main() {
#ifdef LOCAL
    freopen("in.txt", "r", stdin);
//  freopen("out.txt","w",stdout);
#endif
    ios_base::sync_with_stdio(0);

    int t; scanf("%d", &t);
    int kase = 0;
    while(t--) {
        printf("Case %d:\n", ++kase);
        scanf("%d", &n);
        build(root);
        char op[10]; int x, y;
        while(scanf("%s", op)) {
            if(op[0] == 'E') break;
            scanf("%d%d", &x, &y);
            if(op[0] == 'Q') printf("%d\n", query(x, y, root));
            else if(op[0] == 'A') update(x, y, root);
            else if(op[0] == 'S') update(x, -y, root);
        }
    }
    return 0;
}

//
//  Created by TaoSama on 2015-05-19
//  Copyright (c) 2015 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>

using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 2e5 + 10;

#define root 1, n, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
int n, q, maxv[N << 2];

void push_up(int rt) {
    maxv[rt] = max(maxv[rt << 1], maxv[rt << 1 | 1]);
}

void build(int l, int r, int rt) {
    if(l == r) {
        scanf("%d", &maxv[rt]);
        return;
    }
    int m = l + r >> 1;
    build(lson);
    build(rson);
    push_up(rt);
}

void update(int o, int v, int l, int r, int rt) {
    if(l == r) {
        maxv[rt] = v;
        return;
    }
    int m = l + r >> 1;
    if(o <= m) update(o, v, lson);
    else update(o, v, rson);
    push_up(rt);
}

int query(int L, int R, int l, int r, int rt) {
    if(L <= l && r <= R) return maxv[rt];
    int m = l + r >> 1;
    int ret = -INF;
    if(L <= m) ret = max(ret, query(L, R, lson));
    if(R > m) ret = max(ret, query(L, R, rson));
    return ret;
}

int main() {
#ifdef LOCAL
    freopen("in.txt", "r", stdin);
//  freopen("out.txt","w",stdout);
#endif
    ios_base::sync_with_stdio(0);

    while(scanf("%d%d", &n, &q) == 2) {
        build(root);
        while(q--) {
            char op[2]; int x, y;
            scanf("%s%d%d", op, &x, &y);
            if(op[0] == 'Q') printf("%d\n", query(x, y, root));
            else update(x, y, root);
        }
    }
    return 0;
}

//
//  Created by TaoSama on 2015-05-21
//  Copyright (c) 2015 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>

using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 5e4 + 10;

#define root 1, n, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
int n, q, maxv[N << 2], minv[N << 2];

void push_up(int rt) {
    maxv[rt] = max(maxv[rt << 1], maxv[rt << 1 | 1]);
    minv[rt] = min(minv[rt << 1], minv[rt << 1 | 1]);
}

void build(int l, int r, int rt) {
    if(l == r) {
        int x; scanf("%d", &x);
        maxv[rt] = minv[rt] = x;
        return;
    }
    int m = l + r >> 1;
    build(lson);
    build(rson);
    push_up(rt);
}

int query(int op, int L, int R, int l, int r, int rt) {
    if(L <= l && r <= R) {
        return op ? maxv[rt] : minv[rt];
    }
    int Max = -INF, Min = INF;
    int m = l + r >> 1;
    if(op) {
        if(L <= m) Max = max(Max, query(op, L, R, lson));
        if(R > m) Max = max(Max, query(op, L, R, rson));
    } else {
        if(L <= m) Min = min(Min, query(op, L, R, lson));
        if(R > m) Min = min(Min, query(op, L, R, rson));
    }
    return op ? Max : Min;
}

int main() {
#ifdef LOCAL
    freopen("in.txt", "r", stdin);
//  freopen("out.txt","w",stdout);
#endif
    ios_base::sync_with_stdio(0);

    while(scanf("%d%d", &n, &q) == 2) {
        build(root);
        while(q--) {
            int x, y; scanf("%d%d", &x, &y);
            int Max = query(1, x, y, root);
            int Min = query(0, x, y, root);
            printf("%d\n", Max - Min);
        }
    }
    return 0;
}

2. 区间更新 区间查询

//
//  Created by TaoSama on 2015-05-21
//  Copyright (c) 2015 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>

using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;

#define root 1, n, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
int n, q, sum[N << 2], row[N << 2];

void push_up(int rt) {
    sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}

void push_down(int rt, int m) {
    if(row[rt]) {
        sum[rt << 1] = row[rt] * (m - (m >> 1));
        sum[rt << 1 | 1] = row[rt] * (m >> 1);
        row[rt << 1] = row[rt << 1 | 1] = row[rt];
        row[rt] = 0;
    }
}

void build(int l, int r, int rt) {
    row[rt] = 0;
    if(l == r) {
        sum[rt] = 1;
        return;
    }
    int m = l + r >> 1;
    build(lson);
    build(rson);
    push_up(rt);
}

void update(int L, int R, int v, int l, int r, int rt) {
    if(L <= l && r <= R) {
        sum[rt] = v * (r - l + 1);
        row[rt] = v;
        return;
    }
    push_down(rt, r - l + 1);
    int m = l + r >> 1;
    if(L <= m) update(L, R, v, lson);
    if(R > m) update(L, R, v, rson);
    push_up(rt);
}

int main() {
#ifdef LOCAL
    freopen("in.txt", "r", stdin);
//  freopen("out.txt","w",stdout);
#endif
    ios_base::sync_with_stdio(0);

    int t; scanf("%d", &t);
    int kase = 0;
    while(t--) {
        scanf("%d%d", &n, &q);
        build(root);
        while(q--) {
            int x, y, z; scanf("%d%d%d", &x, &y, &z);
            update(x, y, z, root);
        }
        printf("Case %d: The total value of the hook is %d.\n",
               ++kase, sum[1]);
    }
    return 0;
}

//
//  Created by TaoSama on 2015-05-19
//  Copyright (c) 2015 TaoSama. All rights reserved.
//
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>

using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;

#define root 1, n, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1

typedef long long LL;
int n, q;
LL sum[N << 2], add[N << 2];

void push_up(int rt) {
    sum[rt] = sum[rt << 1] + sum[rt << 1 | 1];
}

void push_down(int rt, int m) {
    if(add[rt]) {
        add[rt << 1] += add[rt];
        add[rt << 1 | 1] += add[rt];
        sum[rt << 1] += add[rt] * (m - (m >> 1));
        sum[rt << 1 | 1] += add[rt] * (m >> 1);
        add[rt] = 0;
    }
}

void build(int l, int r, int rt) {
    add[rt] = 0;
    if(l == r) {
        scanf("%lld", &sum[rt]);
        return;
    }
    int m = l + r >> 1;
    build(lson);
    build(rson);
    push_up(rt);
}

void update(int L, int R, int v, int l, int r, int rt) {
    if(L <= l && r <= R) {
        add[rt] += v;
        sum[rt] += (LL)v * (r - l + 1);
        return;
    }
    push_down(rt, r - l  + 1);
    int m = l + r >> 1;
    if(L <= m) update(L, R, v, lson);
    if(R > m)update(L, R, v, rson);
    push_up(rt);
}

LL query(int L, int R, int l, int r, int rt) {
    if(L <= l && r <= R) return sum[rt];
    push_down(rt, r - l + 1);
    int m = l + r >> 1;
    LL ret = 0;
    if(L <= m) ret += query(L, R, lson);
    if(R > m) ret += query(L, R, rson);
    return ret;
}

int main() {
#ifdef LOCAL
    freopen("in.txt", "r", stdin);
//  freopen("out.txt","w",stdout);
#endif
    ios_base::sync_with_stdio(0);

    while(scanf("%d%d", &n, &q) == 2) {
        build(root);
        while(q--) {
            char op[2]; int x, y, z;
            scanf("%s%d%d", op, &x, &y);
            if(op[0] == 'Q') printf("%lld\n", query(x, y, root));
            else {
                scanf("%d", &z);
                update(x, y, z, root);
            }
        }
    }
    return 0;
}

题解戳这里

题解戳这里

题解戳这里

3. 线段树区间合并

题解戳这里

题解戳这里

题解戳这里

4. dfs序维护区间线段树

题解戳这里

5. 扫描线与线段树

  • HDU 1542 Atlantis
    矩形面积并 不用传递懒惰标记 模拟一下就懂了
    update:区间更新

  • POJ 1177 Picture
    矩形周长并 与上面那个题相似 两种做法
    第一种直接横着扫描一次再竖着扫描一次
    第二种在横着扫描的时候再同时维护 竖线的个数
    update:单点增减 query:区间求和

  • HDU 1255 覆盖的面积
    前面的与矩形面积并类似, 不同的是push_up的时候要考虑至少覆盖一次one和至少覆盖两次two的更新
    update:区间更新

扫描线与线段树经典三题，全部详细题解戳这里

6. 线段树求第K大(其实就是在线段树上二分)

题解戳这里

题解戳这里

7. 高维线段树与多颗线段树

题解戳这里

题解戳这里

8. 线段树维护信息举例

题解戳这里

题解戳这里
TaoSama
关注
  • 0
    点赞
  • 踩
  • 3
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
线段树建树
12-14
线段树是一种二叉树，也就是说，每个线段都可以用一二叉树表示 比如一个长度为4的线段可以如此表示： ——————————————-4 1————-2————-3————4 1 2 3 4 如果你要表示线段上的和，最上面的根...
线段树
qq_47783181的博客
12-03 359
线段树 线段树是什么？ 线段树是一颗二叉搜索树，对于一个线段，用二叉树的形式表示。它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。 线段树的作用 用来解决区间问题 最基本的用来单点修改，区间修改，单点查询，区间查询。 其中两个经典问题是维护某段长度的最大值最小值，某段区间和。 然后可以引申出求区间最大值和最小值之差。 线段树的操作 线段树有五个操作，pushup，pushdown，build，query，modify pushup 操作 这个操作的意思就是向上维护，如果修改了某一点或
22/5/2
aidaqiudeaichao的博客
05-02 232
1，cf Game with Chips；2，acwing 243.一个简单的整数问题2（线段树）；3，亚特兰蒂斯（扫描线）；4，维护序列； 题意：给你n x m的棋盘，有k个芯片分布在棋盘上，操作是左右上下各平移一格，要求第i个芯片至少经过一次给定位置；芯片遇到墙后，若仍往墙的方向走，则会不动；多个芯片可以在同一格； 操作次数不超过2nm次； 输出操作序列和操作步数；没有序列输出-1； 思路：直接将所有的芯片先移动到（1，1）在带着整体一个个走，遍历一遍棋盘，必能完成要求； 而且不会超过2nm；
【算法】线段树
weixin_63896439的博客
05-02 222
第二次修改[5, 8]不能覆盖结点5，需要再向下搜到结点11:[5, 5]，从而破坏了tag[5]，此时原tag[5]记录的区间统一修改就不得不往它的子结点传递和执行了，传递后tag[5]失去了用途，需要清空。区间[L, R]是需要更新的区间。（1）左子树递归到结点5，即区间[4, 5]，完全包含在[4, 9]内，打标记tag[5] = 3，更新tree[5]为20，不再继续深入；（3）右子树递归到结点6，即区间[6, 8]，完全包含在[4, 9]内，打标记tag[6]=3，更新tree[6]为23。
【线段树】模板题pushup+pushdown操作
行码棋
09-20 1196
线段树pushup和pushdown操作的经典模板
最大数(线段树pushup操作)
名字不能相同
08-13 202
#include <iostream> #include <cstdio> using namespace std; const int N = 200007; int m, p; struct Node { int l, r; int v; }tr[N * 4]; void pushup(int u) { tr[u].v = max(tr[u<<1].v, tr[u<<1|1].v); } void build(int u, int l,
线段树模板
02-03
线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。 使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的...
线段树解题报告
01-03
思路：树状数组维护，类似于树状数组求逆序对+思维（思维量很小） #include using namespace std; const int N = 2e5+9; typedef long long ll; struct node{ ll a,b; friend bool operator <(node a,node b){ ...
线段树_线段树_
10-01
线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的...
C语言线段树讲解
06-15
C语言线段树讲解，C语言线段树讲解课件，C语言线段树讲解PPT
线段树 go语言实现
09-18
go语言实现的线段树源码, 可以直接运行, 代码简洁清晰, 快去下载吧
线段树讲义PPT
12-05
线段树，类似区间树，它在各个节点保存一条线段（数组中的一段子数组），主要用于高效解决连续区间的动态查询问题，由于二叉结构的特性，它基本能保持每个操作的复杂度为O(logn)。
细讲线段树
12-04
这PPT讲了线段树的结构、性质、存储、修改、查询操作，适合新手看。
c++线段树例题亚特兰蒂斯
07-06
有几个古希腊书籍中包含了对传说中的亚特兰蒂斯岛的描述。 其中一些甚至包括岛屿部分地图。 但不幸的是，这些地图描述了亚特兰蒂斯的不同区域。 您的朋友 Bill 必须知道地图的总面积。...你自告奋勇写了一个计算这个...
C语言算法题-线段树
08-09
Alice和Bob又在挑战智力，这次的模式是这样的，Alice写下若干个数给Bob，之后会发出若干指令，让Bob给某数加上一个数（A），或者给某数减去一个数（S），或者查询某两个数之间所有数字之和（Q），有时他们也身份互换...
【树】一步一步写线段树（三）——实战演练（二）PushUp的应用
IDDFS
02-24 572
查询最小值与修改一个值 题目：RMQ问题再临-线段树【HihoCoder-1077】 描述 上回说到：小Hi给小Ho出了这样一道问题：假设整个货架上从左到右摆放了NNN种商品，并且依次标号为1到NNN，每次小Hi都给出一段区间[L,R][L,R][L,R]，小Ho要做的是选出标号在这个区间内的所有商品重量最轻的一种，并且告诉小Hi这个商品的重量。但是在这个过程中，可能会因为其他人的各...
【hdu3308 LCIS】【线段树】【pushup】【最长连续上升序列】
running_acmer的博客
10-16 450
【链接】 http://acm.hdu.edu.cn/showproblem.php?pid=3308 【题意】 给你n个数，m个操作。 操作有两种： 1.U x y 将数组第x位变为y   2. Q x y 问数组第x位到第y位连续最长子序列的长度 【思路】 满足区间可加。 线段树维护信息：区间最长连续上升序列，前缀最长上升序列，后缀最长上升序列。 pushup(p)修改的时...
HDU 3308 LCIS 线段树 PushUp应用
Katapeltes
11-13 394
http://acm.hdu.edu.cn/showproblem.php?pid=3308#include<bits/stdc++.h> using namespace std; const int MAX=100005; int N,M,A[MAX];struct Node { int l,r,c; //l,r - 左右边界 c - 长度 int ln,rn;
线段树详解 （原理，实现与应用）
热门推荐
岩之痕
09-09 13万+
线段树详解 By 岩之痕 一：综述 线段树是一种可以快速进行区间修改和区间查询的数据结构。点修改，区间修改和区间查询的复杂度都是O(log2(n)) 并且，线段树可以维护很多种类的信息。说到线段树就不得不提一下树状数组，树状数组维护的信息必须满足区间减法，因为树状数组只是维护1到X的信息，通过相减来得到区间信息，代码简单而且速度快，占用空间又少于线段树，所以一般情况下可以用树状数组的地方就
Python 线段树
最新发布
10-06
Python中的线段树是一种用于解决区间查询问题的数据结构。线段树可以被看作是一棵二叉树，其中每个节点代表了一个区间。每个内部节点都有两个子节点，左子节点代表区间的左半部分，右子节点代表区间的右半部分。叶...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值