归一化问题

使用matlab学习svm，发现在对数据进行预处理时，要对数据进行归一化，并且，遇到问题：训练数据和测试数据是一起归一化处理好还是分开归一化处理好？怎么确定归一化的范围多大？是[0,1]还是[-1,4]等，为什么归一化范围不同，对分类精度有影响？
断断续续的在网上找了几天，和同学讨论了一下，总想找个确凿的答案，但是总结来说为：
1、大多数情况应该对数据进行归一化处理，特别是在特征范围相差较大情况下。实在不知道归一化处理好不好时，那就针对自己的数据多进行实验测试一下。
2、对于训练数据和测试数据是否需要一起归一化的问题，认为多数情况下一起归一化处理获得的分类精度更好。
3、归一化范围，一般都取[-1，1]，[0,1]，并且前者效果好一些。
问题一： 对于归一化处理，其实现的是将一组数据映射到特定的数值范围内。比如matlab自带的mapmaxmin函数，所用的映射函数为y=(ymax-ymin)*(x-xmin)/(xmax-xmin)+ymin 其中，x为输入，y为归一化处理后的输出，[ymin,ymax]是映射的范围，如[0,1]或者[-1,4]等，而（xmax,xin）是输入的数据集x的最小值和最大值。如对于一个178*13的数据集，每一行代表一瓶酒，每一列代表一种特征（如下图）一共13个特征。而在这组数据中，特征5和特征13相对于其他数据，是两组奇异样本数据，所谓奇异样本，是相对于其他输入样本特别大或特别小的样本矢量。

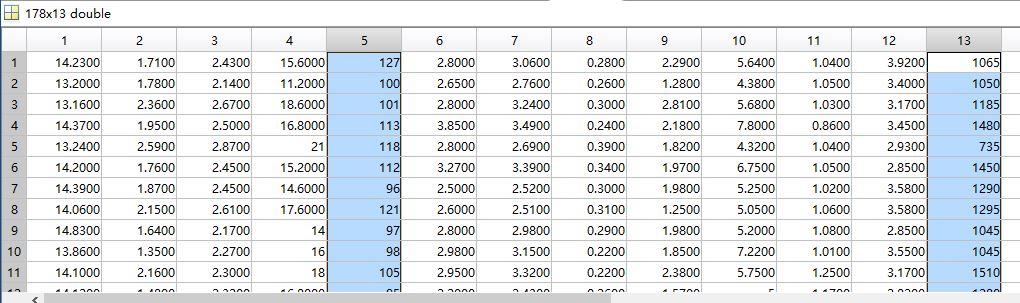
在对数据进行操作前，先将数据归一化处理，使其无量纲化，避免较大数值的数据的变化掩盖掉小数值的变化。比如是二维数据，特征1的取值范围是[1000,2000],特征2的取之范围是[1,2],那么我们二维画出的这些数据点基本都是在一个长条的数据区域内（1*1000的数据区域内），此时如果进行分类，特征2的变化几乎何以被忽略掉。同时这种分布不平衡的数据还会引起训练时间长，大数值样本或是收敛受到影响等问题。
mapmaxmin函数对特征数据归一化处理，是对每一特征来单独归一化的，也就是对图中每一列数据进行归一化。下图是归一化后的数据。归一化后的数据都被映射在[-1,1]范围内，对进一步的数据操作提供方便。

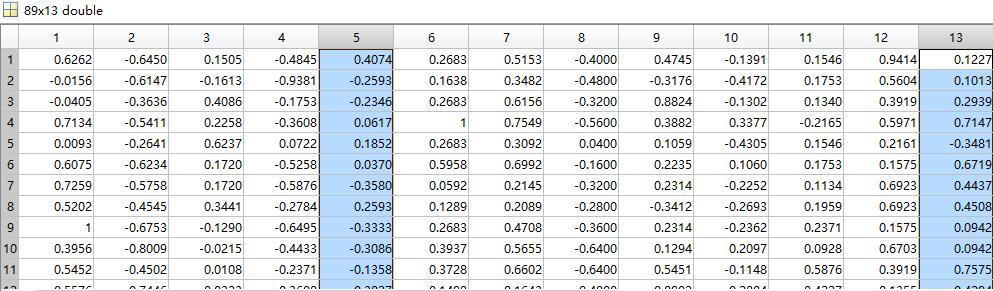
问题二：在分类问题中，训练数据和测试数据是否需要一起归一化处理，没有一个固定的答案说怎样好怎样不好，但是，一起进行归一化处理，我们可以想到，这种做法会将训练数据和测试数据看作一个整体，因为此时映射函数中的输入数据集是训练数据和测试数据的总和，里面的（xmax,xmin）也是这个总和中的最大值和最小值，实际上，将训练数据和测试数据一起归一化，测试数据在一定程度上影响着分类模型的训练。此后再运用此分类模型对测试数据进行分类，避免产生”相同的训练数据和测试数据，因为训练数据集和测试数据集的（xmax,xmin）不同，在分别归一化后，相同的数据获得不同的归一化值，被分在不同的类“的情况。但是，具体哪种归一化做法可以获得更好的分类效果，只能根据自己的数据集，进行实验。

问题三：归一化可以将数据集中太大或太小的样本映射到统一的范围内，但是，这个范围区间的选择怎么定呢？理论上，这个值可以自己随便设定，但是一般情况下，选取[-1,1]，2个数值长度的空间，能得到比较好的分类效果。下面是测试实验截图：
（1）采用训练数据和测试数据一起归一化处理，范围为[0,1],获得精度为61.79%

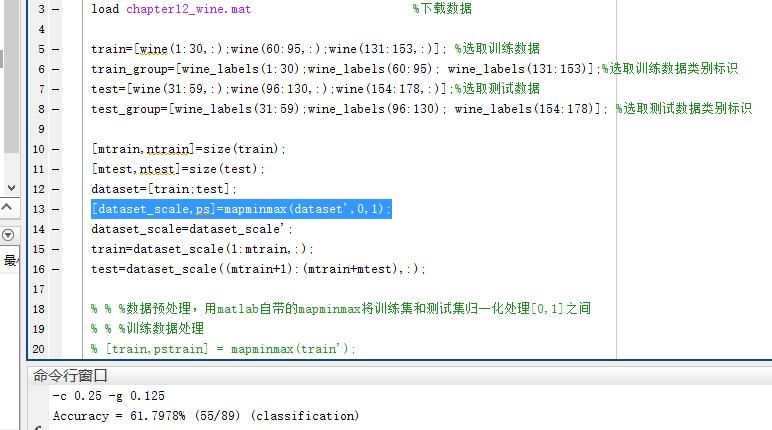
(2)采用训练数据和测试数据一起归一化处理，范围为[-1,1],获得精度为98.87%

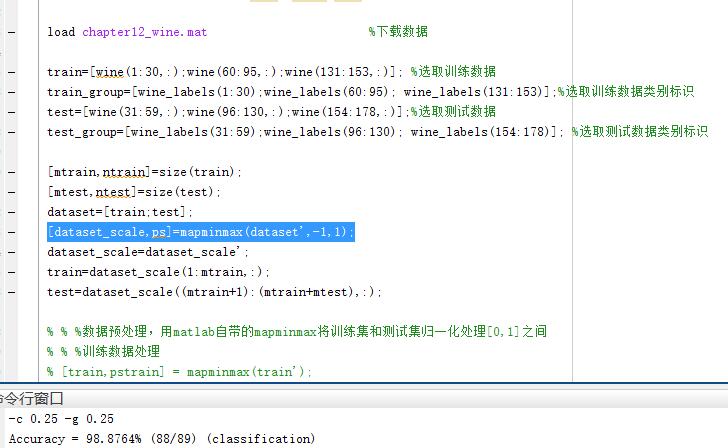
对于归一化范围，我认为重要的不是选择[0,1]还是[-1,1]，而是这个区间的长度是多少，这个区间长度才是对分类精度影响的真正原因。对于[0,1]或者是[3,4]等，归一化区间长度是1，实验验证他们的分类精度都是相同的61.79%，长度为2的[-1,1]和[3,5]归一化范围获得的分类精度都是98.87%，在我的理解，这个长度，直接影响着的是数据集的分布稀疏程度，而对于某些高维大数据集合的分类来说，如果没有稀疏性，可能svm并不实用。但是这个归一化区间长度并不是越大越好，试验中，将范围设置为[-1,10],分类精度只有65.16%，归一化范围过大，又会丧失了归一化的优势。