Matrix的使用范围非常广泛,我们平时使用的Tween Animation,其在进行位移、缩放、旋转时,都是通过Matrix来实现的。除此之外,在进行图像变换操作时,Matrix也是最佳选择。
Matrix是一个3*3的矩阵,如图所示:
我们可以直接通过Matrix.getValues方法获取Matrix的矩阵值(浮点型数组类型),然后修改矩阵值(Matrix类为每一个矩阵值提供了固定索引,如:MSCALE_X、MSKEW_X等),最后通过Matrix.setValues方法重新设置Matrix值,已达到修改Matrix的目的。这种方式要求我们对Matrix每一个值的作用都要十分了解,操作起来比较繁琐,但却是最灵活、最彻底的操作方式。
具体要修改哪些Matrix值,则取决于要实现什么效果,从本质上这是一个数学问题,这里给出几种比较常见的方案:
-
实现Translate操作
位移操作在Matrix中对应是MTRANS_X和MTRANS_Y值,分别表示X和Y轴上的位移量,假设在X和Y轴上分别位移100px,那么对应的Matrix就是

2.实现Scale操作
缩放操作在Matrix中对应的是MSCALE_X和MSCALE_Y值,分别表示X和Y轴上的缩放比例,假设在X和Y轴上分别放大2倍,那么对应的Matrix就是
3.实现Rotate操作
旋转操作在Matrix中对应是MSCALE_X、MSCALE_Y、MSKEW_X和MSKEW_Y值,假设我们要以坐标原点为中心,旋转A度,那么对应的Matrix就是
4.实现Skew操作
错切操作在Matrix中对应的是MSKEW_X和MSKEW_Y,分别表示X和Y轴上的错切系数,假设在X轴上错切系数为0.5,Y轴上为2,那么对应的Matrix就是
其他3种操作都比较常见,但是错切操作我们可能不是很熟悉。
错切可分为水平错切和垂直错切。
水平错切表示变换后,Y坐标不变,X坐标则按比例发生平移,且平移的大小和Y坐标成正比,即新的坐标为(X+Matrix[MSKEW_X] * Y,Y)。
垂直错切表示变换后,X坐标不变,Y坐标则按比例发生平移,且平移的大小和X坐标成正比,即新的坐标为(X,Y+Matrix[MSKEW_Y] * X)。
当然,我们也可以同时实现水平错切和垂直错切。
关于为什么修改Matrix的这些值后,就实现了位移、缩放、旋转和错切操作,就主要是数学推导过程了,可以参考这篇文章—— Android中图像变换Matrix的原理,讲解的非常详细,强烈推荐。
除了可以直接修改Matrix值,Matrix类还提供了一些API来操作Matrix。这里主要介绍几类比较常用的API。
setXXX、preXXX和postXXX
XXX可以是Translate、Rotate、Scale、Skew和Concat(表示直接操作Matrix矩阵)。我们主要搞清楚这3种API的区别就OK了。
setXXX,首先会将该Matrix设置为单位矩阵,即相当于调用reset()方法,然后再设置该Matrix的值。preXXX,不会重置Matrix,而是被当前Matrix左乘(矩阵运算中,A左乘B等于A B),即M’ = M S(XXX)。postXXX,不会重置Matrix,而是被当前Matrix右乘(矩阵运算中,A右乘B等于B A),即M’ = S(XXX) M。
当这些API同时使用时,又会出现什么效果那,我们来看个例子:
1 2 3 4 5 6 7 8 9 | Matrix matrix = new Matrix(); float[] points = new float[] { 10.0f, 10.0f }; matrix.postScale(2.0f, 3.0f);// 第1步 matrix.preRotate(90);// 第2步 matrix.setScale(2f, 3f);// 第3步 matrix.preTranslate(8.0f, 7.0f);// 第5步 matrix.postTranslate(18.0f, 17.0f);// 第4步 matrix.mapPoints(points); Log.i("test", points[0] + " : " + points[1]); |
最后得到的结果是:54.0 : 68.0
可以发现,在第3步setScale之前的第1、2步根本就没有用,直接被第3步setScale覆盖了。所以最终的矩阵运算为
Translate(18,17) * Scale(2,3) * Translate(8,7) * (10,10)
这样,就很容易得出最后的结果了。
这里也许会有一个疑问,为什么坐标点(10,10)会被结果矩阵(矩阵运算虽然不满足交换律,但是满足结合律)左乘,而不是右乘。这一点我们看一下下面的矩阵运算就会明白。
等号左边是变换后的坐标点,等号右边是Matrix矩阵左乘原始坐标点。因为Matrix是3行3列,坐标点是3行1列,所以正好可以相乘,但如果反过来,就不满足矩阵相乘的条件了(
左边矩阵的列数等于右边矩阵的行数
)。所以,就可以理解为什么是结果矩阵左乘原始坐标点了。
等号左边是变换后的坐标点,等号右边是Matrix矩阵左乘原始坐标点。因为Matrix是3行3列,坐标点是3行1列,所以正好可以相乘,但如果反过来,就不满足矩阵相乘的条件了(左边矩阵的列数等于右边矩阵的行数)。所以,就可以理解为什么是结果矩阵左乘原始坐标点了。
也正因为这一点以及矩阵的结合律,所以我们可以理解上面矩阵运算的流程:
先对原始坐标点(10,10)进行Translate(8,7)位移,然后再对中间坐标点(18,17)进行Scale(2,3)放大,最后再次对中间坐标点(36,51)进行Translate(18,17)操作,就得到了最后的坐标点(54,68)。
这里还有一个小Tips:
当需要对Matrix矩阵进行比较复杂的设置时,可以把这些复杂的设置,拆分为多个步骤,每一个步骤都是一个简单的Matrix,然后再依据这些步骤的先后顺序,决定是通过左乘 or 右乘得到结果矩阵,最后通过结果矩阵左乘原始坐标就OK了(设计时,可以拆分之后理解,但最终运算时还是要得到一个结果矩阵,再去操作原始坐标)。
mapPoints mapRect mapVectors
这些API很简单,主要是根据当前Matrix矩阵对点、矩形区域和向量进行变换,以得到变换后的点、矩形区域和向量。经常和下面的invert方法结合使用。
invert
通过上面的mapXXX方法,可以获取变换后的坐标或者矩形。但假设我们知道了变换后的坐标,如何计算Matrix变换前的坐标那?!
此时通过invert方法获取的逆矩阵就派上用场了。所谓逆矩阵,就是Matrix旋转了30度,逆Matrix就反向旋转30度,Matrix放大n倍,逆Matrix就缩小n倍。假设逆矩阵是invertMatrix,那么Matrix.preConcat(invertMatrix) 和 Matrix.postConcat(invertMatrix) 都应该等于单位矩阵(但实际上会有一些误差)。
所以,通过Matrix和invertMatrix对坐标进行变换的规则可总结如下:

逆矩阵在进行自定义View Touch事件处理时很有用,假设我们在自定义View中,通过Matrix(包含了旋转、缩放和位移操作)绘制了Bitmap,现在想要判断Touch事件是否在变换后的Bitmap范围内,应该如何操作那?!
首先想到的可能是下面的方案:
1 2 3 4 | RectF rect = new RectF(bitmap.getWidth(),bitmap.getHeight()); //假设matrix就是对bitmap进行变换的矩阵 matrix.mapRect(rect); boolean isTouchBitmap = rect.contains(touchX,touchY); |
但是这种方式实际上不是非常的准确,通过matrix变换后的矩形区域并不是真实的Bitmap区域,而是包含bitmap的矩形区域(很难描述啊),看下图就知道了:

图中的绿色矩形区域就是我们进行判断的rect区域,很明显误差很大哈。既然正向操作不可行,那就只能试下逆向操作了:
1 2 3 4 5 | RectF rect = new RectF(bitmap.getWidth(),bitmap.getHeight()); float eventFloat[] = new float[]{touchX,touchY}; //假设invertMatrix是matrix的逆矩阵,这里对Touch坐标进行逆向操作。 invertMatrix.mapPoints(eventFloat); boolean isTouchBitmap = rect.contains(eventFloat[0],eventFloat[1]); |
通过这种方式,首先会对Touch坐标进行逆矩阵操作,然后再判断是否落在原始bitmap矩形区域内(上图中的小企鹅),就比较精确了。精妙哈!!!
Canvas.getMatrix的坑
通过Canvas获取Matrix矩阵的拷贝,从API16开始,不再推荐使用。至于原因,可参考Google的解释Issue 24517: Canvas getMatrix/setMatrix with hardware acceleration bug,里面提供了示例代码。
主要原因是,在开启硬件加速的情况下,Canvas.getMatrix 获取的矩阵是相对于Canvas所属View的,而Canvas.setMatrix 则会把所设置的矩阵当做相对于整个屏幕(包括系统栏)。
所谓相对于某个View,就是说不管这个View在屏幕中的任何位置,通过这个View的Canvas获取的Matrix的X和Y位移都是0,也就是Matrix在当前View的本地坐标系中,和View的left和top值无关。
所谓相对于整个屏幕,也就很好理解了,即获取的Matrix是在整个屏幕表示的世界坐标系中的,一般情况下,获取的矩阵的X位移为view.left值,Y位移为系统栏的高度 + view.top值。并且后续对Canvas的变换操作都是基于这个初始矩阵进行的。
所以在硬件加速的情况下,调用canvas.setMatrix(canvas.getMatrix())后,就会导致View默认从屏幕左上角(包含了系统栏)开始绘制,这样就会有一部分内容被系统栏遮挡住。
这里对Google提供的示例代码进行了简化,就是把一个自定义View添加到带有系统栏的Activity中,自定义View的onDraw方法如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | protected void onDraw(Canvas canvas) { canvas.save(Canvas.MATRIX_SAVE_FLAG); Matrix matrix = canvas.getMatrix(); //查看获取的初始Matrix Log.i("matrix",matrix.toString()); // This line changes the canvas' transformation when hardware acceleration is turned on (but shouldn't) canvas.setMatrix(matrix); mPaint.setColor(Color.GREEN); //draw一个200*200的矩形区域 canvas.drawRect(0, 0, 200, 200, mPaint); canvas.restore(); // here the bottom right corner of the green rectangle should lie(but doesn't) mPaint.setColor(Color.RED); canvas.drawPoint(210, 210, mPaint); } |
在没有开启硬件加速的情况下,矩形区域和红点显示正常,
Canvas.getMatrix方法获取的Matrix也是在屏幕世界坐标系中的,即Matrix{[1.0, 0.0, 0.0][0.0, 1.0, 60.0][0.0, 0.0, 1.0]},其中Y轴位移为60,表示的就是状态栏的高度。这样重新setMatrix之后,就不会出现问题,如图所示:
但是在开启硬件加速的情况下,矩形区域有一部分被系统栏遮挡住了,可以对比下红点的位置就就知道了,同时获取的Matrix也是相对于当前View本地坐标系的,即Matrix{[1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]},没有产生任何位移。这样重新setMatrix之后,就会出现问题(因为对Matrix的理解不同),如图所示:
既然,Canvas.getMatrix被废弃了,那有什么替换的方法嘛?!这里Google并没有明确的指出。但是我觉得有两种方式可以实现类似功能。
- 不获取Matrix,直接通过Canvas提供的位移、旋转、缩放等API来实现类似功能。
- 从API11开始,提供了View Properties,可以直接对View进行位移、旋转、缩放等操作,同时也提供了
View.getMatrix方法来获取当前View的Matrix(也算是Canvas.getMatrix的替代方案了)。当然,这个Matrix也是相对于View本身本地坐标系的。
本文简单介绍了Matrix的基本使用方法,关于Matrix的底层原理,还没有涉猎,后续深入研究后,再补充进来。
最后推荐几篇比较好的Matrix相关的文章。
- Android中图像变换Matrix的原理、代码验证和应用(一)
- Android中图像变换Matrix的原理、代码验证和应用(二)
- Android中图像变换Matrix的原理、代码验证和应用(三)
- 深入理解 Android 中的 Matrix









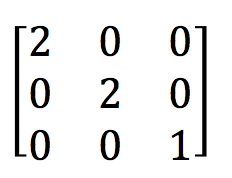



















 9629
9629

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








