本文介绍了机器学习的基本概念，包括吴恩达在Stanford课程中对机器学习的定义，以及监督学习和无监督学习的区别。接着详细探讨了线性回归模型，包括单变量线性回归的假设函数、代价函数和梯度下降法。通过梯度下降算法，找到使代价函数最小化的参数，以实现模型的优化。强调了学习速率在梯度下降过程中的重要性，以及其对收敛速度和局部最优解的影响。
刚开启机器学习之路，今天来整理一下，我在week1&week2学到了什么！
一：机器学习概述
（1）什么是机器学习？
在Stanford的课程上，吴大神说机器学习的定义有两种：
a:机器学习是关于一个领域的学习，不是通过显示地编程手段给计算机一种能力去学习！
Machine leaning :Field of study that gives computers the ability to learn without being explicitly programmed
b.假设用P来评估计算机程序在某个任务类T上的性能，若一个程序通过利用经验E在T的任务上获得了性能改善，则我们就说关于T和P，该程序对E进行 了学习！
A conputer program is said to learn from experience E with respect to some task T and some performance measure P,if its performance on T ,as measured by P,impoves with experience E.
（或者说一个程序被认为能从经验E中学习，解决任务T，达到性能度量值P，当且仅当，有了经验E，经过P评判，程序在处理T时的性能有所提升。）
E.g：在玩下棋游戏的时候，E表示多次下棋的经验，T表示下棋的任务，P表示赢得下次下棋游戏的概率。
(2)机器学习算法：
监督学习和无监督学习，还有一些其他，加强学习和推荐系统！
A：监督学习-Supervised Learning
监督学习是指我们给定一个数据集，这个数据集上已经知道确定的正确的答案，即right answer，也就是认为输入和输出之间存在一种关系；
在房价的例子中，我们给了一系列的房子的数据，我们给定数据集中每个样本的正确价格，即他们实际的售价然后运用学习算法，算出更多的正确的答案。
监督学习又分成：
a:回归-regression：我们希望预测的结果是连续的值，例如房价问题，预测房价是回归问题，（一般我们会认为房价是一系列的离散的值，但是我们通常又把房价看成实数，看成标量，所以又把它看成连续的数值），但是相对的我们给定一个价格，问是否卖出去的价格多余或者小于这个给定价格，这个是一个分类问题！
b:分类-classification我们希望预测的结果是一个离散的值，例如明天下不下雨问题，或者预测肿瘤是良性还是恶性的，就是0和1的输出结果！（但是需要注意的是，分类输出的结果可能不止两个值，假设可能存在三种乳腺癌的，我们会希望输出0,1,2，3，那么0表示的是良性，1表示的是第一类乳腺癌，2表示第二类乳腺癌，3表示第三类乳腺癌，这也算是一种分类问题。）
B：无监督学习-Unsupervised Learning
无监督学习所有的数据都是一样的，没有标记label（无标签），没有给出正确的答案，允许我们解决这个问题，但是无需知道结果是什么样，在预测结果上是没有反馈的！
聚类算法：基因组，自动将相似的基因分成组；还有Google的新闻把关于一个论点（枪杀案或者泄露油）的所有新闻放在一起；朋友圈；市场分区；
无聚类：在嘈杂的环境下，区别出各种声音
二：线性回归模型
A.单变量线性回归（linear regression with one variable）
（1）基本概念：
在监督学习中，我们有一个训练集training set
m:训练集的样本的数目；
x's:输入变量或者特征值；
y's:输出变量或者目标变量；
：表示第i个训练样本。
（2）假设函数（hypothesis function）
例如房价问题，我们考虑最简单的线性回归问题，我们把假设函数设置成：，只有一个特征值或者说输入变量，把我们的训练集传输给学习算法，然后等系统学习了以后，得到一个假设函数h，最后比如房价问题，你输入你的房子的大小，得到房价。假设我们存在四个点，分别是（1,1）,(2,2),(3,3),(4,4),这样我可以很轻松的找到一个直线，h（x）=x；但是我可以案例不是这么简单的，那考虑如何选择两个未知参数呢，这时候需要考虑代价函数了，代价函数就是我对于所有的样例，做出的预测的结果与真实结果之间的差值的平方的均值，找到两个参数使得这个cost function结果最小！
（3）代价函数（cost function）
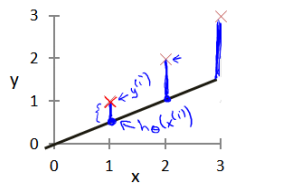
我们现在要做的就是为我们的模型选择合适的参数和
，我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度，模型所预测的值与训练集中实际值之间的差距就是建模误差（modeling error）。（蓝色的线就是误差）
我们的目标就是选择出可以使得建模误差平方和最小的建模参数，即使得代价函数
（4）梯度下降法（Gradient descent）——用来求函数最小值的算法
目的：找到满足使得J取最小值的和
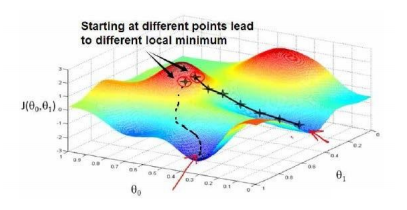
思想：开始时我们随机的选择一个参数的组合（,
,.....,
）,计算代价函数，然后寻找 下一个能让代价函数值下降最多的组合。我们持续这么做直到到一个局部最小值（local minimum），因为我们没有尝试完所有的参数组合，所以我们不能确定得到的局部最小值是否是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。
就拿NG在视频中所说的方法，假设你站在山上的一点，在梯度下降算法中，我们要做的就是旋转360度，看看朝着哪个方向能够最快的下山，如何你迈出一小步，然后再看看，在迈出一小步，重复上面的步骤，从这个新的点，你环顾四周，并决定从什么方向上你能够最快的下山，码处一小步，以此类推，直到你接近局部最低点的位置。
批量梯度下降（batch gradient descent）算法的公式：
注意梯度下降法必须实现的是，同时的更新参数和
，下面放图，实在不好手打。。。。
repeat until convergence{
}
上述公式其中的是学习率（learning rate），他决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数
在这个更新过程中，需要注意的是我们需要同时更新所有的参数，，而不是一个一个依次进行，
例如两个参数和
的情况：下面是正确的更新过程
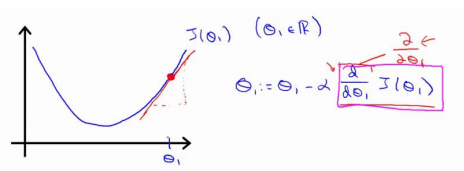
总结：梯度下降算法就是通过对theta的赋值使得J(θ)按梯度下降最快的方向进行，一直迭代下去，最终得到局部最小值，其中α是学习速率，他决定了我们沿着使得代价函数下降程度最大的方向向下迈出的步子有多大！
上图你会发现该点的求导是一个正斜率，即求导结果是正数，那么与α相乘在减去之后，θ会变小，即会往左边走，如果α足够小，一点一点的会挪到最小值点
若是学习速率a很大，会导致一个什么现象呢？
a过大的时候，梯度下降会错过最小值点，很难是收敛，甚至会发散；结合下图解释，如果你在左侧，你对j求导之后，由于切线的k是负数，所以你的θ会变大，向x正方向走，如果a太大了，直接overshoot the minimum，错过最小值点；之后你在对这点求导，发现切线的斜率是正数，θ会减小，但是a过大，可能就过了，往复下去可能会越来越发散。。
若是学习速率a很小，又会出现什么现象呢？
但是a很小呢，也存在不好的，那就是梯度下降过程特别的慢；
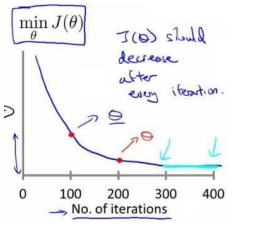
综上可知梯度下降关键在于选择合适的learning rate，只有选择了合适的a之后，我们不断的同时更新theta，然后知道theta不在变化，或者说cost function的偏导数部分为0，
如果说我的cost function到达了局部最优的地方，那就不会在变化了！（注意局部最优和全局最优！）
注意：梯度下降不一定能够找到全局最优解，但是很可能是一个局部最优解，若cost function是一个凸函数，那么我们一定能够找到一个全局最优解，你可以把cost function看成是碗状的，梯度下降类似于下山问题，那样很容易就找到了！
梯度下降算法并不仅仅试用于线性回归，可以用来最小化所有代价函数！
for every j
，参见下图：
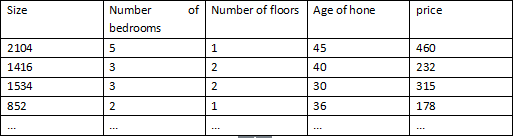
:第i个训练实例，是特征矩阵中的第i行，是一个向量（vector）
：表示特征矩阵第i行第j个特征，也就是第i个训练实例的第j个特征
，则公式变成：
上面的公式可以表示成,（T表示矩阵的转置）这个表达式只针对我们一个训练实例的输出结果，一般在我们书写代码的时候，书写成：，这样得到的结果是一个m维的向量，每一行对应一个实例的输出结果，而根据矩阵运算的法则，我们可以推导出这个公式，但是根据你得到的X和θ的维度有关，具体情况具体分析！
for j=0,1,2,...n)
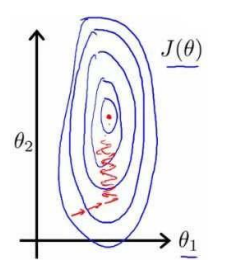
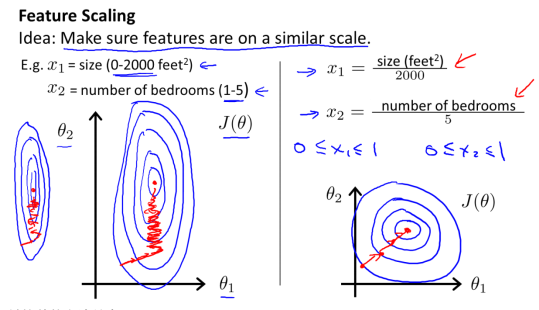
:其中
是平均值，
是标准差
或者三次方模型
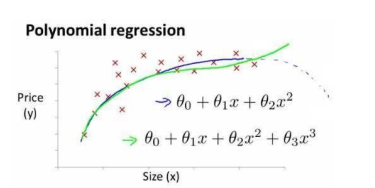
,将模型转化成线性回归模型！
∈R,那么我们可以得到代价函数是一个二次函数，假设
,那么我们对J求导，即
，求得使得J最小的θ值
，
,那么我们使得
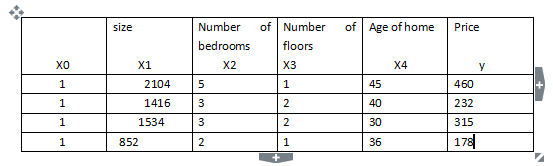
），并且我们的训练集结果为向量y，则利用正则方程解出向量
，这个公式的推导实在难打!!
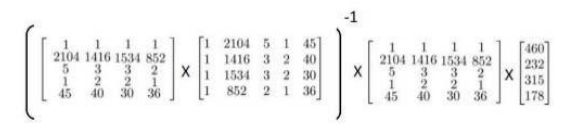
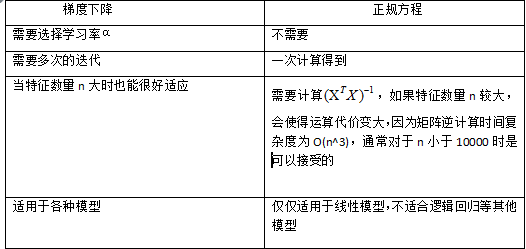
可能存在不可逆的情况，比如说上面我们所说的房价问题的两个相关的尺寸，以及m<=n的情况！
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
