GAN中的散度和距离

KL散度（相对熵）

可以用来衡量两个概率分布之间的差异，又称为相对熵，和信息熵。
概率分布P1和P2的KL散度：
$$KL(P1||P2)=E_{xp1}log(\frac{p1}{p2})={\int }_{x}p1(x)log(\frac{p1(x)}{p2(x)})dx$$

特点: 非负性，非对称，不是距离（不满足距离定义的条件 三角不等式）
缺点：不是对称的，有时用它来训练神经网络会有顺序不同造成不一样的训练结果的情况（训练时间差异的问题）。为了克服这个问题，有人提出了新的衡量公式JS散度。

JS散度：

JS 散度 ：相似度衡量指标。现有2个分布P1和P2，其JS 散度公式为：
$$JS(P1||P2)=\frac{1}{2}KL(P1||\frac{P1+P2}{2})+\frac{1}{2}KL(P2||\frac{P1+P2}{2}))$$
JS 散度是对称的，而且因为是两个KL 叠加，由于KL的值一定大于等于0，所以JS散度也一定大于等于0.

特点：取值范围0-1，对称的， 两个分布P,Q距离远 完全重叠时KL散度无意义，而JS散度是一个常数（即此时梯度消失）。

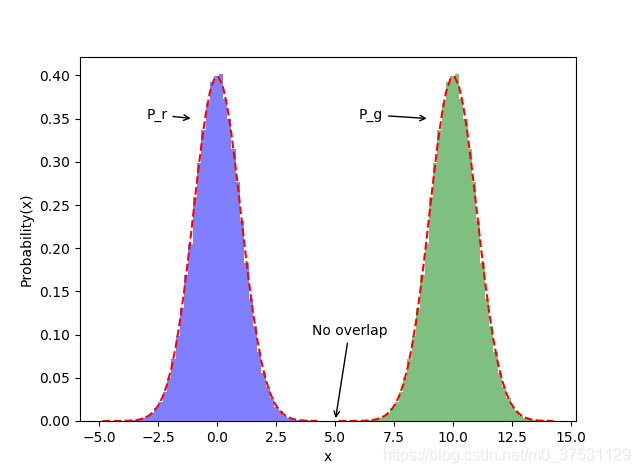
GAN中提到的当2个分布完全不重叠的时候JS散度是一个固定值log2， 这个值是怎么来的呢？

我们根据下图来计算一下：
$$\begin{gathered} JS(P||Q)=\frac{1}{2}KL(P||\frac{P+Q}{2}))+\frac{1}{2}KL(Q||\frac{P+Q}{2})) \\ =\frac{1}{2}\sum p(x)log\frac{p(x)}{(p(x)+q(x))/2}+\frac{1}{2}\sum q(x)log\frac{q(x)}{(p(x)+q(x))/2} \\ =\frac{1}{2}\sum p(x)log\frac{2p(x)}{p(x)+q(x)}+\frac{1}{2}\sum q(x)log\frac{2q(x)}{p(x)+q(x)} \\ =\frac{1}{2}log2+\frac{1}{2}\sum p(x)log\frac{p(x)}{p(x)+q(x)}+\frac{1}{2}log2+\frac{1}{2}\sum q(x)log\frac{q(x)}{p(x)+q(x)} \\ =log2+\frac{1}{2}\sum p(x)log\frac{p(x)}{p(x)+q(x)}+\frac{1}{2}\sum q(x)log\frac{q(x)}{p(x)+q(x)} \end{gathered}$$
注意 因为 $\sum p(x)=\sum q(x)=1$ 所以log2 可以提出来。

当 P(x) 和 Q(x) 不重叠的时候，JS(P||Q) 的后2项为0。 我们可以参考下图理解：
当P和Q 不重叠的时候 即在x=5处，此时p(x) = q(x) = 0,
当x>=5时，P 近似0：
$$\frac{1}{2}\sum p(x)log\frac{p(x)}{p(x)+q(x)}+\frac{1}{2}\sum q(x)log\frac{q(x)}{p(x)+q(x)}=\frac{1}{2}\sum 0log\frac{0}{0+q(x)}+\frac{1}{2}\sum q(x)log\frac{q(x)}{0+q(x)}=0$$
当x<5时，Q近似0：
$$\frac{1}{2}\sum p(x)log\frac{p(x)}{p(x)+q(x)}+\frac{1}{2}\sum q(x)log\frac{q(x)}{p(x)+q(x)}=\frac{1}{2}\sum p(x)log\frac{p(x)}{p(x)+0}+\frac{1}{2}\sum 0log\frac{0}{p(x)+0}=0$$

所以得出，当P Q 不重叠的时候， JSD(P||Q) = log2.
这也是JSD的缺陷，当两个分部完全不重叠的时候， 即便2个分布的中心距离有多近或者多远，JS散度一直是一个常数，以至于梯度为0, 无法更新。

Wasserstein 距离

又称 EM距离（EarthMover距离），推土距离。输出没有上下界。
用来衡量2个分部之间的距离，定义如下：
$$W(P_1,P_2)=in{f}_{\gamma \prod (P_1,P_2)}{E}_{(x,y)\gamma }[||x-y||]$$
其中$\prod (P_1,P_2)$ 是P1和P2分布组合起来的所有可能的联合分布的集合。 对于每一个可能的联合分布$\gamma$,可以从中采样(x,y) 得到一个样本x 和 y，并计算出这对样本的距离||x-y||，所以可以计算该联合分布$\gamma$下，样本对距离的期望值$E_{(x,y)\gamma }[||x-y||]$. 在所有可能的联合分布中，能够对这个期望值取到的下界 就是 wasserstein距离。

假设有两堆数据分布 P和 Q，看作两堆土，现在把 P 这堆土推成 Q 这堆土所需要的最少的距离就是 EM 距离：

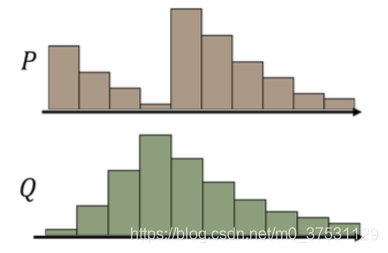
假设 P 的分布是上图棕色柱块区域，Q 的分布是上图绿色柱块区域，现在需要把 P 的 分布推成 Q 的分布，我们可以制定出很多不同的 MovingPlan(推土计划)。

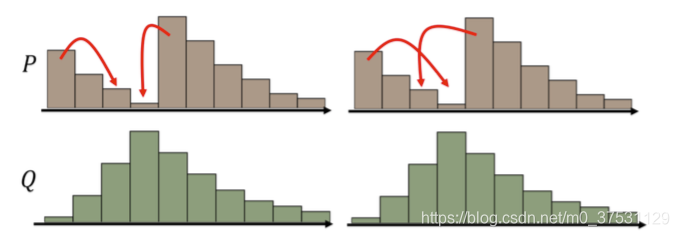
这些不同的推土计划都能把分布 P 变成分布 Q，但是它们所要走的平均推土距离是不 一样的，我们最终选取最小的平均推土距离值作为 EM 距离。例如上面这个例子的 EM 距离 就是下面这个推土方案对应的值。

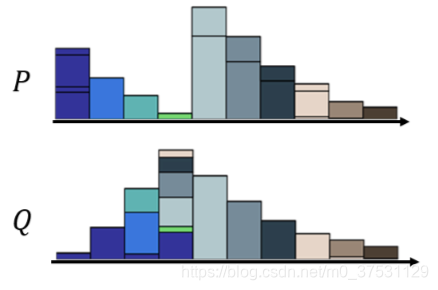
那为了更好地表示这个推土问题，我们可以把每一个 moving plan 转化为一个矩阵图:

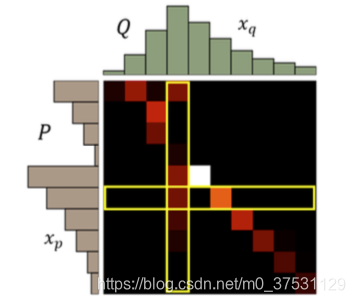
每一个色块表示 P 分布到 Q 分布需要分配的土量(移动距离)，那每一行的色块之和就 是 P 分布该行位置的柱高度，每一列的色块之和就是 Q 分布该列位置的柱高度。
此时的表达式就为：

EM距离相比KL散度和JS散度的优势在于， 即使两个分布的支撑集中没有重叠或者重叠非常少，仍然能反映两个分布的远近，而JS 散度此时是一个常数，KL散度此时无意义。

JS 散度
EM距离