离散数学基础-集合

离散数学基础-集合

1、集合

定义: 由不同对象聚集而成的一个整体, 集合中的对象成为成员或元素.

x属于集合S， 记为x∈S，x不是集合S中的成员记为x∉S。

比如S={1, 2, 3}, 2∈S, 集合中的元素是唯一的,如{1,2,3,4,1} = {1,2,3,4} = {4,3,2,1}, 集合是无序的. 说明: 有的把包含多个相同元素的集合称为多重集.是集合的一种变体.

2、常见集合表示

Ø表示空集合, 即集合中不包含任何元素.

Z表示整数集合, 即集合{1,2,3,-1,-2,-3,0}.

R表示实数集合

N表示自然数集合{0,1,2,3…}.

若B包含A中的所有元素, 称A是B的子集.记为A⊆B.

若A⊆B且A!=B, 称集合A是B的真子集.

3、集合的基本操作

A∩B = {x:x∈A且x∈B}, 记为A与B集合的交集.

A∪B = {x:x∈A或x∈B}, 记为A与B的并集.

A-B = {x:x∈A且x∉B},记为A的差集.(就是前面减后面, 保留在A中的，且不在B中的), 如{1,2,3} - {2,3} = {1}

A∩Ø = Ø, 表示任意集合与空集合的交集为空集合.

A∪Ø = A, A∩A= A, A∪A= A

交换律: A∩B=B∩A, A∪B=B∪A

结合律A∩(B∩C)=(A∩B)∩C, A∪(B∪C)=(A∪B)∪C

分配律:A∩(B∪C)=(A∩B)∪(A∩C), A∪(B∩C)=(A∪B)∩(A∪C)

吸收律:A∩(A∪B)=A, A∪(A∩B)=A.

用做图说明吸收律

第二个同理. 说明:图式只能用于说明，但不能用于严格的证明.

4、德.摩根定律:

A-(B∩C)=(A-B)∪(A-C)
A-(B∪C)=(A-B)∩(A-C)

以上也可用图式说明.这里就不画图了.

5、全集与补集

我们称U为集合的全集, 集合A的补集为: 图片 = U-A={x: x∈U且x∉A}

有如下法则:

集合A的补的补还是A

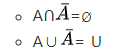
德.摩根定律集合补的形式(手敲不太好敲, 截个图):

6、笛卡尔积

表示为AXB，是第一个元素为A中的成员, 第二个元素为B中的成员的所有有序对的集合,记为AXB={(a,b):a∈A且b∈B}

例如:{a,b}X{a,b,c} = {(a,a),(a,b),(a,c),(b,a),(b,b),(b,c)}.

今天就到这里，集合知识相对好理解，有兴趣的可以看看集合论.