Numerical Optimization Ch19.Interior-Point Methods for Nonlinear Programming

第十九章: 非线性规划的内点法

现已证实, 内点法不仅在线性规划上, 在非线性规划问题上也同样有出色的表现. 与积极集SQP算法一起, 它们是当前公认的求解大规模非线性规划最有力的算法. 一些关键的概念, 诸如原始-对偶迭代步, 可以直接从线性规划的情形拿过来. 但与此同时也产生了一些新的挑战, 包括 如何处理非凸性质、如何在非线性性存在时更新障碍因子(即之前的惩罚因子)以及如何保证算法收敛到解. 本章我们介绍两种已在实际应用中有较好表现的内点法.

• 第一类算法可视为是线性和二次规划内点法的直接拓展. 它们使用线搜索强制收敛, 利用数值线性代数的方法(如矩阵分解)计算迭代步.
• 第二类的方法则使用二次模型定义迭代步, 并包含了信赖域的约束以增强稳定性.

这两种算法分别与线搜索和信赖域SQP算法具有相似的渐进性质.

非线性优化的障碍函数法(barrier methods)于上世纪六十年代被提出, 但在之后的近20年内淡出. 而内点法在线性规划上的成功应用则再次点燃了研究者们对它们在非线性情形研究的热情. 到上世纪九十年代末期, 已有对于非线性规划的新一代的算法和软件产生. 数值实验表明内点法在大型问题上往往要快于积极集SQP算法, 尤其是在自由变量的数目比较大的时候. 它们可能还不是很鲁棒, 但关于它们的设计和实施上的改进一直在进行. 现在, "内点法"和"障碍函数法"这两个词往往不加分别地互用.

在第十四章和第十六章, 我们分别讨论了线性规划和二次规划的内点法. 读者并不需要提前看过这两章. 本章的第一部分是关于KKT条件和牛顿法, 而第二部分则与第十八章SQP对应.

本章考虑的问题可写成如下形式:$$\begin{array}{rl}\underset{x,s}{\min }& f(x)\\ \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& c_E(x)=0,\\ & c_I(x)-s=0,\\ & s\ge 0.\end{array}$$其中向量$c_I(x)$从标量函数$c_i(x),i\in \mathcal{I}$构建; $c_E(x)$类似. 注意我们引入了松弛变量$s$将不等式约束$c_I(x)\ge 0$转换成了等式约束. 我们用$l$表示等式约束数量, $m$表示不等式约束数量.

1. 两种解释

内点法有两种解释的方式. 一种是连续方法(可见第十四章), 一种是障碍函数法.

1.1 连续/同伦方法的观点

非线性规划的KKT条件为$$\begin{array}{rl}\nabla f(x)-A_E^T(x)y-A_I^T(x)z& =0,\\ Sz-\mu e& =0,\\ c_E(x)& =0,\\ c_I(x)-s& =0,\end{array}$$其中$\mu =0,s\ge 0,z\ge 0$. 这里$A_E(x),A_I(x)$分别是$c_E,c_I$的Jacobi阵, $y,z$为对应的Lagrange乘子. 我们定义$S,Z$分别为向量$s,z$生成的对角阵.

这里, 互补松弛条件($\mu =0$)以及界约束$s\ge 0,z\ge 0$会引入组合方面的困难. 可见第十五章例1. 我们可令$\mu$严格大于0, 绕过这个问题, 从而强制$s,z$取正值. 同伦(或连续)方法就是对一列正参数 { μ k } : μ k → 0 \{\mu_k\}:\mu_k\to0 {μk​}:μk​→0(近似)求解一系列的扰动KKT方程, 同时保持$s,z>0$. 我们希望, 在极限状态下, 我们能得到一满足KKT条件的解. 进一步地, 通过要求迭代点减小价值函数(或被滤子所接受), 则最终收敛到的就是极小点而不仅仅是KKT点.

同伦方法是局部意义的算法. 假设解$(x^{\ast },s^{\ast },y^{\ast },z^{\ast })$满足LICQ、严格互补松弛条件和二阶充分性条件, 则在其一邻域内, 对所有充分大的$\mu$, 系统将会有局部的唯一解, 我们以$(x(\mu ),s(\mu ),y(\mu ),z(\mu ))$表示. 由这些点构成的轨迹被称为原始-对偶中心路径, 它随$\mu \to 0$收敛于$(x^{\ast },s^{\ast },y^{\ast },z^{\ast })$.

1.2 障碍函数的观点

第二种内点法的解释考虑障碍问题(barrier problem)$$\begin{array}{rl}\underset{x,s}{\min }& f(x)-\mu \sum _{i=1}^m\log s_i\\ \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& c_E(x)=0,\\ & c_I(x)-s=0,\end{array}$$其中$\mu$为正参数. 因为障碍项$-\mu {\sum }_{i=1}^m\log s_i$的存在, 我们不需要考虑$s\ge 0$. 事实上, 障碍项能够避免$s$的分量离0太近. 障碍问题同样也避免了非线性规划的组合困难, 但它在$\mu >0$的解并不与非线性规划的解契合, 这点与同伦方法相同. 障碍函数法就是对一列正障碍因子 { μ k } : μ k → 0 \{\mu_k\}:\mu_k\to0 {μk​}:μk​→0, (近似)求解一系列障碍问题.

1.3 两种观点的比较

为比较两种观点, 我们将障碍问题的KKT条件写出:$$\begin{array}{rl}\nabla f(x)-A_E^T(x)y-A_I^T(x)z& =0,\\ -\mu S^{-1}e+z& =0,\\ c_E(x)& =0,\\ c_I(x)-s& =0.\end{array}$$注意这与扰动KKT方程只有第二个等式不同. 这里在$s\to 0$时会趋向非线性. 为使用牛顿法, 我们有必要将第二行的有理式转变成二次方程. 于是左乘$S$(这不会改变KKT系统的解, 因为$S$的对角元都是正数), 就与扰动KKT方程相同了.

"内点"这个词是因为早期的障碍函数法并不使用松弛变量, 且假设初始点对不等式约束$c_i(x)\ge 0,i\in \mathcal{I}$是可行的. 这些算法使用障碍函数$$f(x)-\mu \sum _{i\in \mathcal{I}}\log c_i(x)$$防止迭代点从由不等式约束定义的可行域中脱离. 我们将在第6节讨论这个障碍函数. 而大多数现代的内点法都是不可行方法(它们可从任意点$x_0$出发), 并只保证迭代点位于$s\ge 0,z\ge 0$张成区域的内部. 不过, 它们可以在一个可行点产生后, 保证后续所有的迭代点都是可行的.

之后我们将说明同伦和障碍函数的观点都是有用的. 具体来说, 同伦的观点给出了原始-对偶方向的定义, 而障碍函数的观点则有助于设计全局收敛的迭代.

2. 一个基本的内点法算法

将牛顿法应用于扰动KKT方程, 我们有$$\left[\begin{array}{cccc}{\nabla }_{xx}^2\mathcal{L}& O& -A_E^T(x)& -A_I^T(x)\\ O& Z& O& S\\ A_E(x)& O& O& O\\ A_I(x)& -I& O& O\end{array}\right]\left[\begin{array}{c}{p}_x\\ p_s\\ p_y\\ p_z\end{array}\right]=-\left[\begin{array}{c}\nabla f(x)-A_E^T(x)y-A_I^T(x)z\\ Sz-\mu e\\ c_E(x)\\ c_I(x)-s\end{array}\right],$$其中$\mathcal{L}$表示Lagrange函数$$\mathcal{L}(x,s,y,z)=f(x)-y^T{c}_E(x)-z^T(c_I(x)-s).$$上述方程称为原始-对偶系统(primal-dual system). 在计算出$p=(p_x,p_s,p_y,p_z)$后, 我们就令新迭代点$(x^{+},s^{+},y^{+},z^{+})$为$$\begin{array}{rl}{x}^{+}& =x+{\alpha }_s^{\max }{p}_x,s^{+}=s+{\alpha }_s^{\max }{p}_s,\\ y^{+}& =y+{\alpha }_z^{\max }{p}_y,z^{+}=z+{\alpha }_z^{\max }{p}_z,\end{array}$$其中 α s max ⁡ = max ⁡ { α ∈ ( 0 , 1 ] : s + α p s ≥ ( 1 − τ ) s } , α z max ⁡ = max ⁡ { α ∈ ( 0 , 1 ] : z + α p z ≥ ( 1 − τ ) z } , \begin{aligned}\alpha_s^{\max}&=\max\{\alpha\in(0,1]:s+\alpha p_s\ge(1-\tau)s\},\\\alpha_z^{\max}&=\max\{\alpha\in(0,1]:z+\alpha p_z\ge(1-\tau)z\},\end{aligned} αsmax​αzmax​​=max{α∈(0,1]:s+αps​≥(1−τ)s},=max{α∈(0,1]:z+αpz​≥(1−τ)z},​$\tau \in (0,1)$. 比如可取$\tau =0.995$. 上述确定步长$\alpha$的条件称为是分数到边准则(fraction to the boundary rule), 这使得$s,Z$不会过快地趋近于它们的下界$0$.

尽管还有许多细节需要考虑, 比如需要处理非凸性和非线性性, 但这种简单的迭代方式提供了现代内点法的基础. 算法其他的主要部分还包括选取障碍因子序列 { μ k } \{\mu_k\} {μk​}. Fiacco和McCormick¹的方法是固定$\mu$直到KKT条件在一定精度下满足. 另一种就是在每次迭代都对其进行更新. 两者均有各自的优点, 我们将在第3节讨论之.

由于迭代最终收敛到满足二阶充分性条件和严格互补松弛条件的解, 因此原始-对偶矩阵(或KKT矩阵)保持非奇异. 更确切地说, 若$x^{\ast }$为严格互补松弛条件成立的解, 则随着迭代点趋近于$x^{\ast }$, 对每个指标$i$, $s_i$或$z_i$有且仅有一个远离0, 这就保证了KKT矩阵的第二行行满秩. 因此, 内点法本身不会有病态或者奇异的问题. 而这一事实也使我们能对其建立快速(超线性)的局部收敛速度定理. 可见第8节.

我们使用以下基于扰动KKT方程的误差函数作为某种形式上的价值函数: E ( x , s , y , z ; μ ) = max ⁡ { ∥ ∇ f ( x ) − A E ( x ) T y − A I ( x ) T z ∥ , ∥ S z − μ e ∥ , ∥ c E ( x ) ∥ , ∥ c I ( x ) − s ∥ } , \begin{aligned}E(x,s,y,z;\mu)=\max\{\Vert\nabla &f(x)-A_E(x)^Ty-A_I(x)^Tz\Vert,\Vert Sz-\mu e\Vert,\\&\Vert c_E(x)\Vert,\Vert c_I(x)-s\Vert\},\end{aligned} E(x,s,y,z;μ)=max{∥∇​f(x)−AE​(x)Ty−AI​(x)Tz∥,∥Sz−μe∥,∥cE​(x)∥,∥cI​(x)−s∥},​其中$\Vert \cdot \Vert$为某一向量范数.

算法1 (Basic Interior-Point Algorithm)
Choose $x_0$ and $s_0>0$, and compute initial values for the multipliers $y_0$ and $z_0>0$.
Select an initial barrier parameter ${\mu }_0>0$ and parameters $\sigma ,\tau \in (0,1)$.
Set $k\leftarrow 0$
repeat until a stopping test for the nonlinear program is satisfied
\quad\quad repeat until $E(x_k,s_k,y_k,z_k;{\mu }_k)\le {\mu }_k$
\quad\quad\quad\quad Solve the perturbed KKT system to obtain the search direction $p=(p_x,p_s,p_y,p_z)$;
\quad\quad\quad\quad Compute ${\alpha }_s^{\max },{\alpha }_z^{\max }$;
\quad\quad\quad\quad Compute $(x_{k+1},s_{k+1},y_{k+1},z_{k+1})$;
\quad\quad\quad\quad Set ${\mu }_{k+1}\leftarrow {\mu }_k$ and $k\leftarrow k+1$;
\quad\quad end
\quad\quad Choose ${\mu }_k\in (0,\sigma {\mu }_k)$;
end

每步迭代均更新${\mu }_k$的算法则只需要把算法1中的内循环拿掉, 再把倒数第二行${\mu }_k$的更新方式做一些修正即可.

下面的定理提供了仅计算障碍问题近似解的内点法的理论支撑.

定理1 假设算法1产生了一列迭代点 { x k } \{x_k\} {xk​}且 { μ k } → 0 \{\mu_k\}\to0 {μk​}→0(即算法的内循环不会无穷地进行下去). 设$f,c$为连续可微函数. 则 { x k } \{x_k\} {xk​}的所有聚点$\hat{x}$都是可行点. 进一步, 任何满足LICQ的 { x k } \{x_k\} {xk​}的聚点$\hat{x}$都是KKT点.

证明: 简单起见, 我们仅证明包含不等式约束的情形, 且以$c$表示原本的不等式约束$c_I$. 令$\hat{x}$为 { x k } \{x_k\} {xk​}的极限点, 且 { x k l } \{x_{k_l}\} {xkl​​}为相应的收敛子列: { x k l } → x ^ \{x_{k_l}\}\to\hat x {xkl​​}→x^. 因为${\mu }_k\to 0$, 所以$E$收敛到0, 于是$(c_{k_l}-s_{k_l})\to 0$. 由$c$的连续性, 这就表明$\hat{c}\stackrel{def}{=}c(\hat{x})\ge 0$(即$\hat{x}$可行)以及$s_{k_l}\to \hat{s}=\hat{c}$.

现假设在$\hat{x}$处满足LICQ, 考虑积极集 A = { i : c ^ i = 0 } . \mathcal{A}=\{i:\hat c_i=0\}. A={i:c^i​=0}.对$i\notin \mathcal{A}$, 我们有${\hat{c}}_i>0,{\hat{s}}_i>0$, 因此由严格互补松弛条件, { z k l } i → 0 \{z_{k_l}\}_i\to0 {zkl​​}i​→0. 由$E$的定义, 我们有$\nabla f_{k_l}-A_{k_l}^T{z}_{k_l}\to 0$, 结合上一段, 有$$\nabla f_{k_l}-\sum _{i\in \mathcal{A}}[z_{k_l}{]}_i\nabla c_i(x_{k_l})\to 0.$$由LICQ, 向量 { ∇ c ^ i : i ∈ A } \{\nabla\hat c_i:i\in\mathcal{A}\} {∇c^i​:i∈A}线性无关. 于是由$\nabla f(\cdot ),\nabla c_{(i)}(\cdot ),i\in \mathcal{A}$的连续性, 正序列 { z k l } \{z_{k_l}\} {zkl​​}收敛于某个$\hat{z}\ge 0$. 在上式两端取极限就有$$\nabla f(\hat{x})=\sum _{i\in \mathcal{A}}{\hat{z}}_i\nabla c_i(\hat{x}).$$由积极集和严格互补松弛条件, 还有${\hat{c}}^T\hat{z}=0$. 证毕.

实用内点法分为两类. 第一类以算法1为基础, 并加入线搜索和控制$s,z$下降速率的技术, 且引入对非负曲率的讨论. 第二类可见第5节, 极小化障碍问题的二次模型, 同时受限于信赖域约束. 这两类方法有许多的共同点.

3. 算法1的进一步讨论

现在我们讨论算法1的一些修正和拓展, 以让它能在非线性非凸问题上继续发挥作用.

通常, 原始-对偶系统写作$$\left[\begin{array}{cccc}{\nabla }_{xx}^2\mathcal{L}& O& A_E^T(x)& A_I^T(x)\\ O& \Sigma & O& -I\\ A_E(x)& O& O& O\\ A_I(x)& -I& O& O\end{array}\right]\left[\begin{array}{c}{p}_x\\ p_s\\ -p_y\\ -p_z\end{array}\right]=-\left[\begin{array}{c}\nabla f(x)-A_E^T(x)y-A_I^T(x)z\\ z-\mu S^{-1}e\\ c_E(x)\\ c_I(x)-s\end{array}\right],$$其中$$\Sigma =S^{-1}Z.$$这样我们就可使用对称线性方程的求解器. 每步迭代的计算量就会有所减少.

3.1 原始系统 vs. 原始-对偶系统

如果我们直接对障碍问题的最优性条件应用牛顿法, 之后再对称化迭代矩阵, 我们就会得到类似的系数矩阵, 但此时$$\Sigma =\mu S^{-2}.$$此系统通常称为原始系统(primal system). 这样的命名主要是基于内点法发展的历史.

即使原问题和障碍问题等价, 直接使用牛顿法也通常会产生不同的迭代点. 而原始-对偶系统往往更受青睐. 注意原问题KKT条件的互补松弛条件导数是有界的, 但障碍问题却不具有这样的性质. 进一步地, 关于原始步的分析和一些实验结果都表明, 在某些情形下原始系统将产生破坏$s>0,z>0$约束的迭代步. 从而减缓进程. 可见第6节.

3.2 求解原始-对偶系统

除了计算函数值和导数值的计算量, 内点法的计算花费主要是在求解原始-对偶系统上. 因此高效的(使用稀疏分解或迭代技术的)线性求解器在大型问题的快速求解上至关重要.

• 构造.
  由于原始-对偶系统的系数对称矩阵与第十六章中的KKT矩阵很相似, 因此这样的系统可以用第十六章中方法求解. 我们首先用第二行消去$p_s$, 得到$$\left[\begin{array}{ccc}{\nabla }_{xx}^2\mathcal{L}& A_E^T(x)& A_I^T(x)\\ A_E(x)& O& O\\ A_I(x)& O& -{\Sigma }^{-1}\end{array}\right]\left[\begin{array}{c}{p}_x\\ -p_y\\ -p_z\end{array}\right]=-\left[\begin{array}{c}\nabla f(x)-A_E^T(x)y-A_I^T(x)z\\ c_E(x)\\ c_I(x)-\mu Z^{-1}e\end{array}\right].$$此系统可用对称不定分解求解: 记此系数矩阵为$K$, 则对称不定分解计算$P^{T}KP=LB{L}^T$, 其中$L$为下三角阵, $B$分块对角, 其中对角块为$1\times 1$或$2\times 2$的子阵. $P$为排列矩阵, 用于权衡稀疏性和数值稳定性.
  此系统可进一步用最后一行消去$p_z$, 得到更加约减的系数矩阵$$\left[\begin{array}{cc}{\nabla }_{xx}^2\mathcal{L}+A_I^T\Sigma A_I& A_E^T(x)\\ A_E(x)& O\end{array}\right],$$这步约减在不等式约束很多的时候尤其显著. 尽管$A_I^T\Sigma A_I$会带来显著的填充, 但这在许多应用中都还是可接受的. 当然最理想的情形是$A_I^T\Sigma A_I$对角. 不等式约束都是界约束时就是这种情形.
• 病态与求解方法.
  • 不论是什么形式, 原始-对偶系统都是病态的, 这是因为$\Sigma$的某些元素将随着$\mu \to 0$发散到$\infty$, 而其他的则会收敛到$0$. 尽管如此, 由于此病态结构具有特殊形式, 由稳定的直接分解法计算的方向通常还是精确的. 只有当松弛变量$s$或乘子$z$非常靠近$0$(或当Hessian阵${\nabla }_{xx}^2\mathcal{L}$或$A_E$几近亏秩)时才会导致毁灭性的误差. 基于此, 直接分解法被认为是在内点法计算迭代步时最可靠的技术.
  • 我们自然也可以使用迭代的技术. 如此一来病态就是个严重的问题, 因此必须使用合适的预处理子. 幸运的是, 这样的预处理子很容易构造. 例如我们在原始-对偶系统里引入${\tilde{p}}_s=S^{-1}{p}_s$, 在第二个方程上左乘$S$, 将$\Sigma$转变为$S\Sigma S$. 随着$\mu \to 0$(且假设$SZ\approx \mu I$), $S\Sigma S$就接近于$\mu I$. 当然还有其他的变尺度方法. 例如引入变量${\tilde{p}}_s={\Sigma }^{1/2}{p}_s$就得到了完美的预处理子, 而若${\tilde{p}}_s=\sqrt{\mu }{S}^{-1}{p}_s$就将$\Sigma$转换成$S\Sigma S/\mu$, 这在$\mu \to 0$时收敛到$I$.
    我们可以用迭代的方法求解以上任何一个对称不定系统. 这里CG就不太合适了, 毕竟它只适用于正定系统. 我们可以用GMRES, QMR或LSQR. 除了使用预处理缓解由障碍函数带来的病态, 我们还需要处理由Hessian${\nabla }_{xx}^2\mathcal{L}$或Jacobi阵$A_E,A_I$带来的问题. 对此我们很难找到一般性的预处理子.
    一种高效的替代方案是使用零空间方法求解原始-对偶系统并将CG用于(正定)既约空间, 如第十六章. 我们可用带约束预处理子的投影CG. 就原始-对偶系统而言, 预处理子有形式$$\left[\begin{array}{cccc}G& O& A_E^T(x)& A_I^T(x)\\ O& T& O& -I\\ A_E(x)& O& O& O\\ A_I(x)& -I& O& O\end{array}\right],$$其中$G$为稀疏阵, 他在约束的零空间上正定; $T$为对角阵, 等于或近似$\Sigma$. 此预处理子保留了$A_E,A_I$, 从而去除了由这些矩阵带来的病态问题.

3.3 更新障碍因子

障碍因子序列 { μ k } \{\mu_k\} {μk​}必须收敛于$0$, 从而使我们在极限状态下能得到原问题的解. 若${\mu }_k$下降过慢, 则就需要过多的迭代; 若下降太快, 则$s$或$z$的某些分量可能会过早地趋向于$0$, 减缓迭代进程. 下面介绍几种更新${\mu }_k$的高效实用技术.

3.3.1 Fiacco-McCormick策略

在算法1中的Fiacco-McCormick策略是固定障碍因子直到扰动的KKT条件达到一定的精度. 之后障碍因子以如下形式更新:$${\mu }_{k+1}={\sigma }_k{\mu }_k,{\sigma }_k\in (0,1).$$一些早期的内点法选取${\sigma }_k$为一个常数(比如$0.2$). 然而让${\sigma }_k$多取几个值应当更好些(比如$0.2,0.1$): 当最近几步迭代效果显著时, 就选取较小的值. 进一步, 在解附近令${\sigma }_k\to 0$再让$\tau \to 1$, 我们就有超线性局部收敛速度.

Fiacco-McCormick策略在许多问题上都适用, 但它对初始点、初始障碍因子的选取以及问题的尺度很敏感.

3.3.2 自适应更新策略

自适应的更新策略则在复杂困难的情形更加鲁棒. 这些策略不像Fiacco-McCormick策略, 将根据算法的进程, 在每一步都更新$\mu$. 大多这样的策略都基于互补松弛条件, 这如同线性规划的情形(可见第十四章). 它们具有形式$${\mu }_{k+1}={\sigma }_k\frac{s_k^T{z}_k}{m},$$这就使得${\mu }_k$能反映问题的尺度. 而我们对于${\sigma }_k$的选取, 则基于最小的互补乘积:$${\sigma }_k=0.1\min {\left(0.05\frac{1-{\xi }_k}{{\xi }_k},2\right)}^3,{\xi }_k=\frac{{\min }_i[s_k{]}_i[z_k{]}_i}{(s^k{)}^T{z}^k/m}.$$这里$[\cdot {]}_i$表示取出第$i$个分量. 当${\xi }_k\approx 1$(即所有的对偶乘积就接近它们的平均值), 障碍因子就会剧烈减小.
预估或是测探策略(可见第十四章)亦可以用来给出${\sigma }_k$. 我们首先令$\mu =0$计算得到预估(仿射尺度变换)步$$(\Delta x^{\mathrm{a}\mathrm{f}\mathrm{f}},\Delta s^{\mathrm{a}\mathrm{f}\mathrm{f}},\Delta y^{\mathrm{a}\mathrm{f}\mathrm{f}},\Delta z^{\mathrm{a}\mathrm{f}\mathrm{f}}).$$之后我们沿此方向探查得到${\alpha }_p^{\mathrm{a}\mathrm{f}\mathrm{f}},{\alpha }_d^{\mathrm{a}\mathrm{f}\mathrm{f}}$为(不打破$(s,z)\ge 0$)最大步长. 这些迭代步长都具有显式的表达式(即令$\tau =1$). 之后定义${\mu }_{\mathrm{a}\mathrm{f}\mathrm{f}}$为$${\mu }_{\mathrm{a}\mathrm{f}\mathrm{f}}=\frac{(s_k+{\alpha }_s^{\mathrm{a}\mathrm{f}\mathrm{f}}\Delta s^{\mathrm{a}\mathrm{f}\mathrm{f}}{)}^T(z_k+{\alpha }_z^{\mathrm{a}\mathrm{f}\mathrm{f}}\Delta z^{\mathrm{a}\mathrm{f}\mathrm{f}})}{m},$$并定义${\sigma }_k$为如下:$${\sigma }_k={\left(\frac{{\mu }_{\mathrm{a}\mathrm{f}\mathrm{f}}}{s_k^T{z}_k/m}\right)}^3.$$这种${\sigma }_k$的启发式选取在线性规划问题的内点法中提出, 且同样适用于非线性规划.

3.4 处理非凸与奇异性

由原始-对偶系统定义的方向并不总有较好的效果, 因为它只定位KKT点; 这就意味着它可以趋向极大点或者是其他稳定点. 在第十八章, 我们知道若Hessian阵$W$在约束的切空间正定, 则对等式约束问题牛顿步对一大类价值函数保证是个下降方向, 同时对于滤子也是个有用的方向. 理由是, 此时的牛顿步可看做是在通过消去线性化约束得到的既约空间上极小化一个凸模型.

而对于原始-对偶系统则类似, $p$为下降方向若$$\left[\begin{array}{cc}{\nabla }_{xx}^2\mathcal{L}& O\\ O& \Sigma \end{array}\right]$$在$$\left[\begin{array}{cc}{A}_E(x)& O\\ A_I(x)& -I\end{array}\right]$$的零空间上正定. 第十六章的关于惯性指数的定理3则指出, 若原始-对偶矩阵的惯性指数为$$(n+m,l+m,0),$$则此正定性条件成立. 换句话说, 原始-对偶矩阵要恰好有$n+m$个正特征值, $l+m$个负特征值以及没有0特征值. 而若原始-对偶矩阵没有这样的惯性指数, 我们也可以对它修正. 注意对角阵$\Sigma$正定, 而${\nabla }_{xx}^2\mathcal{L}$可以是不定的. 因此我们以${\nabla }_{xx}^2\mathcal{L}+\delta I$代替后者, 其中$\delta >0$充分大以保证惯性指数条件成立. 这种修正的量事先是未知的, 但我们可以连续增大$\delta$直到条件满足.

我们也必须考虑由$A_E$亏秩带来的奇异性. 我们可以额外再增加一个正则化参数$\gamma \ge 0$. 最后修正的原始-对偶矩阵为$$\left[\begin{array}{cccc}{\nabla }_{xx}^2\mathcal{L}+\delta I& O& A_E(x{)}^T& A_I(x{)}^T\\ O& \Sigma & O& -I\\ A_E(x)& O& -\gamma I& O\\ A_I(x)& -I& O& O\end{array}\right].$$一种选取$\delta ,\gamma$的程序如下:

程序2 (Inertia Correction and Regularization)
Given the current barrier parameter $\mu$, constants $\eta >0$ and $\beta <1$, and the perturbation ${\delta }_{old}$ used in the previous interior-point iteration
Factor the modified primal-dual matrix with $\delta =\gamma =0$.
if the modified primal-dual matrix is nonsingular and its inertia is $(n+m,l+m,0)$
\quad\quad Compute the primal-dual step; stop;
if the modified primal-dual matrix has zero eigenvalues
\quad\quad set $\gamma \leftarrow 10^{-8}\eta {\mu }^{\beta }$;
if ${\delta }_{old}=0$
\quad\quad set $\delta \leftarrow 10^{-4}$;
else
\quad\quad set $\delta \leftarrow {\delta }_{old}/2$;
repeat
\quad\quad Factor the modified matrix;
\quad\quad if the inertia is $(n+m,l+m,0)$
\quad\quad\quad\quad Set ${\delta }_{old}\leftarrow \delta$;
\quad\quad\quad\quad Compute the primal-dual step using the modified matrix; stop;
\quad\quad else
\quad\quad\quad\quad Set $\delta \leftarrow 10\delta$;
end (repeat)

程序2需要在内点法的每一次迭代调用, 以强制满足惯性指数条件, 保证非奇异性. 其他的保证修正的矩阵正定性的策略可见第三章.

3.5 步长接收机制: 价值函数与滤子

价值函数或滤子的作用是决定一试探步是否应当被接收. 由于内点法可以看做是求解障碍问题的方法, 因此以障碍函数的形式定义价值函数$\varphi$或滤子是合适的. 例如我们可以使用精确价值函数$${\varphi }_v(x,s)=f(x)-\mu \sum _{i=1}^m\log s_i+v\Vert c_E(x)\Vert +v\Vert c_I(x)-s\Vert ,$$其中范数可选比如$l_1$或$l_2$范数. 惩罚因子$v>0$可用第十八章中的策略更新.
在线搜索算法中, 在计算出$p$和最大的步长后, 我们使用回溯线搜索计算步长$${\alpha }_s\in (0,{\alpha }_s^{\max }],{\alpha }_z\in (0,{\alpha }_z^{\max }],$$以得到价值函数的充分下降或确保为滤子所接收. 于是新的迭代点定义为$$\begin{array}{rl}{x}^{+}& =x+{\alpha }_s{p}_x,s^{+}=s+{\alpha }_s{p}_s,\\ y^{+}& =y+{\alpha }_z{p}_y,z^{+}=z+{\alpha }_z{p}_z.\end{array}$$定义滤子需要同时考虑障碍函数$f(x)-\mu {\sum }_{i=1}^m\log s_i$和约束违反度$\Vert (c_E(x),c_I(x)-s)\Vert$. 若$p$不被任何滤子中的元素占优, 则就可被接收. 在特定情形下(比如当前步长过小), 若$p$不被滤子所接收, 我们不会继续减少步长${\alpha }_s$, 而是调用可行性恢复阶段.

3.6 拟牛顿近似

原始-对偶矩阵的拟牛顿版本是要用拟牛顿近似$B$替换${\nabla }_{xx}^2\mathcal{L}$. 我们可以用BFGS或SR1更新公式, 或是使用有限内存BFGS公式定义$B$. 我们近似非线性规划Lagrange函数的Hessian而不是障碍函数的Hessian, 是因为后者高度病态且变化迅速.

我们这里用$(\delta x,\delta l)$表示拟牛顿更新公式使用的校正对. 在计算从$(x,s,y,z)$到$(x^{+},s^{+},y^{+},z^{+})$的迭代步后, 我们定义$$\begin{array}{rl}\Delta l& ={\nabla }_x\mathcal{L}(x^{+},s^{+},y^{+},z^{+})-{\nabla }_x\mathcal{L}(x,s^{+},y^{+},z^{+}),\\ \Delta x& =x^{+}-x.\end{array}$$为确保BFGS算法产生正定阵, 我们可以选择跳步或阻滞策略. 而SR1更新则必须避免无界情形的发生, 且可能需要修正以使得惯性指数条件成立. 此修正可用程序2实现.

以上得到的拟牛顿矩阵$B$是稠密的$n\times n$矩阵. 对于大型的问题, 有限内存的更新更受青睐. 一种实施有限内存BFGS算法的方式是利用第七章介绍的紧表示. 于是$B$有形式$$B=\xi I+WM{W}^T,$$其中$\xi >0$为尺度因子, $W$为$n\times 2\hat{m}$矩阵, $M$为$2\hat{m}\times 2\hat{m}$对称可逆阵, $\hat{m}$为有限内存中储存的校正对的个数. $W,M$使用前$\hat{m}$次迭代累积的 { Δ l k } , { Δ x k } \{\Delta l^k\},\{\Delta x^k\} {Δlk},{Δxk}产生. 因有限内存矩阵$B$正定且假定$A_E$满秩, 于是原始-对偶矩阵非奇异, 我们可用Sherman-Morrison-Woodbury公式求解修正原始-对偶方程. 事实上, 修正的原始-对偶矩阵可写为$$\left[\begin{array}{cccc}\xi I& O& A_E^T& A_I^T\\ O& \Sigma & O& I\\ A_E& O& O& O\\ A_I& I& O& O\end{array}\right]+\left[\begin{array}{c}W\\ O\\ O\\ O\end{array}\right]\left[\begin{array}{cccc}M{W}^T& O& O& O\end{array}\right].$$

3.7 可行内点法

许多应用中, 我们希望算法产生的所有迭代点对某些或所有的不等式约束都是可行的. 例如当目标函数只有在某些约束满足时才有定义.

内点法提供了推导可行算法的一个天然的框架. 若当前迭代点$x$满足$c_I(x)>0$, 则我们很容易就能对由原始-对偶方程得到的迭代步修改, 使得下一迭代点满足可行性. 具体说来, 在计算$p$后, 令$x^{+}=x+p_x$, 重新定义松弛变量为$$s^{+}\leftarrow c_I(x^{+}),$$并检验$(x^{+},s^{+})$是否为价值函数$\varphi$接受. 若是, 则定义此试探点为新点; 否则拒绝$p$, 并以更短的步长计算新试探点. 线搜索中我们采取回溯的策略, 而在信赖域算法中我们减小信赖域的半径重新计算新的$p$. 我们也会拒绝过于靠近信赖域边界的$x+p_x$, 毕竟这样会大大增加价值函数中的障碍项$-\mu {\sum }_{i\in \mathcal{I}}\log (s_i)$.

4. 线搜索内点法

我们现在给出对线搜索内点法更加详尽的描述. 我们以$D{\varphi }_v(x,s;p)$表示价值函数${\varphi }_v$在$(x,s)$处对方向$p$的方向导数. 停机准则则基于之前定义的误差函数$E$.

算法3 (Line Search Interior-Point Algorithm)
Choose $x_0$ and $s_0>0$, and compute initial values for the multipliers $y_0$ and $z_0>0$. If a quasi-Newton approach is used, choose an $n\times n$ symmetric and positive definite initial matrix $B_0$. Select an initial barrier parameter $\mu >0$, parameters $\eta ,\sigma \in (0,1)$, and tolerances ${ϵ}_{\mu }$ and ${ϵ}_{tol}$. Set $k\leftarrow 0$.
repeat until $E(x_k,s_k,y_k,z_k;0)\le {ϵ}_{tol}$
\quad\quad repeat until $E(x_k,s_k,y_k,z_k;\mu )\le {ϵ}_{\mu }$
\quad\quad\quad\quad Compute the primal-dual direction $p=(p_x,p_s,p_y,p_z)$ from primal-dual system, where the coefficient matrix is modified if necessary;
\quad\quad\quad\quad Compute ${\alpha }_s^{\max },{\alpha }_z^{\max }$; Set $p_w=(p_x,p_s)$;
\quad\quad\quad\quad Compute step lengths ${\alpha }_s,{\alpha }_z$ satisfying $${\varphi }_v(x_k+{\alpha }_s{p}_x,s_k+{\alpha }_s{p}_s)\le {\varphi }_v(x_k,s_k)+\eta {\alpha }_{s}D{\varphi }_v(x_k,s_k;p_w);$$ \quad\quad\quad\quad Compute $(x_{k+1},s_{k+1},y_{k+1},z_{k+1})$;
\quad\quad\quad\quad if a quasi-Newton approach is used
\quad\quad\quad\quad\quad\quad update the approximation $B_k$;
\quad\quad\quad\quad Set $k\leftarrow k+1$;
\quad\quad end
\quad\quad Set $\mu \leftarrow \sigma \mu$ and update ${ϵ}_{\mu }$;
end

障碍容忍限可以定义成如算法1中的${ϵ}_{\mu }=\mu$. 此算法框架中我们可以方便地使用自适应更新障碍因子$\mu$的策略. 若价值函数可能会引发Maratos效应, 则需要做二阶校正或采取非单调策略. 我们还可以用滤子替代价值函数.

我们在第7节会看到, 算法3必须加上防护措施才能保证有全局收敛性.

5. 信赖域内点法

我们现在考虑使用信赖域增强收敛性的内点法. 正如在无约束情形中, 信赖域框架给予了Hessian选取很大的自由度, 并且提供了一种处理Jacobi阵和Hessian阵奇异的机制. 当然为此我们需要比线搜索更复杂的迭代过程.

下面要介绍的内点法渐进等价于第4节中的线搜索内点法, 但在两个方面与之有较大的不同. 首先前者不完全是原始-对偶算法, 因为它会先计算变量$(x,s)$的迭代步, 再对乘子做更新. 其次, 信赖域算法使用对变量做了尺度变换, 使变量不会跑向可行域的边界. 这使得算法产生的迭代步与线搜索的不同, 且具有更好的收敛性质.

我们首先给出近似求解一个固定障碍问题的信赖域算法. 之后再给出完整的算法.

5.1 求解障碍问题的算法

障碍问题是等式约束的问题, 可用带信赖域约束的SQP求解. 然而直接对障碍问题使用SQP会得到违反松弛变量正约束的迭代步, 且迭代步还会频繁地被信赖域约束截断. 为克服此困难, 我们设计一种针对障碍问题特殊结构的SQP算法.

在$(x,s)$处, 对给定的障碍因子$\mu$, 我们首先计算Lagrang乘子估计$(y,z)$, 再计算近似求解以下子问题的$p=(p_x,p_s)$:$$\begin{array}{rl}\underset{p_x,p_s}{\min }& \nabla f^T{p}_x+\frac{1}{2}{p}_x^T{\nabla }_{xx}^2\mathcal{L}{p}_x-\mu e^T{S}^{-1}{p}_s+\frac{1}{2}{p}_s^T\Sigma p_s\\ \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& A_E(x)p_x+c_E(x)=r_E,\\ & A_I(x)p_x-p_s+(c_I(x)-s)=r_I,\\ & \Vert (p_x,S^{-1}{p}_s){\Vert }_2\le \Delta ,\\ & p_s\ge -\tau s.\end{array}$$这里$\Sigma$为原始-对偶阵中的子块, 标量$\tau \in (0,1)$靠近1(如0.995). 不等式约束$p_s\ge -\tau s$的作用与分数到边准则相同. 理想状态下, 我们希望设$r=(r_E,r_I)=0$, 但这可能会使得约束不相容或是减少可行性上可以获得的改进. 因此我们额外地需要再计算$r$. 可见第十八章算法4.

注意目标函数的选取是基于这样一个事实: 上述子问题前三行的KKT条件与原非线性规划的相同(互补条件差一个尺度变换$S^{-1}$). 因此子问题得到的迭代步与原始-对偶线搜索的关系就像是SQP和第十八章第1节Newton-Lagrange步的关系.
信赖域的约束保证了即使${\nabla }_{xx}^2\mathcal{L}(x,s,y,z)$不是正定的, 问题也有有限的解, 因此Hessian阵不需要修改. 另外, 信赖域的构造保证了每一次迭代都有一定的改进. 因为信赖域的形状必须考虑不让松弛变量过早接近0, 所以约束中使用了$S^{-1}$. 这样就限制了$s$中靠近下界0的分量对应的$p_s$. 下面我们还会看到, 这对松弛向量$r_E,r_I$的选取也有重要作用.

我们给出信赖域SQP算法的大概描述. 停机准则以误差函数$E$定义, 价值函数${\varphi }_v$可用之前的, 使用2-范数.

算法4 (Trust-Region Algorithm for Barrier Problems)
Input parameters: $\mu >0,x_0,s_0>0,{ϵ}_{\mu }$, and ${\Delta }_0>0$. Compute Lagrange multiplier estimates $y_0$ and $z_0>0$. Set $k\leftarrow 0$.
repeat until $E(x_k,s_k,y_k,z_k;\mu )\le {ϵ}_{\mu }$
\quad\quad Compute $p=(p_x,p_s)$ by approximately solving subproblem.
\quad\quad if $p$ provides sufficient decrease in the merit function ${\varphi }_v$
\quad\quad\quad\quad Set $x_{k+1}\leftarrow x_k+p_x,s_{k+1}\leftarrow s_k+p_s$;
\quad\quad\quad\quad Compute new multiplier estimates $y_{k+1},z_{k+1}>0$ and set ${\Delta }_{k+1}\ge {\Delta }_k$;
\quad\quad else
\quad\quad\quad\quad Define $x_{k+1}\leftarrow x_k,s_{k+1}\leftarrow s_k$, and set ${\Delta }_{k+1}<{\Delta }_k$;
\quad\quad end
\quad\quad Set $k\leftarrow k+1$;
end (repeat))

算法4用于固定的$\mu$. 而完整的内点法算法则需要 { μ k } → 0 \{\mu_k\}\to0 {μk​}→0. 首先我们讨论如何近似求解子问题, 以及如何计算Lagrange乘子估计$(y_{k+1},z_{k+1})$.

5.2 迭代步的计算

因为有非线性约束和下界的存在, 子问题是很难精确求解的. 但我们可以以适当的计算量计算有用的精确解. 由于此法对变量和约束的个数不敏感, 因此这提供了一种大规模情形的实用内点法框架.

首先我们要做变量替换, 使信赖域约束变成球状. 定义$$\tilde{p}=\left[\begin{array}{c}{p}_x\\ {\tilde{p}}_s\end{array}\right]=\left[\begin{array}{c}{p}_x\\ S^{-1}{p}_s\end{array}\right],$$我们可以将子问题写成$$\begin{array}{rl}\underset{p_x,{\tilde{p}}_s}{\min }& \nabla f^T{p}_x+\frac{1}{2}{p}_x^T{\nabla }_{xx}^2\mathcal{L}{p}_x-\mu e^T{\tilde{p}}_s+\frac{1}{2}{\tilde{p}}_s^{T}S\Sigma S{\tilde{p}}_s\\ \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& A_E(x)p_x+c_E(x)=r_E,\\ & A_I(x)p_x-S{\tilde{p}}_s+(c_I(x)-s)=r_I,\\ & \Vert (p_x,{\tilde{p}}_s){\Vert }_2\le \Delta ,\\ & {\tilde{p}}_s\ge -\tau e.\end{array}$$为计算$r_E,r_I$, 我们按第十八章第5节中的策略, 构造附加子问题:$$\begin{array}{rl}\underset{v}{\min }& \Vert A_E(x)v_x+c_E(x){\Vert }_2^2+\Vert A_I(x)v_x-S{v}_s+(c_I(x)-s){\Vert }_2^2\\ \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& \Vert (v_x,v_s){\Vert }_2\le 0.5\Delta ,\\ & v_s\ge -(\tau /2)e.\end{array}$$如果我们忽略下界约束, 则这就是个标准的信赖域问题, 我们可用第四章的技术求解. 如果解违反了下界约束, 就进行回溯. 我们不需要精确地求解这个附加子问题, 我们只需要$r_E,r_I$对于约束是可行的.

求解完附加子问题后, 定义$$r_E=A_E(x)v_x+c_E(x),r_I=A_I(x)v_x-S{v}_s+(c_I(x)-s).$$现在近似求解子问题得到$\tilde{d}$. 由$r_E,r_I$的定义, $v$是等式线性约束的特解. 我们可以用投影CG求解等式约束的二次规划, 而用Steihaug的策略停止迭代: 在CG迭代的过程中, 检测信赖域约束, 若此约束被打破或是遇到了负曲率, 亦或是求得了近似解, 就停止. 若由投影CG得到的解不满足${\tilde{p}}_s\ge -\tau e$, 我们就做回溯直到它满足. 计算完$(p_x,{\tilde{p}}_s)$后, 再变换回去得到$p$.

每步投影CG迭代都需要求解线性系统. 对于等式约束的子问题, 投影矩阵为$$\left[\begin{array}{cc}I& {\hat{A}}^T\\ \hat{A}& O\end{array}\right],\hat{A}=\left[\begin{array}{cc}{A}_E(x)& O\\ A_I(x)& -S\end{array}\right].$$因此尽管此信赖域方法仍然需要求解增广系统, 但这里的系数矩阵要比原始-对偶矩阵简单. 特别地, 我们不需要去分解Hessian阵${\nabla }_{xx}^2\mathcal{L}$, 因为CG仅需要矩阵-向量乘积.

我们在第3节提到$S\Sigma S$的特征值分布要比$\Sigma$更紧凑. 因此, CG通常不会被病态所影响, 从而是求解子问题二次规划的可行方法.

5.3 Lagrange乘子估计和步长接收

在迭代点$(x,s)$处, 我们选取$(y,z)$为最小二乘乘子估计:$$\left[\begin{array}{c}y\\ z\end{array}\right]={\left(\hat{A}{\hat{A}}^T\right)}^{-1}\hat{A}\left[\begin{array}{c}\nabla f(x)\\ -\mu e\end{array}\right].$$这样估计得到的$z$可能不总是正的. 为此, 我们重新定义负的分量为$$z_i\leftarrow \min (10^{-3},\mu /s_i),i=1,2,\dots ,m.$$这里$\mu /s_i$称作是第$i$个原始乘子估计, 因为若所有的$z$的分量都用上述式子定义, 则$\Sigma$就变成了原始模式下的$\Sigma$.

与标准信赖域方法相同, $p$被接收若$$\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{d}(p)\ge \eta \mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}(p),$$其中$$\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{d}(p)={\varphi }_v(x,s)-{\varphi }_v(x+p_x,s+p_s),$$$\eta$为$(0,1)$中的常数(比如$\eta =10^{-8}$). 预测下降量为$$\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}(p)=q_v(0)-q_v(p),$$其中$$q_v(p)=\nabla f^T{p}_x+\frac{1}{2}{p}_x^T{\nabla }_{xx}^2\mathcal{L}{p}_x-\mu e^T{S}^{-1}{p}_s+\frac{1}{2}{p}_s^T\Sigma p_s+vm(p),$$$$m(p)={\Vert \left[\begin{array}{c}{A}_E(x)p_x+c_E(x)\\ A_I(x)p_x-p_s+c_I(x)-s\end{array}\right]\Vert }_2.$$为确定惩罚因子$v$的值, 我们要求$v$充分大使得$$\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}(p)\ge \rho v(m(0)-m(p)),\rho \in (0,1).$$这与第十八章中相同.

5.4 信赖域内点法

现在我们给出求解非线性规划问题信赖域内点法更加详尽的描述. 我们采用Fiacco-McCormick策略更新障碍因子. 停机准则依然考虑误差函数$E$. 若使用拟牛顿算法, Hessian阵${\nabla }_{xx}^2\mathcal{L}$就用一对称矩阵近似.

算法5 (Trust-Region Interior-Point Algorithm)
Choose a value for the parameters $\eta >0,\tau \in (0,1),\sigma \in (0,1),$ and $\zeta \in (0,1)$, and select the stopping telerances ${ϵ}_{\mu },{ϵ}_{tol}$. If a quasi-Newton approach is used, select an $n\times n$ symmetric initial matrix $B_0$. Choose initial values for $\mu >0,x_0,s_0>0$, and ${\Delta }_0$. Set $k\leftarrow 0$.
repeat until $E(x_k,s_k,y_k,z_k;0)\le {ϵ}_{tol}$
\quad\quad repeat until $E(x_k,s_k,y_k,z_k;\mu )\le {ϵ}_{\mu }$
\quad\quad\quad\quad Compute Lagrange multipliers by least-squares;
\quad\quad\quad\quad Compute ${\nabla }_{xx}^2\mathcal{L}(x_k,s_k,y_k,z_k)$ or update a quasi-Newton approximation $B_k$, and define ${\Sigma }_k$;
\quad\quad\quad\quad Compute the normal step $v_k=(v_x,v_s)$;
\quad\quad\quad\quad Compute ${\tilde{p}}_k$ by applying the projected CG method to the subproblem;
\quad\quad\quad\quad Obtain the total step $p_k$;
\quad\quad\quad\quad Update $v_k$;
\quad\quad\quad\quad Compute ${\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}_k(p_k),{\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{d}}_k(p_k)$;
\quad\quad\quad\quad if ${\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{d}}_k(p_k)\ge \eta {\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}_k(p_k)$
\quad\quad\quad\quad\quad\quad Set $x_{k+1}\leftarrow x_k+p_x,s_{k+1}\leftarrow s_k+p_s$;
\quad\quad\quad\quad\quad\quad Choose ${\Delta }_{k+1}\ge {\Delta }_k$;
\quad\quad\quad\quad else
\quad\quad\quad\quad\quad\quad Set $x_{k+1}=x_k,s_{k+1}=s_k$; and choose ${\Delta }_{k+1}<{\Delta }_k$;
\quad\quad\quad\quad end (if)
\quad\quad\quad\quad Set $k\leftarrow k+1$;
\quad\quad end
\quad\quad Set $\mu \leftarrow \sigma \mu$ and update ${ϵ}_{\mu }$;
end

为避免Maratos效应, 我们可以选择性地加入二阶校正. 障碍因子的更新也可采用自适应的策略.

6. 原始对数障碍函数法

在原始-对偶内点法之前, 障碍函数法是在原始变量$x$的空间上运行的. 如同第十七章中的二次罚函数法, 这里的目标是要通过求解一系列无约束极小来求解非线性规划问题.

原始障碍函数法在不等式约束问题中更好表述:$$\underset{x}{\min }f(x),\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}c(x)\ge 0.$$
对数障碍函数则定义为$$P(x;\mu )=f(x)-\mu \sum _{i\in \mathcal{I}}\log c_i(x),$$其中$\mu >0$. 我们可以证明在一定条件下, $P(x;\mu )$的极小点$x(\mu )$在$\mu \downarrow 0$时趋近解. 轨迹${\mathcal{C}}_p$定义为 C p = d e f { x ( μ ) ∣ μ > 0 } , \mathcal C_p\xlongequal{def}\{x(\mu)\mid \mu>0\}, Cp​def {x(μ)∣μ>0},称为原始中心路径(primal central path).

由于$x(\mu )$严格落在可行集 { x ∣ c ( x ) > 0 } \{x\mid c(x)>0\} {x∣c(x)>0}中, 原则上我们可以用任何一种无约束极小的算法求之. 但这些都需要一定的修正, 从而能够拒绝离开可行集边界或靠近边界的迭代步.

一种求Lagrange乘子估计的方法基于对$P$的求导:$${\nabla }_{x}P(x;\mu )=\nabla f(x)-\sum _{i\in \mathcal{I}}\frac{\mu }{c_i(x)}\nabla c_i(x).$$当$x$靠近$x(\mu )$且$\mu$很小时, 最优Lagrange乘子$z_i^{\ast },i\in \mathcal{I}$就可如下估计:$$z_i^{\ast }\approx \mu /c_i(x),i\in \mathcal{I}.$$一种基于原始对数障碍函数的一般算法框架如下.

框架6 (Unconstrained Primal Barrier Method)
Given ${\mu }_0>0$, a sequence { τ k } \{\tau_k\} {τk​} with ${\tau }_k\to 0$, and a starting point $x_0^s$;
for $k=0,1,2,\dots$
\quad\quad Find an approximate minimizer $x_k$ of $P(\cdot ;{\mu }_k)$, starting at $x_k^s$, and terminating when $\Vert \nabla P(x_k;{\mu }_k)\Vert \le {\tau }_k$;
\quad\quad Compute Lagrange multipliers $z_k$;
\quad\quad if final convergence test satisfied
\quad\quad\quad\quad stop with approximate solution $x_k$;
\quad\quad Choose new penalty parameter ${\mu }_{k+1}<{\mu }_k$;
\quad\quad Choose new starting point $x_{k+1}^s$;
end (for)

原始障碍函数法由Frisch在上世纪五十年代首次提出, 由Fiacco和McCormick在六十年代末分析与推广. 在SQP算法引入后它便淡出了人们的视线, 且由于比之原始-对偶内点法, 它具有诸多缺陷, 于是它再也没有重得重视. 这里最大的缺陷就是$x(\mu )$在$\mu \downarrow 0$时由于$P(x;\mu )$的非线性性变得越来越难求得.

例1 考虑问题$$\min (x_1+0.5{)}^2+(x_2-0.5{)}^2,\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}{x}_1\in [0,1],x_2\in [0,1],$$此时原始障碍函数为$$P(x;\mu )=(x_1+0.5{)}^2+(x_2-0.5{)}^2-\mu [\log x_1+\log (1-x_1)+\log x_2+\log (1-x_2)].$$次函数在$\mu =0.01$时的等高线如下图所示.

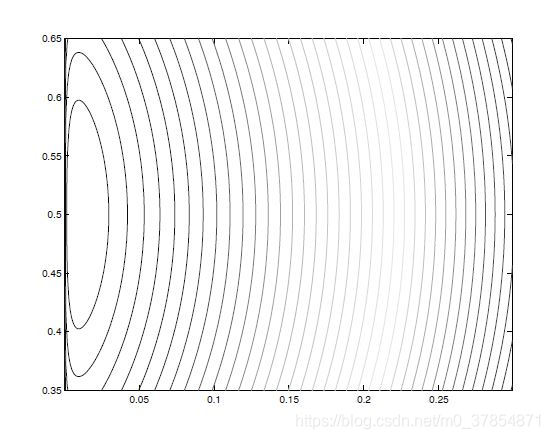
细长的等高线表明问题较为病态, 这使得一些无约束优化的算法表现不好, 比如拟牛顿法、最速下降法和共轭梯度法. 牛顿法对于尺度变换不敏感, 但图中的等高线显然不好用二次模型近似. 这就使得牛顿步不能很好得抓住障碍函数的特质. 因此除非在解的一个小邻域内, 否则牛顿法的收敛速度也不会很快.

为减缓非线性性带来的影响, 我们可以仿照第十七章的做法, 引入额外的变量. 定义$z_i=\mu /c_i(x)$, 我们就可以将稳定性条件重新写作$$\begin{array}{rl}\nabla f(x)-\sum _{i\in \mathcal{I}}{z}_i\nabla c_i(x)& =0,\\ C(x)z-\mu e& =0,\end{array}$$其中$C(x)=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(c_1(x),c_2(x),\dots ,c_m(x))$. 注意若我们再额外添加松弛变量, 此系统就等价于扰动KKT条件. 最终若对变量$(x,s,z)$使用牛顿法, 并暂时忽略$s,z\ge 0$, 我们就得到了原始-对偶的构造. 因此事后看来, 我们可以将原始对数障碍函数法转变成原始-对偶线搜索算法或是信赖域算法.

经典的原始障碍函数法的其他缺陷为, 它需要一可行的初始点, 而这在许多情形下是很难得到的. 同时将等式约束包含进原始函数中也比较成问题. 如果采用二次罚项, 则又会有与二次惩罚函数类似的问题.

多年来, 原始障碍函数法的缺陷被归结为$P$的病态Hessian阵. 注意到$${\nabla }_{xx}^{2}P(x;\mu )={\nabla }^{2}f(x)-\sum _{i\in \mathcal{I}}\frac{\mu }{c_i(x)}{\nabla }^2{c}_i(x)+\sum _{i\in \mathcal{I}}\frac{\mu }{c_i^2(x)}\nabla c_i(x)\nabla c_i(x{)}^T.$$将乘子的估计代入并利用Lagrange函数$\mathcal{L}(x,z)$的定义, 我们有$${\nabla }_{xx}^{2}P(x;\mu )\approx {\nabla }_{xx}^2\mathcal{L}(x,z^{\ast })+\sum _{i\in \mathcal{I}}\frac{1}{\mu }(z_i^{\ast }{)}^2\nabla c_i(x)\nabla c_i(x{)}^T.$$这与二次罚函数的Hessian比较相似. 类似地对${\nabla }_{xx}^{2}P(x;\mu )$进行分析也会发现它在解$x(\mu )$附近随着$\mu$趋于0时会愈发病态.

这种病态会对最速下降法、共轭梯度法或是拟牛顿法的效率造成毁灭性的影响. 因此将这些无约束算法造成的问题归结为病态时正确的. 但牛顿法则是不受尺度影响的, 但它的表现仍然不尽人意. 如上面解释的,此时$P$的高度非线性性会给牛顿法造成巨大的困难.

7. 全局收敛性质

我们现在讨论原始-对偶内点法的一些全局收敛性质. 定理1是分析的开端. 它给出了由内点法产生的迭代点的聚点时非线性问题的KKT点的条件. 定理1假设对每个${\mu }_k$, 扰动KKT条件都(在一定精度下)被满足. 本节我们就讨论在什么情况下这样的假设时成立的.

我们首先给出一个令人惊叹的事实. 尽管线搜索原始-对偶算法是线性和二次规划全局收敛的内点法的基础, 但在非线性规划中(即使是在非退化的问题上)它并不保证有效.

7.1 线搜索方法的失效

我们在第十一章说到, 当Jacobi阵亏秩时, 非线性方程的牛顿迭代可能会失效. 我们现在讨论内点法的例子. 具体说来, 失效的原因是没有很好地协调步长计算和界的控制.

例2 考虑问题$$\begin{array}{rl}\min & x\\ \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& c_1(x)-s\stackrel{def}{=}{x}^2-s_1-1=0,\\ & c_2(x)-s\stackrel{def}{=}x-s_2-\frac{1}{2}=0,\\ & s_1\ge 0,s_2\ge 0.\end{array}$$注意不等式约束对$(x,s)$的Jacobi处处是满秩的. 我们使用线搜索内点法, 从初始点$x^{(0)}$出发, 满足$(s_1^{(0)},s_2^{(0)})>0,c_1(x^{(0)})-s^{(0)}\ge 0$. 下图在$x-s_1$平面上形象地表现了可行域和初始点.

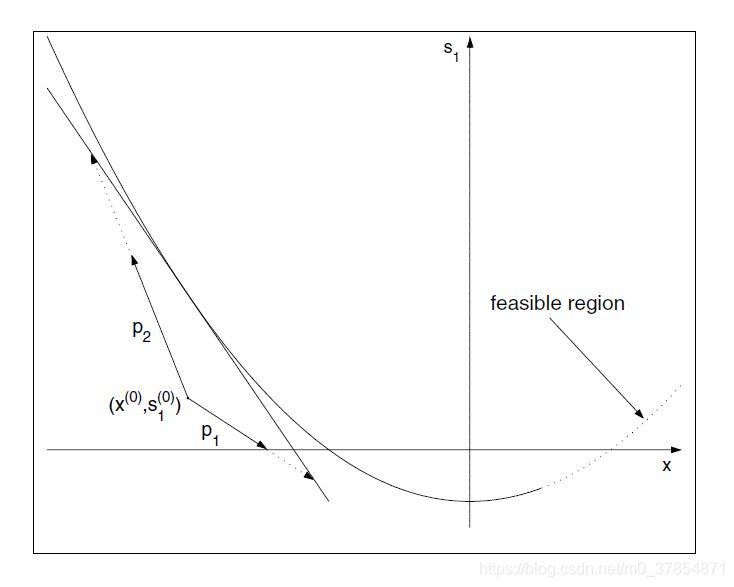
满足线性化约束的原始-对偶步会从$x^{(0)}$出发走向抛物线的切线. 图中$p_1,p_2$是满足线性化约束的可能的迭代步. 因此性的迭代点$x^{(1)}$位于$x^{(0)}$和切线之间. 但由于$s_1$必须保持为正, $x^{(1)}$会位于横轴的上方. 因此从 { ( x , s 1 , s 2 ) : x 2 − s 1 − 1 ≥ 0 , s 1 ≥ 0 } \{(x,s_1,s_2):x^2-s_1-1\ge0,s_1\ge0\} {(x,s1​,s2​):x2−s1​−1≥0,s1​≥0}的任何初始点出发, 下一个迭代点都依然在这个区域. 因此 { x ( k ) } \{x^{(k)}\} {x(k)}将永远不会离开此区域, 从而永远不会成为可行点.

这种潜在的收敛还会影响许多产生满足线性化约束方向, 且强制分数到边准则的算法. 价值函数仅能限制步长过长, 无力解决此困境. 而更新$\mu$的策略也无济于事, 因为以上仅用到了线性化的约束.

上例对区域中所有的初始点, 内点法都收敛到$(-\beta ,0,0),\beta >0$. 换句话说, 算法可能收敛到 { ( x , s 1 , s 2 ) : s 1 ≥ 0 , s 2 ≥ 0 } \{(x,s_1,s_2):s_1\ge0,s_2\ge0\} {(x,s1​,s2​):s1​≥0,s2​≥0}边界上的一个不可行、非最优(实际上对于可行性度量也非稳定)的点. 这一点障碍函数法可以避免.

此类例子在实际中很少见, 但这表明了从KKT入手是存在理论缺陷的. 这不一定会表现在收敛失效, 更多地可能是在收敛不是那么地高效.

7.2 修正线搜索方法

为克服这一问题, 处理由Hessian和Jacobi阵奇异性带来的困难, 我们必须在某些情形下修改线搜索内点法的搜索方向. 一种方式是惩罚约束. 这样的惩罚-障碍函数法仅在最近提出, 还没有成熟的实施规则.

在实际中应用地较为成功的一种方式是控制步长${\alpha }_s,{\alpha }_z$. 若它们小于给定的阈值, 就不取原始-对偶步, 而是取一步保证能够提升可行性(若可以, 提升最优性). 在滤子法中, 当步长很小时, 我们可以调用可行性恢复阶段, 从而在下一迭代点提升可行性. 一种不同方式则是转而使用信赖域算法, 以信赖域迭代步(算法5)代替原始-对偶步.

以上这些是有理论依据的, 这是因为当线搜索迭代收敛于非稳定点时, 步长${\alpha }_s,{\alpha }_z$将会收敛于0. 从实用的角度来看, 此策略就不总是令人满意. 因为它是在不良迭代步产生后才反应, 而不是直接阻止这样迭代步的产生. 同时, 我们也需要启发式的方法判断步长是否过小. 不过, 下面我们要讨论的信赖域框架, 就总是产生良好的迭代步, 而不需要防护措施.

7.3 信赖域算法的全局收敛性

算法5中的信赖域内点法有良好的全局收敛性. 为说明简单, 我们以不等式约束问题为例分析. 我们先考虑对固定$\mu$的障碍问题的解, 之后再看整个算法.

以下, $B_k$表示Hessian阵${\nabla }_{xx}^2{\mathcal{L}}_k$或一拟牛顿近似矩阵. 不可行性度量$h(x)=\Vert [c(x){]}^{-}\Vert$, 其中 [ y ] = max ⁡ { 0 , − y } [y]=\max\{0,-y\} [y]=max{0,−y}. 此度量为0当且仅当$x$为可行点. 注意$h(x{)}^2$可微, 其梯度为$$\nabla [h(x{)}^2]=2A(x)c(x{)}^{-1}.$$我们说序列 { x k } \{x_k\} {xk​}渐进可行, 若$c(x_k{)}^{-}\to 0$.

定理2 设算法5用于障碍问题, $\mu$固定, 内循环${ϵ}_{\mu }=0$. 假设序列 { f k } \{f_k\} {fk​}下有界且序列 { ∇ f k } , { c k } , { A k } , { B k } \{\nabla f_k\},\{c_k\},\{A_k\},\{B_k\} {∇fk​},{ck​},{Ak​},{Bk​}有界. 则下面三种情形必有一个发生:

1. 序列 { x k } \{x_k\} {xk​}不渐进可行. 此时迭代点趋于不可行性度量$h(x)=\Vert c(x{)}^{-}\Vert$的稳定点, 这意味着$A_k{c}_k^{-}\to 0$, 惩罚因子$v_k\to \infty$.
2. 序列 { x k } \{x_k\} {xk​}渐进可行, 但序列 { ( c k , A k ) } \{(c_k,A_k)\} {(ck​,Ak​)}有聚点$(\bar{\gamma },\bar{A})$不满足LICQ. 此时也有惩罚因子$v_k\to \infty$.
3. 序列 { x k } \{x_k\} {xk​}渐进可行, 且 { ( c k , A k ) } \{(c_k,A_k)\} {(ck​,Ak​)}的所有聚点都满足LICQ. 此时对充分大的$k$, 惩罚因子$v_k$为常数, $c_k>0$. 聚点还满足障碍问题的稳定性条件.

此定理的证明可见Byrd R H, Gilbert J C, Nocedal J². 此定理给出了KKT条件可能在聚点处不满足的两种情形. 第一种情形中, 在聚点处没有方向可以在一阶上改进可行性. 这种情形是可能的, 这是因为如果没有好的初始点, 局部方法不总是能找到问题的可行点. 第二种情形中, 我们必须记住在某些情形下, 问题的解处不一定有LICQ从而此解不是KKT点. 第三种情形则是我们最想得到的情形. 在实际中, 我们可以通过比如观察惩罚因子$v_k$来控制这种情形.

下面讨论将算法5的完整算法应用到非线性规划问题中. 结合定理1和定理2, 我们知道有以下几种情形可能会发生:

• 对算法产生的某个障碍因子$\mu$, 要么不等式$\Vert c_k-s_k\Vert \le {ϵ}_{\mu }$永远不成立, 此时在极限点是$h(x)$的稳定点, 要么$(c_k-s_k)\to 0$, 此时 { ( c k , A k ) } \{(c_k,A_k)\} {(ck​,Ak​)}有极限点$(\bar{c},\bar{A})$, 不满足LICQ;
• 在算法5的每一次外循环中, 内循环退出准则$E(x_k,s_k,y_k,z_k;\mu )\le {ϵ}_{\mu }$总会成立. 于是迭代点列的所有聚点都是可行的. 进一步, 若有聚点$\hat{x}$满足LICQ, 则$\hat{x}$为非线性规划的KKT点.

8. 超线性收敛性

我们可以使原始-对偶内点法在解附近快速地收敛. 我们只需要仔细地控制障碍因子$\mu$和内循环收敛容忍限${ϵ}_{\mu }$的下降, 并令$\tau$充分快地收敛到1. 下面我们给出在线搜索迭代中更新这些参数的策略. 这些策略可以方便地扩展到信赖域的框架.

以下我们假设价值函数或滤子是不积极的. 这一假设是现实的, 因为只要小心地实施算法(可能需要二阶校正步或其他的一些策略), 我们就能保证在解附近, 由原始-对偶算法产生的所有迭代点都能被价值函数或滤子所接受.

我们表示原始-对偶迭代点为$$v=(x,s,y,z)$$并定义满原始-对偶步(无回溯)为$$v^{+}=v+p,$$其中$p$为KKT方程的解. 为构建局部收敛理论, 我们假设迭代点收敛到一个满足一定正则性假设的解.

假设1

1. $v^{\ast }$为非线性规划的解, 其满足KKT条件.
2. Hessian阵${\nabla }^{2}f(x),{\nabla }^2{c}_i(x),i\in \mathcal{E}\cup \mathcal{I}$在$v^{\ast }$局部Lipschitz连续.
3. $v^{\ast }$满足LICQ、严格互补松弛条件、二阶充分性条件.

我们假设$v$为满足内循环终止条件$E(v,\mu )\le {ϵ}_{\mu }$的点, 障碍因子由$\mu$减少到${\mu }^{+}$. 我们现在讨论如何控制算法3中的参数, 使得以下三个性质在$v^{\ast }$的一邻域成立:

1. 迭代点$v^{+}$满足分数到边准则, 即${\alpha }_s^{\max }={\alpha }_z^{\max }=1$.
2. $v^{+}$满足内循环终止条件, 即$E(v^{+};{\mu }^{+})\le {ϵ}_{{\mu }^{+}}$.
3. 迭代点列超线性收敛于$v^{\ast }$.

我们可以令$${ϵ}_{\mu }=\theta \mu ,{ϵ}_{{\mu }^{+}}=\theta {\mu }^{+},$$其中$\theta >0$, 且设置其他的参数为$${\mu }^{+}={\mu }^{1+\delta },\delta \in (0,1);\tau =1-{\mu }^{\beta },\beta >\delta .$$当然也有其他的控制参数的方式. 例如, 我们可能更想由KKT条件的满足度(如$E$)决定$\mu$的改变. 以上三条可证明在${ϵ}_{\mu }$如上定义, 且以$E(v;0)$替换上面定义${\mu }^{+},\tau$的$\mu$时, 是成立的.

要满足第二条, $\mu$的下降速度是有限度的. 我们可以证明$\mu$不可以快于二次的速度下降, 因为总体的收敛速度不可能快于二次. 自然, 当$\tau$为常数, ${\mu }^{+}=\sigma \mu ,\sigma \in (0,1)$时, 内点法仅为线性收敛.

尽管超线性收敛很好, 但这种收敛往往仅在迭代的最后几步可以观察到.

10. 关于内点法的进一步讨论

一方面, 内点法在大规模的问题上具有优势. 它们在这种问题上往往(但不总是)比积极集法要好. 内点法需要在每次迭代求解一个线性系统, 而此系统的矩阵结构是不变的. 因此我们可以考量这一结构, 设计更好的算法. 直接分解技术和投影CG都是可行的, 这给用户求解问题的自由度带来了许多便利.

另一方面, 内点法不如积极集法, 前者需要在每次迭代考虑所有的约束. 因此原始-对偶迭代在某些问题上可能耗费过大.

内点法的主要缺陷之一是, 它们对于初始点的选取、问题的尺度以及障碍因子$\mu$的更新策略特别敏感. 若迭代点过早地接近了可行域的边界, 内点法就不太容易脱离, 收敛就会比较慢. 不过, 自适应的更新$\mu$的策略已经开始缓解这种敏感性了, 未来将有希望得到更多鲁棒的结果.

---

1. A.V. Fiacco and G.P. McCormick, Nonlinear Programming:Sequential Unconstrained Minimization Techniques, John Wiley & Sons, New York, N.Y., 1968. Reprinted by SIAM Publications, 1990. ↩︎

2. Byrd R H, Gilbert J C, Nocedal J. A Trust Region Method Based on Interior Point Techniques for Nonlinear Programming[J]. 1998. ↩︎