机器学习之学习曲线learning curve和过拟合、欠拟合

最新推荐文章于 2025-02-23 09:05:29 发布

a flying bird

最新推荐文章于 2025-02-23 09:05:29 发布

阅读量1.8w

点赞数 13

分类专栏：机器学习

本文链接：https://blog.csdn.net/m0_37870649/article/details/79810542

版权

机器学习专栏收录该内容

31 篇文章

订阅专栏

本文介绍了学习曲线的概念及如何通过学习曲线判断模型的欠拟合与过拟合状态，并提出了包括正则化、数据增强在内的多种解决过拟合问题的方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、学习曲线

学习曲线是什么？

学习曲线就是通过画出不同训练集大小时训练集和交叉验证的准确率，可以看到模型在新数据上的表现，进而来判断模型是否方差偏高或偏差过高，以及增大训练集是否可以减小过拟合。

怎么解读？

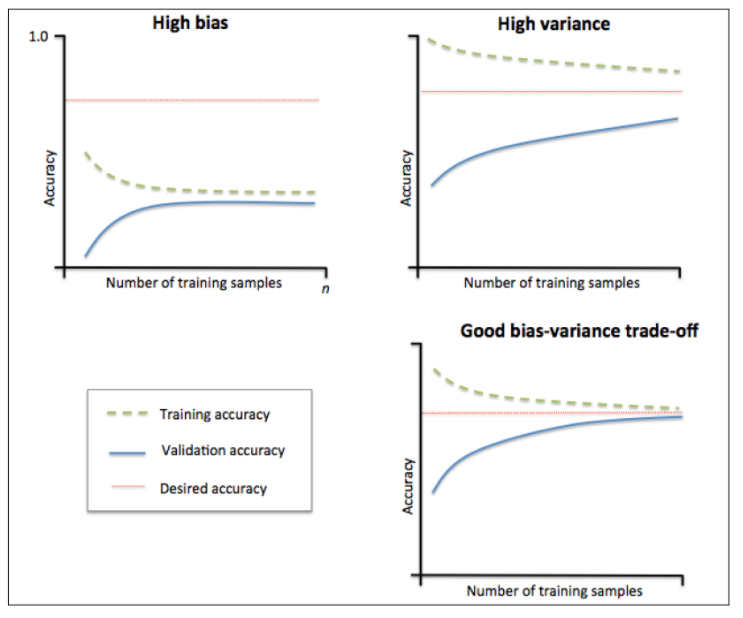
当训练集和测试集的误差收敛但却很高时，为高偏差。
左上角的偏差很高，训练集和验证集的准确率都很低，很可能是欠拟合。
我们可以增加模型参数，比如，构建更多的特征，减小正则项。
此时通过增加数据量是不起作用的。

当训练集和测试集的误差之间有大的差距时，为高方差。
当训练集的准确率比其他独立数据集上的测试结果的准确率要高时，一般都是过拟合。
右上角方差很高，训练集和验证集的准确率相差太多，应该是过拟合。
我们可以增大训练集，降低模型复杂度，增大正则项，或者通过特征选择减少特征数。

理想情况是是找到偏差和方差都很小的情况，即收敛且误差较小。

函数接口是什么?

参数说明：rain_sizes, train_scores, test_scores = learning_curve(）

输入：
(estimator : 你用的分类器。
title : 表格的标题。
X : 输入的feature，numpy类型
y : 输入的target vector
ylim : tuple格式的(ymin, ymax), 设定图像中纵坐标的最低点和最高点
cv : 做cross-validation的时候，数据分成的份数，其中一份作为cv集，其余n-1份作为training(默认为3份)
n_jobs : 并行的的任务数(默认1))
输出：(train_sizes_abs :训练样本数
train_scores:训练集上准确率
test_scores:交叉验证集上的准确率)

怎么画？

实例1：

在画学习曲线时，横轴为训练样本的数量，纵轴为准确率。

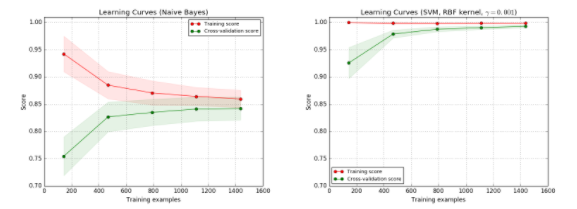
例如同样的问题，左图为我们用 naive Bayes 分类器时，效果不太好，分数大约收敛在 0.85，此时增加数据对效果没有帮助。

右图为 SVM（RBF kernel），训练集的准确率很高，验证集的也随着数据量增加而增加，不过因为训练集的还是高于验证集的，有点过拟合，所以还是需要增加数据量，这时增加数据会对效果有帮助。

上图的代码如下：

模型这里用 GaussianNB 和 SVC 做比较，
模型选择方法中需要用到 learning_curve 和交叉验证方法 ShuffleSplit。

import numpy as np
import matplotlib.pyplot as plt

from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC

from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit

首先定义画出学习曲线的方法，
核心就是调用了 sklearn.model_selection 的 learning_curve，
学习曲线返回的是 train_sizes, train_scores, test_scores，
画训练集的曲线时，横轴为 train_sizes, 纵轴为 train_scores_mean，
画测试集的曲线时，横轴为 train_sizes, 纵轴为 test_scores_mean：

def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
                        n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
    ~~~
    train_sizes, train_scores, test_scores = learning_curve(
        estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
    train_scores_mean = np.mean(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)  
    ~~~

在调用 plot_learning_curve 时，首先定义交叉验证 cv 和学习模型 estimator。

这里交叉验证用的是 ShuffleSplit，它首先将样例打散，并随机取 20％的数据作为测试集，这样取出 100 次，最后返回的是 train_index, test_index，就知道哪些数据是 train，哪些数据是 test。

estimator 用的是 GaussianNB，对应左图：

cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
estimator = GaussianNB()
plot_learning_curve(estimator, title, X, y, ylim=(0.7, 1.01), cv=cv, n_jobs=4)

再看 estimator 是 SVC 的时候，对应右图：

cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
estimator = SVC(gamma=0.001)
plot_learning_curve(estimator, title, X, y, (0.7, 1.01), cv=cv, n_jobs=4)

实例2

from sklearn.naive_bayes import GaussianNB import numpy as np from sklearn.learning_curve import learning_curve #c查看是否过拟合

def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None, n_jobs=1, train_sizes=np.linspace(.05, 1., 20), verbose=0, plot=True):
    """
    画出data在某模型上的learning curve.
    参数解释
    ----------
    estimator : 你用的分类器。
    title : 表格的标题。
    X : 输入的feature，numpy类型
    y : 输入的target vector
    ylim : tuple格式的(ymin, ymax), 设定图像中纵坐标的最低点和最高点
    cv : 做cross-validation的时候，数据分成的份数，其中一份作为cv集，其余n-1份作为training(默认为3份)
    n_jobs : 并行的的任务数(默认1)
    """
    train_sizes, train_scores, test_scores = learning_curve(
        estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes, verbose=verbose)

    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)

    if plot:
        plt.figure()
        plt.title(title)
        if ylim is not None:
            plt.ylim(*ylim)
        plt.xlabel(u"train_sample")
        plt.ylabel(u"score")
        plt.gca().invert_yaxis()
        plt.grid()

        plt.fill_between(train_sizes, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std,
                         alpha=0.1, color="b")
        plt.fill_between(train_sizes, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std,
                         alpha=0.1, color="r")
        plt.plot(train_sizes, train_scores_mean, 'o-', color="b", label=u"train_score")
        plt.plot(train_sizes, test_scores_mean, 'o-', color="r", label=u"cross_validation_score")

plt.legend(loc="best")

        plt.draw()
        plt.show()
        plt.gca().invert_yaxis()
        plt.savefig("learn_curve.jpg")

    midpoint = ((train_scores_mean[-1] + train_scores_std[-1]) + (test_scores_mean[-1] - test_scores_std[-1])) / 2
    diff = (train_scores_mean[-1] + train_scores_std[-1]) - (test_scores_mean[-1] - test_scores_std[-1])
    return midpoint, diff
if __name__=='__main__':
X=np.array([[ 1.        , -0.12493874, 0.04575749],
       [ 0.        , -0.30103   , 0.03140846],
       [ 1.        , -0.17609126, 0.11394335],
       [ 1.        , -0.30103   , -0.06694679],
       [ 1.        , -0.30103   , -0.12104369],
       [ 1.        , -0.23408321, 0.11270428],
       [ 1.        , 0.19188553, 0.22577904],
       [ 1.        , -0.23736092, -0.42100531],
       [ 0.        , 0.21085337, 0.13966199],
       [ 1.        , -0.06214791, 0.07716595],
       [ 1.        , 0.14612804, -0.01223446],
       [ 1.        , 0.1383027 , 0.1217336 ],
       [ 1.        , -0.30103   , -0.18073616],
       [ 0.        , 0.02996322, -0.09108047],
       [ 0.        , 0.05435766, 0.1638568 ],
       [ 1.        , -0.11394335, 0.        ],
       [ 1.        , 0.06694679, 0.30998484],
       [ 0.        , 0.64345268, 0.02802872],
       [ 1.        , 0.        , -0.01639042],
       [ 0.        , 0.11394335, -0.0234811 ],
       [ 0.        , 0.        , 0.18799048],
       [ 1.        , 0.        , 0.10914447],
       [ 1.        , -0.04139269, 0.        ],
       [ 0.        , 0.18905624, 0.17026172],
       [ 1.        , -0.14132915, 0.15209098],
       [ 0.        , 0.30103   , 0.27036118],
       [ 1.        , 0.22184875, 0.05435766],
       [ 0.        , 0.34242268, 0.09455611],
       [ 1.        , -0.20411998, -0.1173856 ],
       [ 0.        , 0.11394335, 0.01189922],
       [ 1.        , -0.22184875, -0.01378828],
       [ 1.        , 0.13262557, 0.14390658],
       [ 0.        , 0.14612804, 0.13353891]])

y=np.array([1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1,
0, 1, 0, 0, 0, 1, 0, 1, 0, 0])

Gmodel=GaussianNB()
train_sizes, train_scores, test_scores=learning_curve(Gmodel,X,y,train_sizes=[3,6,10],cv=3)
plot_learning_curve(Gmodel, u"learning curve", X, y)

数据结果

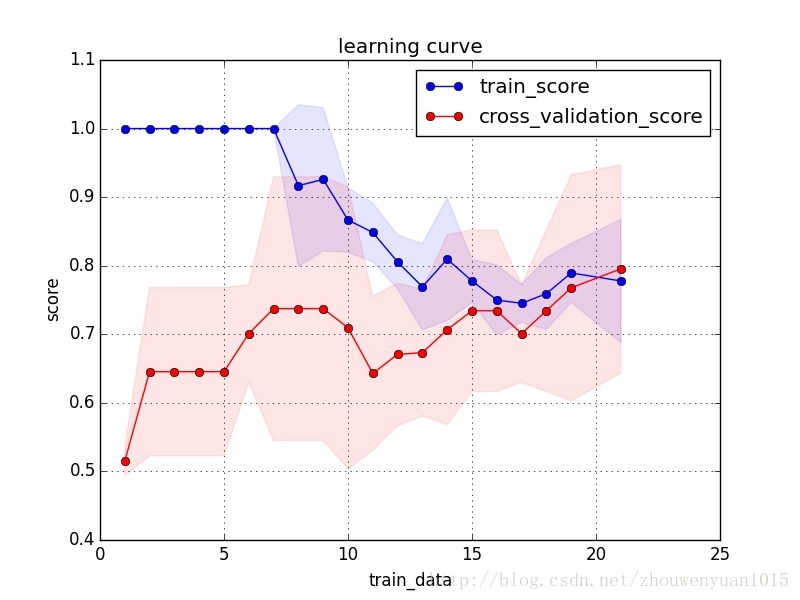
这里写图片描述

注：测试样本量较少，在样本量为10处存在一些过拟合

资料：
http://scikit-learn.org/stable/modules/learning_curve.html#learning-curve
http://scikit-learn.org/stable/auto_examples/model_selection/plot_learning_curve.html#sphx-glr-auto-examples-model-selection-plot-learning-curve-py

http://blog.csdn.net/han_xiaoyang/article/details/49797143

二、过拟合和欠拟合

2.1机器学习中解决欠拟合方法

2.2机器学习中解决过拟合方法

在进行数据挖掘或者机器学习模型建立的时候，因为在统计学习中，假设数据满足独立同分布，即当前已产生的数据可以对未来的数据进行推测与模拟，因此都是使用历史数据建立模型，即使用已经产生的数据去训练，然后使用该模型去拟合未来的数据。但是一般独立同分布的假设往往不成立，即数据的分布可能会发生变化（distribution drift），并且可能当前的数据量过少，不足以对整个数据集进行分布估计，因此往往需要防止模型过拟合，提高模型泛化能力。而为了达到该目的的最常见方法便是：正则化，即在对模型的目标函数（objective function）或代价函数（cost function）加上正则项。
在对模型进行训练时，有可能遇到训练数据不够，即训练数据无法对整个数据的分布进行估计的时候，或者在对模型进行过度训练（overtraining）时，常常会导致模型的过拟合（overfitting）。如下图所示：
这里写图片描述
通过上图可以看出，随着模型训练的进行，模型的复杂度会增加，此时模型在训练数据集上的训练误差会逐渐减小，但是在模型的复杂度达到一定程度时，模型在验证集上的误差反而随着模型的复杂度增加而增大。此时便发生了过拟合，即模型的复杂度升高，但是该模型在除训练集之外的数据集上却不work。

1. 参数范数惩罚(L1、L2正则化)

范数正则化是一种非常普遍的方法,也是最常用的方法,假如优化:

minObj(θ)=L(y,f(x))+αG(θ)minObj(θ)=L(y,f(x))+αG(θ)
其中LL为经验风险,其为在训练样本上的误差,而GG为对参数的惩罚,也叫结构风险.αα是平衡两者,如果太大则对应的惩罚越大,如过太小,甚至接近与0,则没有惩罚.
最常用的范数惩罚为L1,L2正则化。

以线性回归为例，L1又被成为Lasso: ||w||1=|w1|+|w2|+...||w||1=|w1|+|w2|+...，即绝对值相加,其趋向于是一些参数为0.可以起到特征选择的作用. L2正则化为: ||w||2=w12+w22+...−−−−−−−−−−−−√||w||2=w12+w22+...，其趋向与,使权重很小.其又成为ridge.

L1正则
L1正则是基于L1范数，即在目标函数后面加上参数的L1范数和项，即参数绝对值和与参数的积项，即：

其中C0C0代表原始的代价函数，nn是样本的个数，λλ就是正则项系数，权衡正则项与C0C0项的比重。后面那一项即为L1正则项。
在计算梯度时，ww的梯度变为：

其中，sgnsgn是符号函数，那么便使用下式对参数进行更新：

对于有些模型，如线性回归中（L1正则线性回归即为Lasso回归），常数项bb的更新方程不包括正则项，即：

其中，梯度下降算法中，α<0,β<0α<0,β<0，而在梯度上升算法中则相反。
从上式可以看出，当ww为正时，更新后ww会变小；当ww为负时，更新后ww会变大；因此L1正则项是为了使得那些原先处于零（即|w|≈0|w|≈0）附近的参数ww往零移动，使得部分参数为零，从而降低模型的复杂度（模型的复杂度由参数决定），从而防止过拟合，提高模型的泛化能力。
其中，L1正则中有个问题，便是L1范数在0处不可导，即|w||w|在0处不可导，因此在ww为0时，使用原来的未经正则化的更新方程来对ww进行更新，即令sgn(0)=0sgn(0)=0，这样即：

L2正则
L2正则是基于L2范数，即在目标函数后面加上参数的L2范数和项，即参数的平方和与参数的积项，即：

其中C0C0代表原始的代价函数，nn是样本的个数，与L1正则化项前面的参数不同的是，L2项的参数乘了1212，是为了便于计算以及公式的美感性，因为平方项求导有个2，λλ就是正则项系数，权衡正则项与C0C0项的比重。后面那一项即为L2正则项。
L2正则化中则使用下式对模型参数进行更新：

对于有些模型，如线性回归中（L2正则线性回归即为Ridge回归，岭回归），常数项bb的更新方程不包括正则项，即：

其中，梯度下降算法中，α<0,β<0α<0,β<0，而在梯度上升算法中则相反。
从上式可以看出，L2正则项起到使得参数ww变小加剧的效果，但是为什么可以防止过拟合呢？一个通俗的理解便是：更小的参数值ww意味着模型的复杂度更低，对训练数据的拟合刚刚好（奥卡姆剃刀），不会过分拟合训练数据，从而使得不会过拟合，以提高模型的泛化能力。
在这里需要提到的是，在对模型参数进行更新学习的时候，有两种更新方式，mini-batch （部分增量更新）与 full-batch（全增量更新），即在每一次更新学习的过程中（一次迭代，即一次epoch），在mini-batch中进行分批处理，先使用一部分样本进行更新，然后再使用一部分样本进行更新。直到所有样本都使用了，这次epoch的损失函数值则为所有mini batch的平均损失值。设每次mini batch中样本个数为mm，那么参数的更新方程中的正则项要改成：

而full-batch即每一次epoch中，使用全部的训练样本进行更新，那么每次的损失函数值即为全部样本的误差之和。更新方程不变。
总结
正则项是为了降低模型的复杂度，从而避免模型区过分拟合训练数据，包括噪声与异常点（outliers）。从另一个角度上来讲，正则化即是假设模型参数服从先验概率，即为模型参数添加先验，只是不同的正则化方式的先验分布是不一样的。这样就规定了参数的分布，使得模型的复杂度降低（试想一下，限定条件多了，是不是模型的复杂度降低了呢），这样模型对于噪声与异常点的抗干扰性的能力增强，从而提高模型的泛化能力。还有个解释便是，从贝叶斯学派来看：加了先验，在数据少的时候，先验知识可以防止过拟合；从频率学派来看：正则项限定了参数的取值，从而提高了模型的稳定性，而稳定性强的模型不会过拟合，即控制模型空间。
另外一个角度，过拟合从直观上理解便是，在对训练数据进行拟合时，需要照顾到每个点，从而使得拟合函数波动性非常大，即方差大。在某些小区间里，函数值的变化性很剧烈，意味着函数在某些小区间里的导数值的绝对值非常大，由于自变量的值在给定的训练数据集中的一定的，因此只有系数足够大，才能保证导数的绝对值足够大。如下图（引用知乎）：

另外一个解释，规则化项的引入，在训练（最小化cost）的过程中，当某一维的特征所对应的权重过大时，而此时模型的预测和真实数据之间距离很小，通过规则化项就可以使整体的cost取较大的值，从而，在训练的过程中避免了去选择那些某一维（或几维）特征的权重过大的情况，即过分依赖某一维（或几维）的特征（引用知乎）。
L2与L1的区别在于，L1正则是拉普拉斯先验，而L2正则则是高斯先验。它们都是服从均值为0，协方差为1λ1λ。当λ=0λ=0时，即没有先验）没有正则项，则相当于先验分布具有无穷大的协方差，那么这个先验约束则会非常弱，模型为了拟合所有的训练集数据，参数ww可以变得任意大从而使得模型不稳定，即方差大而偏差小。λλ越大，标明先验分布协方差越小，偏差越大，模型越稳定。即，加入正则项是在偏差bias与方差variance之间做平衡tradeoff（来自知乎）。下图即为L2与L1正则的区别：

上图中的模型是线性回归，有两个特征，要优化的参数分别是w1和w2，左图的正则化是L2，右图是L1。蓝色线就是优化过程中遇到的等高线，一圈代表一个目标函数值，圆心就是样本观测值（假设一个样本），半径就是误差值，受限条件就是红色边界（就是正则化那部分），二者相交处，才是最优参数。可见右边的最优参数只可能在坐标轴上，所以就会出现0权重参数，使得模型稀疏。
其实拉普拉斯分布与高斯分布是数学家从实验中误差服从什么分布研究中得来的。一般直观上的认识是服从应该服从均值为0的对称分布，并且误差大的频率低，误差小的频率高，因此拉普拉斯使用拉普拉斯分布对误差的分布进行拟合，如下图：

而拉普拉斯在最高点，即自变量为0处不可导，因为不便于计算，于是高斯在这基础上使用高斯分布对其进行拟合，如下图：

2. 数据增强

在数据挖掘领域流行着这样的一句话，“有时候往往拥有更多的数据胜过一个好的模型”。因为我们在使用训练数据训练模型，通过这个模型对将来的数据进行拟合，而在这之间又一个假设便是，训练数据与将来的数据是独立同分布的。即使用当前的训练数据来对将来的数据进行估计与模拟，而更多的数据往往估计与模拟地更准确。因此，更多的数据有时候更优秀。但是往往条件有限，如人力物力财力的不足，而不能收集到更多的数据，如在进行分类的任务中，需要对数据进行打标，并且很多情况下都是人工得进行打标，因此一旦需要打标的数据量过多，就会导致效率低下以及可能出错的情况。所以，往往在这时候，需要采取一些计算的方式与策略在已有的数据集上进行手脚，以得到更多的数据。
通俗得讲，数据机扩增即需要得到更多的符合要求的数据，即和已有的数据是独立同分布的，或者近似独立同分布的。一般有以下方法：

从数据源头采集更多数据
复制原有数据并加上随机噪声
重采样
根据当前数据集估计数据分布参数，使用该分布产生更多数据等

如图像处理：

图像平移。这种方法可以使得网络学习到平移不变的特征。
图像旋转。学习旋转不变的特征。有些任务里，目标可能有多种不同的姿态，旋转正好可以弥补样本中姿态较少的问题。
图像镜像。和旋转的功能类似。
图像亮度变化。甚至可以用直方图均衡化。
裁剪。
缩放。
图像模糊。用不同的模板卷积产生模糊图像。

3. 提前终止

如下图所示(图片来源deep learning),当随着模型的能力提升,训练集的误差会先减小再增大,这样可以提前终止算法减缓过拟合现象.

这里写图片描述

对模型进行训练的过程即是对模型的参数进行学习更新的过程，这个参数学习的过程往往会用到一些迭代方法，如梯度下降（Gradient descent）学习算法。Early stopping便是一种迭代次数截断的方法来防止过拟合的方法，即在模型对训练数据集迭代收敛之前停止迭代来防止过拟合。
Early stopping方法的具体做法是，在每一个Epoch结束时（一个Epoch集为对所有的训练数据的一轮遍历）计算validation data的accuracy，当accuracy不再提高时，就停止训练。这种做法很符合直观感受，因为accurary都不再提高了，在继续训练也是无益的，只会提高训练的时间。那么该做法的一个重点便是怎样才认为validation accurary不再提高了呢？并不是说validation accuracy一降下来便认为不再提高了，因为可能经过这个Epoch后，accuracy降低了，但是随后的Epoch又让accuracy又上去了，所以不能根据一两次的连续降低就判断不再提高。一般的做法是，在训练的过程中，记录到目前为止最好的validation accuracy，当连续10次Epoch（或者更多次）没达到最佳accuracy时，则可以认为accuracy不再提高了。此时便可以停止迭代了（Early Stopping）。这种策略也称为“No-improvement-in-n”，n即Epoch的次数，可以根据实际情况取，如10、20、30……

提前终止是一种很常用的缓解过拟合的方法,如在决策树的先剪枝的算法,提前终止算法,使得树的深度降低,防止其过拟合.

4. 参数绑定与参数共享

在卷积神经网络CNN中(计算机视觉与卷积神经网络 ),卷积层就是其中权值共享的方式,一个卷积核通过在图像上滑动从而实现共享参数,大幅度减少参数的个数,用卷积的形式是合理的,因为对于一副猫的图片来说,右移一个像素同样还是猫,其具有局部的特征.这是一种很好的缓解过拟合现象的方法.
同样在RNN中用到的参数共享,在其整条时间链上可以进行参数的共享,这样才使得其能够被训练.

5. bagging 和其他集成方法

其实bagging的方法是可以起到正则化的作用,因为正则化就是要减少泛化误差,而bagging的方法可以组合多个模型起到减少泛化误差的作用.
在深度学习中同样可以使用此方法,但是其会增加计算和存储的成本.

6. Dropout

Dropout提供了一种廉价的Bagging集成近似,能够训练和评估指数级数量的神经网络。dropout可以随机的让一部分神经元失活,这样仿佛是bagging的采样过程,因此可以看做是bagging的廉价的实现.
但是它们训练不太一样,因为bagging,所有的模型都是独立的,而dropout下所有模型的参数是共享的.
通常可以这样理解dropout:假设我们要判别一只猫,有一个神经元说看到有毛就是猫,但是如果我让这个神经元失活,它还能判断出来是猫的话,这样就比较具有泛化的能力,减轻了过拟合的风险.

正则是通过在代价函数后面加上正则项来防止模型过拟合的。而在神经网络中，有一种方法是通过修改神经网络本身结构来实现的，其名为Dropout。该方法是在对网络进行训练时用一种技巧（trick），对于如下所示的三层人工神经网络：

对于上图所示的网络，在训练开始时，随机得删除一些（可以设定为一半，也可以为1/3，1/4等）隐藏层神经元，即认为这些神经元不存在，同时保持输入层与输出层神经元的个数不变，这样便得到如下的ANN：

然后按照BP学习算法对ANN中的参数进行学习更新（虚线连接的单元不更新，因为认为这些神经元被临时删除了）。这样一次迭代更新便完成了。下一次迭代中，同样随机删除一些神经元，与上次不一样，做随机选择。这样一直进行瑕疵，直至训练结束。
Dropout方法是通过修改ANN中隐藏层的神经元个数来防止ANN的过拟合。

7. 辅助分类节点(auxiliary classifiers)

在Google Inception V1中,采用了辅助分类节点的策略,即将中间某一层的输出用作分类,并按一个较小的权重加到最终的分类结果中,这样相当于做了模型的融合,同时给网络增加了反向传播的梯度信号,提供了额外的正则化的思想.

8. Batch Normalization

在Google Inception V2中所采用,是一种非常有用的正则化方法,可以让大型的卷积网络训练速度加快很多倍,同事收敛后分类的准确率也可以大幅度的提高.
BN在训练某层时,会对每一个mini-batch数据进行标准化(normalization)处理,使输出规范到N(0,1)的正太分布,减少了Internal convariate shift(内部神经元分布的改变),传统的深度神经网络在训练是,每一层的输入的分布都在改变,因此训练困难,只能选择用一个很小的学习速率,但是每一层用了BN后,可以有效的解决这个问题,学习速率可以增大很多倍.

未完待续…