目录



关于L2使W变小,但是不为0的第二中解释。对于L2,最优解是导数等于0处。另导数等于0,得出W= L' /2 *lamda. 因为L'不等于0.所以W不会等于0.
关于L1使W趋向于0: 因为W不等于0的时候,L'是线段的端点,而W等于0的时候是一个线段。明显占的比重更大,W更大概率向0约束。
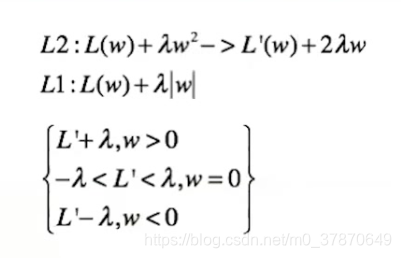
L1正则化使得模型更加稀疏,L2使得模型参数更趋近于0,提高泛化能力(这里是另外一个解释:https://www.zhihu.com/question/38081976/answer/74895039
机器学习中的范数规则化之(一)L0、L1与L2范数:https://blog.csdn.net/zouxy09/article/details/24971995?ADUIN=189151916&ADSESSION=1451702742&ADTAG=CLIENT.QQ.5449_.0&ADPUBNO=26525)
先介绍下各自的用处:

L0范数
就是指矩阵中非零元素的个数,很显然,在损失函数后面加上L0正则项就能够得到稀疏解,但是L0范数很难求解,是一个NP问题,因此转为求解相对容易的L1范数(l1能够实现稀疏性是因为l1是L0范数的最优凸近似) 
L1范数
矩阵中所有元素的绝对值的和。损失函数后面加上L1正则项就成了著名的Lasso问题(Least Absolute Shrinkage and Selection Operator),L1范数可以约束方程的稀疏性,该稀疏性可应用于特征选择:
比如,有一个分类问题,其中一个类别Yi(i=0,1),特征向量为Xj(j=0,1~~~1000),那么构造一个方程
Yi = W0*X0+W1*X1···Wj*Xj···W1000*X1000+b;
其中W为权重系数,那么通过L1范数约束求解,得到的W系数是稀疏的,那么对应的X值可能就是比较重要的,这样就达到了特征选择的目的(该例子是自己思考后得出的,不知道正不正确,欢迎指正)。
L2范数
其实就是矩阵所有元素的平方和开根号,即欧式距离,在回归问题中,在损失函数(或代价函数)后面加上L2正则项就变成了岭回归(Ridge Regression),也有人叫他权重衰减,L2正则项的一个很大的用处就是用于防止机器学习中的过拟合问题,同L1范数一样,L2范数也可以对方程的解进行约束,但他的约束相对L1更平滑,在模型预测中,L2往往比L1好。L2会让W的每个元素都很小,接近于0,但是不会等于0.而越小的参数模型越简单,越不容易产生过拟合,以下引自另一篇文章:
到目前为止,我们只是解释了L2正则化项有让w“变小”的效果(公式中的lamda越大,最后求得的w越小),但是还没解释为什么w“变小”可以防止overfitting?一个所谓“显而易见”的解释就是:更小的权值w,从某种意义上说,表示网络的复杂度更低,对数据的拟合刚刚好(这个法则也叫做奥卡姆剃刀),而在实际应用中,也验证了这一点,L2正则化的效果往往好于未经正则化的效果。当然,对于很多人(包括我)来说,这个解释似乎不那么显而易见,所以这里添加一个稍微数学一点的解释:
过拟合的时候,拟合函数的系数往往非常大,为什么?如下图所示,过拟合,就是拟合函数需要顾忌每一个点,最终形成的拟合函数波动很大。在某些很小的区间里,函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值(绝对值)非常大,由于自变量值可大可小,所以只有系数足够大,才能保证导数值很大。 
而正则化是通过约束参数的范数使其不要太大,所以可以在一定程度上减少过拟合情况。
弹性网络(Elastic Net):实际上是L1,L2的综合
其中的L1正则项产生稀疏模型
L2正则项产生以下几个作用:
1 消除L1正则项中选择变量个数的限制(即稀疏性)
2 产生grouping effect(对于一组相关性较强的原子,L1会在相关的变量间***随机***的选择一个来实现稀疏)
3 稳定L1正则项的路径
整理后的正则项:
elastic net 的几何结构:
其结构有如下两个特点:
1 在顶点具有奇异性(稀疏性的必要条件)
2 严格的凸边缘(凸效应的强度随着α而变化(产生grouping效应))
elastic net总结:
1 弹性网络同时进行正则化与变量选择
2 能够进行grouped selection
3 当p>>n,或者严重的多重共线性情况时,效果明显
4 当α接近0时,elastic net表现接近lasso,但去掉了由极端相关引起的退化或者奇怪的表现
5 当α从1变化到0时,目标函数的稀疏解(系数为0的情况)从0增加到lasso的稀疏解L1 和L2区别总结:
加入正则项是为了避免过拟合,或解进行某种约束,需要解保持某种特性
L1正则假设参数的先验分布是Laplace分布,可以保证模型的稀疏性,也就是某些参数等于0,L1正则化是L0正则化的最优凸近似,比L0容易求解,并且也可以实现稀疏的效果,
L1也称Lasso;
L2正则假设参数的先验分布是Gaussian分布,可以保证模型的稳定性,也就是参数的值不会太大或太小.L2范数是各参数的平方和再求平方根,我们让L2范数的正则项最小,可以使W的每个元素都很小,都接近于0。但与L1范数不一样的是,它不会是每个元素为0,而只是接近于0。越小的参数说明模型越简单,越简单的模型越不容易产生过拟合现象。
L2正则化江湖人称Ridge,也称“岭回归”
在实际使用中,如果特征是高维稀疏的,则使用L1正则;如果特征是低维稠密的,则使用L2正则。
L2不能控制feature的“个数”,但是能防止模型overfit到某个feature上;相反L1是控制feature“个数”的,并且鼓励模型在少量几个feature上有较大的权重。
数学公式解释
- L1的权值更新公式为
wi = wi – η * 1, 权值每次更新都固定减少一个特定的值(学习速率),那么经过若干次迭代之后,权值就有可能减少到0。 - L2的权值更新公式为
wi = wi – η * wi,虽然权值不断变小,但每次减小的幅度不断降低,所以很快会收敛到较小的值但不为0。
几何空间解释

在二维空间中,左边的方形线上是L1中w1/w2取值区间,右边得圆形线上是L2中w1/w2的取值区间,圆圈表示w1/w2取不同值时整个正则化项的值的等高线。从等高线和w1/w2取值区间的交点可以看到,L1中两个权值倾向于一个较大另一个为0,L2中两个权值倾向于均为非零的较小数。
实际使用过程中,如果数据量不是很大,用L2的精度要好。
多重共线性(multicollinearity)指的是你建模的时候,解释变量之间有高度相关性。

1.https://www.jianshu.com/p/4bad38fe07e6
2.https://blog.csdn.net/jinping_shi/article/details/52433975
3.https://blog.csdn.net/ningyanggege/article/details/81133785
从偏差和方差角度理解正则
运用不同的λ去最小化“代价函数”得到不同的Θ;
不同的Θ带入h(x)中得到不同的模型,然后用“交叉验证集”验证;
取“交叉验证误差”最小的那个模型;
将最终得到的模型运用于测试集,测试模型的表现。
下图为不同λ下“训练误差”和“交叉验证误差”的变化
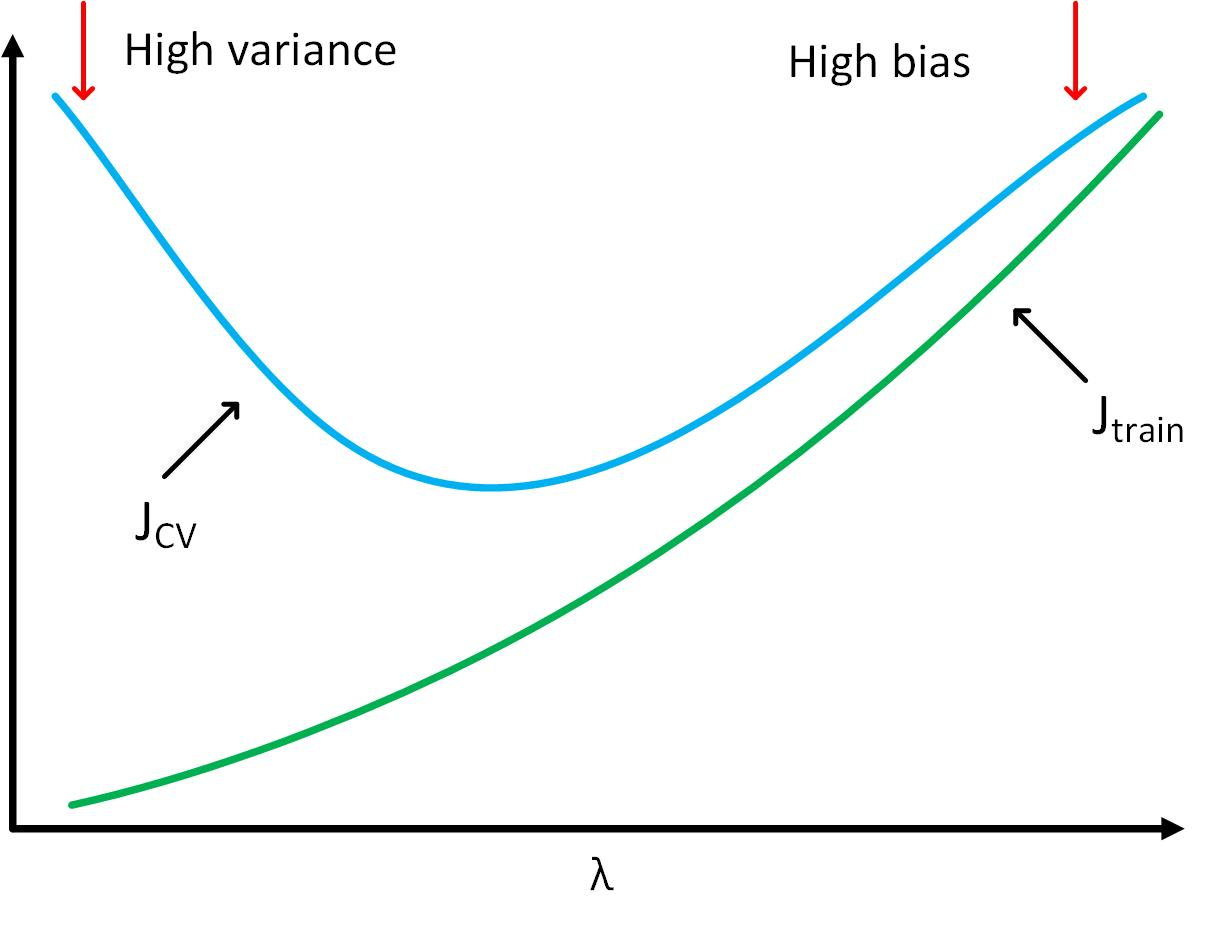 可以得到
可以得到
- 当λ很小时,模型处于“高方差”状态,“训练误差”很小,“交叉验证误差”较大
- 当λ很大时,模型处于“高偏差”状态,“训练误差”和“交叉验证误差”都很大
相关参考:
https://blog.csdn.net/LIYUAN123ZHOUHUI/article/details/51882926


























 690
690

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








