论文题目
A Bayesian approach to single-particle electron cryo-tomography in RELION-4.0
作者:Jasenko Zivanov(一作,MRC实验室)
回顾
RELION-3 为subtomo 新引入了 3D CTF 和 missing-wedge model。

Problems:
- no sound statistical assumptions can be made about tomogram voxels(对于断层扫描体素,我们无法做出可靠的统计假设)。
- 数据是 2D pixels, 不是3D voxels。
- tomogram reconstruction 的影响被忽略。
- tomograms 数据量很大(~60GB)。
Idea:pseudo-subtomograms
- Place the meatured 2D images in a hypothetical 3D space. 将经过处理的2D图像放置在一个假设的3D空间中。
- Contruct acstract 3D images (pseudo-subtomograms) for each particle. 为每个粒子构造一个三维图像(伪亚层析图)。
- Pseudo-subtomos are not approximations of a 3D density. 伪亚层析图不是三维密度的近似。
- Pseudo-subtomos trick RELION into approximating the likelihood that would arise from working on 2D images. 使其近似于处理2D图像所产生的可能性。
Advantages:
- Approximates a plausible statistical model on the 2D raw images. 在二维原始图像上近似一个可靠的统计模型。
- Use existing methods in RELION for refinement, classification, symmetry expansion, multi-body, … 使用RELION 现有的方法
- 3D average map reconstructed straight from all the relevant areas in the 2D images. 直接从 2D 图像中的所有相关区域重建 3D 平均 map
- 3D reference allows tilt-series parameters to be optimised, leading to iteratively improved 3D maps and pseudo-subtomograms. 3D 参考允许倾斜系列参数优化,导致迭代改进 3D map 和伪亚层析图。
New features:
- Subtomograms averaging(Joaquin & Jasenko)
- Pseudo-subtomograms
- CTF refinement,Bayesian polishing
摘要
本文提出了一种从冷冻断层扫描数据集中的多个颗粒确定大分子结构的新方法。虽然现有的子断层平均方法是基于三维数据模型的,但是本文建议优化一个近似于二维实验图像的函数的正则化似然目标。
此外,类似于单颗粒分析中的贝叶斯抛光和CTF细化,本文利用信噪比得到增强的平均结构去优化倾斜序列的对齐、颗粒的电子束诱导运动、每个颗粒的散焦、以及显微镜的高阶光学相差。
方法都在RELION-4.0中实现,对熟悉单颗粒分析流程的研究人员很友好。
本文举了两个例子证明了该方法可以利用cryo-ET数据从头获得原子级别的大分子结构重建。
Introduction
背景介绍
近年来,冷冻电镜(cryo-EM)已经允许对越来越多的生物大分子进行三维成像,其分辨率足以进行从头原子建模。这种发展最初是由检测器技术的进步推动的,而新的、稳健的图像处理算法进一步促进了这种发展。
介绍单颗粒分析技术
如今,很多单颗粒分析的工作流程只需要极少的人力监督就可以完成。例如图像中颗粒的检测提取和初始分类、三维重建、以及光学参数的细化和每个颗粒在电子束诱导下的运动轨迹。构成这些现代方法的许多算法都建立在坚实的统计基础上,只需要很少的可调参数。这减少了对操作人员专业知识的需要,并提供了客观性,以及鲁棒性,以获得最佳结构。
引出 cryoET 和 subtomo
然而,单颗粒方法仅限于研究分离的蛋白质复合物,这些复合物被纯化到相对均匀。为了在生物学背景下研究这些复合物,可以使用电子低温断层扫描(cryo-ET)代替。在层析方法中,图像采集过程中样本被倾斜多次,产生所谓的倾斜序列图像,从中可以计算出三维层析图。与单粒子分析的方式相同,在那些层析图中重复出现的粒子,可以进行对齐和平均以获得更高分辨率的重建,这个过程被称为子断层平均 (subtomogram averaging)。
与单颗粒分析领域不同,许多用于子断层图平均的工具仍然需要较高的专业知识水平,通常是为了调整来自底层算法中的启发式参数。这不仅阻碍了新科学家进入该领域,还可能导致计算出的结构不是最优的。
subtomo 面对的挑战
subtomo 和单颗粒分析相比还面对一些特有的挑战:
除了要估计每个颗粒的位置和方向,算法还要考虑到倾斜序列的几何特征。通常,这是通过一组预处理步骤来解决的,这些步骤包括:对比度传递函数(CTF)参数估计和倾斜序列对齐,然后重建整个视场的层析图像(通常大得不方便)。然后从层析图中提取选定颗粒周围的较小的子层析图,并用于子层析图对齐和平均的单独过程。层析图的重建过程和子层析图平均过程的分离可能会导致误差的累积,因为CTF估计或倾斜序列校准中的误差很难纠正。此外,子层析图的平均还会受到缺失楔的影响(由于样品不能在显微镜内旋转180度,亚层析图像在傅里叶空间中含有空白区域),这在亚层析图像平均中是很难处理的。
介绍以前的subtomo averaging算法
亚层析图平均的一个基本问题是将原始二维图像数据转换为三维 subtomogram,然后用三维亚层析图代替实验数据进行对齐算法。RELION-3 引入了三维CTF的概念来描述从二维图像到 subtomogram 的信息传递,通过重建算法中的插值处理,在一定程度上解决了楔形缺失和信息丢失的问题。3D CTF 方法的一个缺点是它不能正确处理傅里叶空间的低分辨率区域,这些区域中来自不同倾斜图像的信息会发生重叠。
引出本文的新算法
一种统计上更吸引人的方法是将最优化目标函数直接表示为在显微镜中测量的实际2D图像的函数。这是在一种称为约束单颗粒 cryo-ET 的方法中提出的。在这种方法中,从倾斜系列图像中单独框出来的颗粒像在单颗粒分析中一样被处理,但它们的相对方向保持固定。为了处理倾斜系列图像中粒子相对方向的未知,以及它们的CTF, M 程序最近引入了新的优化方法,将参考投影与2D粒子图像进行比较。M仍然依赖于RELION-3来对齐和分类3D亚层析图,这些亚层析图是根据M中的优化参数重新计算出来的。然而,这种迭代方法允许 subtomo averaging 得到接近于SPA中观察到的分辨率,甚至是对于复杂细胞环境中的粒子。
简介本文算法
本文描述了 RELION-4.0 中的一种新方法,它将 subtomogram averaging 作为直接依赖于2D倾斜序列图像的正则似然函数的优化。为了让计算量和实现成本可接受,我们将主要的 refinement 程序实现为 pseudo subtomograms:明确构造的 3D 数据数组集,其中包含预乘了CTF的倾斜系列图像的总和,以及包含相应 CTF 平方和的辅助数组 以及 每个 3D 体素被观察到的频率。
pseudo subtomograms 不再旨在代表底层粒子的实际散射潜力。 相反,它们代表了一种在现有 RELION 代码中实现 2D 方法的便捷方式。 在给定当前模型的情况下,RELION-4.0 对子断层图的评估近似于在整个倾斜系列的图像中观察到假设粒子的可能性。 使用该可能性作为度量,现在可以对断层数据执行与单颗粒分析中等效的操作,例如 3D 初始模型生成、3D 分类或高分辨率细化。
此外,我们描述了利用平均结构中增加的信噪比优化倾斜系列参数的新方法。 除了优化倾斜系列对齐本身之外,我们还描述了类似于 CTF 细化的方法,用于细化光学特性(散焦、散光和高阶像差)的描述符,以及类似于贝叶斯抛光的方法,在整个倾斜系列中模拟电子束诱导的颗粒运动。 一旦优化了所有这些参数,就可以构建新的伪子断层图并重复对齐步骤。 迭代的图像处理工作流程类似于 RELION 中现有的单颗粒分析方法。
方法
Particle alignment and averaging
RELION 执行最大后验估计,以找到一组模型参数
Θ
\Theta
Θ,其使观察实验图像
X
\mathbb{X}
X 的概率最大化。使用贝叶斯定理,我们将正则化似然优化目标函数定义为:
P
(
Θ
∣
X
)
=
P
(
X
∣
Θ
)
P
(
Θ
)
P(\Theta \mid \mathbb{X})=P(\mathbb{X} \mid \Theta) P(\Theta)
P(Θ∣X)=P(X∣Θ)P(Θ)
其中
P
(
Θ
)
P(Θ)
P(Θ) 表示关于模型的先验信息,即重建的密度图在傅里叶空间中的功率是被限制的,而
P
(
X
∣
Θ
)
P(\mathbb{X}|Θ)
P(X∣Θ) 是在给定模型的情况下观察到数据的可能性。 使用边缘化似然函数,对每个单独粒子的未知对齐
ϕ
\phi
ϕ 进行积分。 为简单起见,本文中使用的符号省略了这些积分。
这个数据模型假设单个粒子 p 的低温 EM 图像的傅立叶分量上存在独立的高斯噪声。 因此,我们把在假设的对齐 ϕ \phi ϕ 中观察到颗粒的负对数似然写为二维傅里叶像素 j ∈ R 2 j ∈ R^2 j∈R2 网格上的总和 (Eq 2):
−
log
(
P
(
X
∣
ϕ
)
)
∝
∑
j
∣
X
j
−
CTF
(
j
)
V
j
(
p
)
∣
2
σ
j
2
-\log (P(X \mid \phi)) \propto \sum_{\mathbf{j}} \frac{\left|X_{\mathbf{j}}-\operatorname{CTF}(\mathbf{j}) V_{\mathbf{j}}^{(p)}\right|^{2}}{\sigma_{j}^{2}}
−log(P(X∣ϕ))∝j∑σj2∣∣∣Xj−CTF(j)Vj(p)∣∣∣2
其中,
X
X
X 是图像的傅里叶变换,CTF 是衬度传递函数,
V
j
V_{\mathbf{j}}
Vj 表示从已知映射
V
V
V 的 3D傅里叶变换到粒子视图的 2D 切片,
σ
j
2
{\sigma_{j}^{2}}
σj2 是频带的噪声方差。
V
j
(
p
)
V_{\mathbf{j}}^{(p)}
Vj(p) 由下式得到 (Eq 3):
V
j
(
p
)
=
exp
(
i
t
p
⋅
j
)
V
(
A
p
j
)
V_{\mathbf{j}}^{(p)}=\exp \left(i \mathbf{t}_{p} \cdot \mathbf{j}\right) V\left(A_{p} \mathbf{j}\right)
Vj(p)=exp(itp⋅j)V(Apj)
其中,二维向量
t
p
\mathbf{t}_p
tp 和一个 2x3 的矩阵
A
p
A_p
Ap 分别封装了颗粒的位置和方向,然后
V
(
A
p
j
)
V(A_p\mathbf{j})
V(Apj) 通过线性插值来评估。
在扫描断层中,我们的目标是在倾斜序列上去近似相同的似然性。直接的等效是倾斜序列中所有图像
f
f
f 的相关区域的像素的总和 (Eq 4):
−
log
(
P
(
X
∣
ϕ
)
)
∝
∑
f
,
j
∣
X
f
j
−
C
T
F
f
(
j
)
V
f
j
(
p
)
∣
2
σ
j
2
-\log (P(X \mid \phi)) \propto \sum_{f, \mathbf{j}} \frac{\left|X_{f \mathbf{j}}-\mathrm{CTF}_{f}(\mathbf{j}) V_{f \mathbf{j}}^{(p)}\right|^{2}}{\sigma_{j}^{2}}
−log(P(X∣ϕ))∝f,j∑σj2∣∣∣Xfj−CTFf(j)Vfj(p)∣∣∣2
我们将移位和旋转建模为每粒子和每图像分量的组合 (Eq 5,6):
t
p
f
=
A
f
⊤
T
p
f
+
t
f
A
p
f
=
R
p
A
f
\begin{aligned} \mathbf{t}_{p f} &=A_{f}^{\top} \mathbf{T}_{p f}+\mathbf{t}_{f} \\ A_{p f} &=R_{p} A_{f} \end{aligned}
tpfApf=Af⊤Tpf+tf=RpAf
这里,保持每个粒子的旋转分量
R
p
R_p
Rp 在倾斜序列中的所有图像中都相同,只改变倾斜序列图像的旋转对齐
A
f
A_f
Af。反过来,倾斜序列对齐
A
f
A_f
Af 是在一个给定倾斜图像中的所有粒子共享的。
平移的逐个颗粒部分被建模为一个三维矢量 T p f ∈ R 3 T_{pf} ∈ R^3 Tpf∈R3,它可以在不同的倾斜图像 f f f 上变化。
这与单颗粒分析相反,在单颗粒分析中,电子束诱导的粒子运动可以作为预处理步骤进行校正,因此每个颗粒都与运动校正过的图像中的单个2D平移相关联。
对于我们的 pseudo-subtomogram 方法,我们现在通过对伪子层析图中的3D 体素
k
k
k 求和,来近似对 2D像素
j
j
j 和倾斜图像
f
f
f 的求和 (Eq 7):
−
log
(
P
(
X
∣
ϕ
)
)
∝
∑
k
∣
D
k
−
W
k
V
(
R
p
k
)
∣
2
M
k
σ
k
2
-\log (P(X \mid \phi)) \propto \sum_{\mathbf{k}} \frac{\left|D_{\mathbf{k}}-W_{\mathbf{k}} V\left(R_{p} \mathbf{k}\right)\right|^{2}}{M_{\mathbf{k}} \sigma_{\mathbf{k}}^{2}}
−log(P(X∣ϕ))∝k∑Mkσk2∣Dk−WkV(Rpk)∣2
这里,数据项
D
D
D,它的权值
W
W
W,和多重体积
M
M
M 是傅里叶域中的三维数组。它们一起构成了 pseudo subtomogram 。它们的构造如 Eq(8-10)。
D
k
=
∑
f
,
j
l
(
A
p
f
j
−
k
)
C
T
F
f
(
j
)
X
f
j
W
k
=
∑
f
,
j
l
(
A
p
f
j
−
k
)
∣
CTF
f
(
j
)
∣
2
M
k
=
∑
f
,
j
l
(
A
p
f
j
−
k
)
,
\begin{aligned} D_{\mathbf{k}} &=\sum_{f, \mathbf{j}} l\left(A_{p f} \mathbf{j}-\mathbf{k}\right) \mathrm{CTF}_{f}(\mathbf{j}) X_{f \mathbf{j}} \\ W_{\mathbf{k}} &=\sum_{f, \mathbf{j}} l\left(A_{p f} \mathbf{j}-\mathbf{k}\right)\left|\operatorname{CTF}_{f}(\mathbf{j})\right|^{2} \\ M_{\mathbf{k}} &=\sum_{f, \mathbf{j}} l\left(A_{p f} \mathbf{j}-\mathbf{k}\right), \end{aligned}
DkWkMk=f,j∑l(Apfj−k)CTFf(j)Xfj=f,j∑l(Apfj−k)∣CTFf(j)∣2=f,j∑l(Apfj−k),
这里
l
(
⋅
)
l(\cdot)
l(⋅) 表示带有前向映射的线性插值,即每个二维傅里叶像素
j
j
j 被投影到三维傅里叶空间,更新8个最近的体素。这使得二维图像在傅里叶空间中比在三维空间中更精细地采样,相当于在真实空间中更大的二维图像。这是理想的,因为高频信息通过CTF的作用在二维图像中扩散开来。
在方程8中,当二维图像被CTF再次调制后,信号的一半被重新定位,因此它适合于一个更小的实空间区域,这相当于一个不太精细采样的傅里叶体积。需要注意的是,只有一半的信号可以通过这种方式恢复——另一半信号被移动两倍,只能通过一个非常大的包围盒来恢复,即使在单粒子分析中,这也是不切实际的。
忽略将图像预乘了它们的CTF的区别,公式7 旨在等价于公式4。由于总方差定律 ⟨ ∣ X ∣ − C 2 ⟩ = ⟨ ∣ X − C ∣ 2 ⟩ − Var ( X ) \left\langle|\mathbf{X}|-\mathbf{C}^{2}\right\rangle=\left\langle|\mathbf{X}-\mathbf{C}|^{2}\right\rangle-\operatorname{Var}(\mathbf{X}) ⟨∣X∣−C2⟩=⟨∣X−C∣2⟩−Var(X),可以用多个分量的和来替换单个傅立叶分量 X f j X_f\mathbf{j} Xfj,其中 C C C 是一个常数, V a r ( ⋅ ) Var(\cdot) Var(⋅) 对于任何的对齐 R p R_p Rp 是保持不变的,所以可以被忽略。
方差 σ k 2 \sigma_{k}^{2} σk2 等效于 σ j 2 \sigma_{j}^{2} σj2,即 2D 图像中各个傅里叶分量中噪声的功率。 方程(7)的分母中的附加项 M k M_k Mk 源于观察到 M k M_k Mk 个独立随机变量之和的方差(每个变量的方差为 σ k 2 \sigma_k^2 σk2)等于 M k σ k 2 M_k\sigma_k^2 Mkσk2。
通过期望最大化来优化 Eq(1),同时使用 Eq(7) 构造似然函数,得到以下的 V V V 和 σ 2 \sigma^2 σ2 更新公式 (Eq 11-12):
V
k
=
∑
p
D
(
R
p
⊤
k
)
/
σ
k
2
∑
p
W
(
R
p
⊤
k
)
/
σ
k
2
+
1
/
τ
k
2
σ
k
2
=
1
N
k
∑
k
∈
S
k
1
M
k
∣
D
k
−
W
k
V
(
R
p
k
)
∣
2
,
\begin{aligned} V_{\mathbf{k}} &=\frac{\sum_{p} D\left(R_{p}^{\top} \mathbf{k}\right) / \sigma_{k}^{2}}{\sum_{p} W\left(R_{p}^{\top} \mathbf{k}\right) / \sigma_{k}^{2}+1 / \tau_{k}^{2}} \\ \sigma_{k}^{2} &=\frac{1}{N_{k}} \sum_{\mathbf{k} \in S_{k}} \frac{1}{M_{\mathbf{k}}}\left|D_{\mathbf{k}}-W_{k} V\left(R_{p} \mathbf{k}\right)\right|^{2}, \end{aligned}
Vkσk2=∑pW(Rp⊤k)/σk2+1/τk2∑pD(Rp⊤k)/σk2=Nk1k∈Sk∑Mk1∣Dk−WkV(Rpk)∣2,
其中
τ
k
2
\tau_{k}^{2}
τk2 来自先验
P
(
Θ
)
P(\Theta)
P(Θ),表示预期的、频率相关的信号功率;
τ
k
2
\tau_{k}^{2}
τk2 和
σ
k
2
\sigma_{k}^{2}
σk2 是通过对
τ
k
2
\tau_{\mathbf{k}}^{2}
τk2 和
σ
k
2
\sigma_{\mathbf{k}}^{2}
σk2 分别进行平均来计算的。 在由
S
k
S_k
Sk 描述的半径为
k
k
k 且厚度为 1 的空心球中,
N
k
N_k
Nk 是
S
k
S_k
Sk 中
M
k
>
0
M_k > 0
Mk>0 的体素总数,并且等式 (11)中
τ
k
2
\tau_{\mathbf{k}}^{2}
τk2 和
σ
k
2
\sigma_{\mathbf{k}}^{2}
σk2 的划分是逐元素评估的。
Orientational priors 旋转先验
对齐伪子断层图像的方法的一个优点是伪子断层图像本身的坐标系可以任意选择。 默认情况下,伪子断层图的创建方向与断层图相同,但用户可以选择以更有意义的方式对齐它们。 这是很有用的,因为许多蛋白质在断层照片内部以二维阵列的形式组织,例如在膜内部或作为衣壳样结构的一部分。 通常,这些阵列中的单个蛋白质分子相对于阵列的表面法线表现出有限的旋转自由度,尽管它们可能能够围绕该法线自由旋转。通过重建 Z 轴平行于 2D 阵列法线的伪子断层图像,使用倾斜角的旋转先验将限制阵列内粒子的摇摆量。 这不仅加速了细化,因为需要评估的方向更少,而且还可以解决更具挑战性的结构,因为允许的解决方案更少。
Tilt series refinement
对多个颗粒进行平均后,会让估计的密度图 V 中的信噪比增加。然后利用 V重新估计描述倾斜系列的参数。 这些程序不需要伪子断层图,而是通过将密度图的投影直接与从倾斜系列图像中提取的 2D 框的(傅立叶)像素进行比较来执行的,具有足够的大小来保存 CTF 离域信号。 然后通过最小化方程4中定义的负对数似然来估计各种倾斜系列参数,即预测和观察之间的噪声加权平方差之和。
要细化的倾斜序列特性可以分为两大类:光学和几何。光学细化涉及到CTF的不同参数,而几何细化旨在优化倾斜序列的对齐,以及单个粒子的电子束诱导运动。这两组算法都与RELION中对应的单颗粒算法密切相关,分别是光学像差细化[27,29]和贝叶斯抛光[28]。尽管算法之间有相似之处,但优化后的模型与单颗粒分析有很大的不同。附录中给出了光学和几何优化算法的实现细节。
RELION-4.0 中对断层扫描数据的 CTF 改进包括:对模拟频率相关辐射损伤、散焦、散光以及高阶对称和反对称像差的比例因子进行优化。
尽管视场内的单个粒子在倾斜序列图像中处于不同的离焦处,但它们的相对离焦是从倾斜序列的几何形状和断层图中粒子的已知 3D 位置已知的。 因此,可以同时考虑倾斜序列图像中的所有粒子,从而一次性有效地执行散焦估计。 为了做到这一点,我们修改了为单颗粒分析中的高阶像差估计而开发的程序 [29],其中来自每个倾斜序列图像中所有颗粒的信息被压缩成两个图像,用于估计一个常见的相移(见附录)。
类似的程序也可用于对断层扫描数据中的高阶对称和反对称像差进行建模。 类似于我们的单颗粒方法,它们使用 Zernike 多项式建模并以相同的方式进行估计。 由于高阶像差通常只是相对较高空间频率的限制因素,因此需要大量粒子才能可靠地估计它们。最佳情况下,将因此在整个数据集上全局估计高阶像差,并且仅适用于产生高分辨率平均值的情况。 只有在采集过程中变化太快的像差才需要将断层照片分成光学组并估计每个光学组的像差。 通常,三阶反对称像差是最重要的,即三叶形和轴向彗形像差,它们都可能由倾斜的电子束引起。 这些优化将产生的分辨率提升取决于显微镜(错误)对准。 如果对齐执行得相当好,高阶像差校正可能对超过 3˚A 分辨率的重建最有用。
几何对齐 包括倾斜系列图像的(刚性)旋转和平移重新对齐,以及整个倾斜序列中单个颗粒的电子束诱导运动的建模。 对于后者,我们忽略了粒子的旋转,只对电子束引起的平移进行建模。 通过这样做,我们可以预先计算每个粒子在其原始粒子周围的每个位置的可能性,然后寻找一种对齐方式,该对齐方式同时最大化所有倾斜序列图像和所有粒子的这些可能性的总和,以及一个先验来确保空间连贯运动。 这允许我们通过查找图像中的单个插值来评估假设粒子位置的可能性。 这里,问题变得等同于最初为单颗粒分析开发的贝叶斯抛光方法,除了包含运动的第三空间维度。
Results
实验一:HIV immature capsid
我们在 cryo-ET 数据集上测试了上述工作流程,该数据集用于确定来自人类免疫缺陷病毒 1 (HIV-1) 的 Gag 多蛋白的未成熟衣壳晶格和间隔肽 1 (CA-SP1) 区域的结构 ) (EMPIAR-10164)。 我们使用了 5 个断层图像的相同子集,这些子集也用于评估 NovaCTF 和 Warp 程序。
引入 3D CTF 校正,并使用 Schur 等人原始分析的对齐参数,NovaCTF 报告了 3.9Å 的分辨率。
Warp 程序在倾斜系列图像中引入了局部和全局运动校正,以及 CTF 参数的优化。 RELION-3 中的 Warp 和 subtomogram 对齐和平均的组合得到了 3.8 Å的分辨率。
我们使用原始分析中的帧对齐后的倾斜系列投影,没有任何其他预处理步骤,以及使用 IMOD 包执行的倾斜系列对齐数据,以及使用 CTFFIND4 进行的 CTF 参数估计。我们使用来自 5 个断层图像子集的 13,320 个粒子,使用原始发布的粒子对齐重建初始参考图,并将其过滤到 5Å。 3D 自动优化中的第一次对齐,然后是初始伪子断层图的平均,得到的分辨率为 3.6Å。 然后将该平均值用于伪子断层图改进和重新调整的完整周期。 我们首先应用 CTF 细化来优化所有粒子的散焦。 这仅略微提高了分辨率。 倾斜系列几何的后续优化,包括模拟局部粒子运动,将分辨率提高到 3.5 Å。 最后,新生成的伪亚断层图的重新对齐导致分辨率为 3.4 Å。 这三个步骤的第二个周期提供 3.3 Å,而第三个周期收敛到 3.2 Å(图 1a)。
进行几何细化以估计局部粒子运动。 考虑变形并没有显示出额外的改进。 在第一个周期中,CTF 和几何的改进最为明显,应用这些优化的顺序并没有改变该数据集的最终结果。对完整数据集的分析生成了一个分辨率为 3.0 ˚A 的结构(未显示),这与使用 M 和 RELION-3 工作流程获得的分辨率相同,并且可能受到 CA 六聚体的灵活性和不对称性的限制。

实验二:Caulobacter crescentus S-layer
第二个实验应用于被称为茎的 C. crescentus 细菌的薄细胞附属物,这些附属物之前已使用cryo-ET 进行成像。 C. crescentus 细胞的细胞体和细胞茎被称为表面层(S 层)的近六边形准晶阵列覆盖。 结合使用 X 射线晶体学、冷冻电镜单颗粒分析和子断层图平均,解析了 S 层的结构,揭示了 S 层如何通过称为脂多糖 (LPS) 的丰富糖脂附着在细菌细胞上。 以前,S 层的低温 ET,使用剂量对称方案收集的 110 倾斜系列,产生了 51,866 个 S 层的六聚体。
使用以前描述的 subtomogram 平均方法,该方法基于在 AV3 Matlab 套件中实现的约束互相关方法,专门为分析排列在晶格中的大分子进行了优化,S层 获得了7.4 ˚A的重建,其中解析了α-螺旋。 通过应用 NovaCTF 改进了这种重建,获得了 4.8 ˚A 的重建,其中大的氨基酸残基侧链被解析。 此外,在 S 层推定的 LPS 结合残基附近观察到 LPS 分子的密度,这与体外重组复合物的cryoEM 单颗粒结构一致。
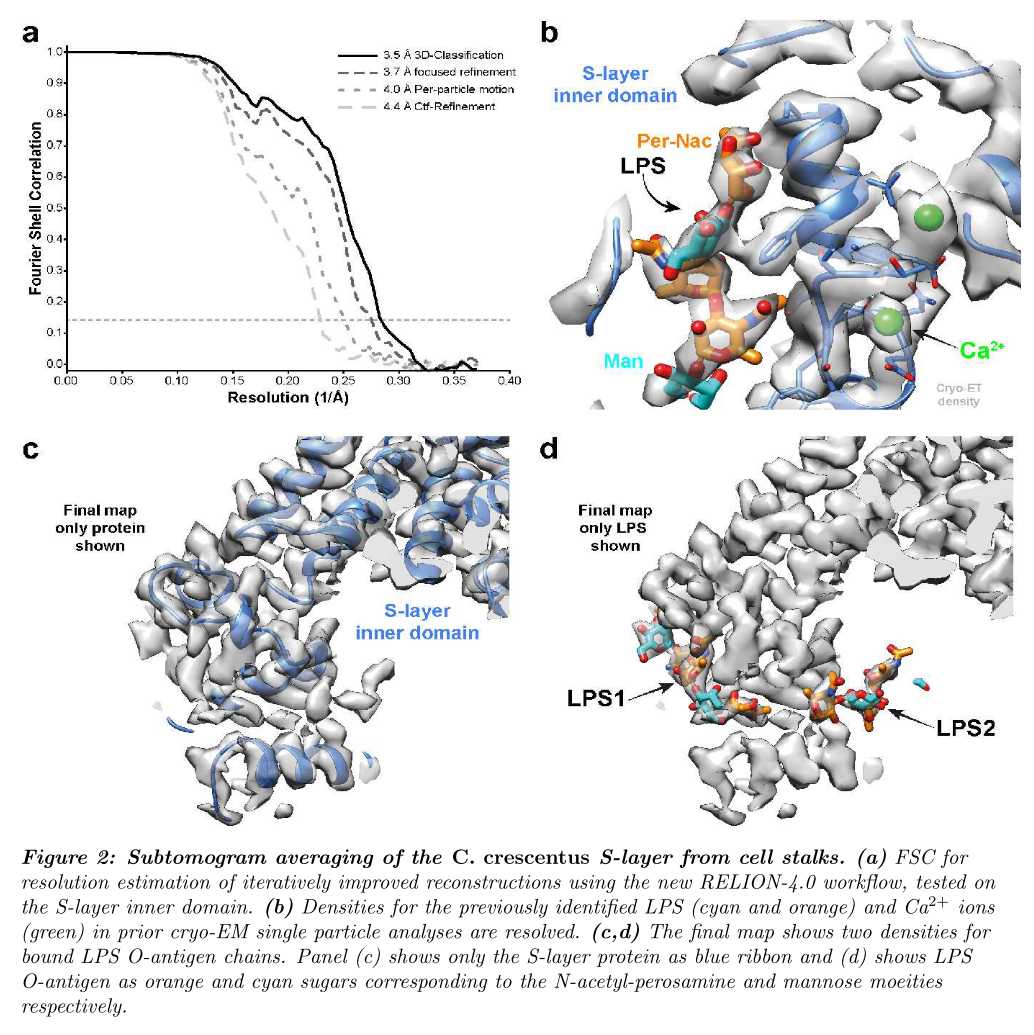
我们使用了初始分析中的帧对齐后的倾斜序列,没有额外的预处理,以及在 IMOD中执行的倾斜序列对齐、来自 CTFFIND4 的 CTF 参数以及欧拉角分配和来自原始分析的子断层图坐标。 这些参数被导入 RELION-4.0,然后是多个周期的伪子断层图生成和细化,类似于上述 HIV 数据集,获得了 S 层六聚体的 5.6 ˚A 重建(图 2a)。 接下来,在 S 层的中心孔周围定义了一个掩码,对应于绑定到 LPS 的内部域,以执行重点细化。另一个周期的伪子断层图重建、CTF 细化和新掩模内的细化将分辨率提高到 4.4 ˚A。考虑到每粒子运动以及额外的伪子断层图改进和细化周期,将中心孔的分辨率提高到 4.0 ˚A,将 S 层的内部域提高到 3.7 ˚A。没有对齐的进一步 3D 分类确定了 42,990 个子断层图的子集,这些子图对内部 S 层进行了 3.5 ˚A 分辨率的重建。 3.5 ˚A 图与体外重组复合物的单颗粒结构非常一致,包括 LPS 结合位点。此外,已知与内部 S 层紧密结合的二价金属离子被解析(图 2b)。令人惊讶的是,在较低的等值面轮廓水平上,我们还观察到了第二个 LPS 结合位点(图 2c-d)。这种密度的大小和形状与 LPS O 抗原的结构一致,说明了 RELION-4.0 中改进的亚子断层图平均有助于探索新的生物学。
讨论
我们在基于二维实验数据的统计模型的经验贝叶斯框架中制定了对层析倾斜序列中多个相同粒子进行平均的问题。事实证明,相同的统计框架在减少可调参数的数量和从单粒子数据中获得高质量重建方面是有效的。二维数据模型比使用 3D 重建子断层图作为中间图像的替代方法更好地描述了实验图像。 中间 3D 数据模型的一个问题是缺失楔校正的需要,这是由于观察到在三个维度上不完整地采集了实验图像。通过根据缺失楔的方向分离粒子,与缺失楔校正相关的伪影可能会影响不同结构状态的分类。通过使用 2D 数据模型,不再需要缺失楔校正。相反,该问题接近于单颗粒分析,其中来自不同方向和不同结构状态的投影被同时整理出来。
如果通过原始粒子的方向分布对不同类别颗粒的 3D 傅里叶变换进行完全采样,则似然优化技术在解决单颗粒分析中的这个问题方面非常成功。 因此,当粒子集合中存在多个不同的结构状态时,这里介绍的方法可能比现有的亚子断层图平均方法特别有利。在实践中,RELION-4.0 中的实现不使用二维投影图像堆栈作为执行对齐和分类的细化程序的输入。 相反,引入了伪子断层图像的概念,其中倾斜序列图像经过傅里叶变换,与它们的 CTF 预乘,并根据当前对倾斜序列几何的最佳估计作为切片插入到 3D 傅里叶体积中。为了接近观察单个 2D 倾斜系列图像的可能性,来自 3D 伪子断层图像的可能性计算需要单独存储 CTF 的累积平方,以及跟踪傅里叶空间中每个像素的采样频率。
在傅里叶变换的无限精细采样的限制下,得到的似然函数与精确的似然函数仅相差一个恒定的偏移量。 伪子断层图的使用允许在 RELION 中重新使用现有代码进行子断层图平均,而 2D 图像的输入堆栈则需要大量的软件开发工作。 然而,在未来,人们可能仍会选择实现真正的 2D 版本的代码,因为在当前常见的断层扫描设置下,要检查的傅里叶像素数量以及计算成本将会降低。 具体来说,当倾斜图像的数量与以像素为单位测量的粒度相比较小时,2D 实现更有效。
除了单个粒子的对齐和分类,这里描述的方法还处理描述倾斜系列的光学和几何特征的参数的重新估计。 一旦获得了初始平均结构,就可以利用其增加的信噪比来比单独从原始倾斜系列图像更准确地确定这些参数。 RELION-4.0 中的实现再次遵循之前为单颗粒分析实现的实现,其中 CTF 细化用于重新估计倾斜序列图像 CTF,并且使用类似于贝叶斯抛光的算法来重新估计倾斜序列对齐,以及整个倾斜系列采集过程中单个粒子的运动。 由于更好的倾斜系列参数将允许更好的伪子断层图,粒子对齐和分类随着倾斜系列参数的优化而迭代。
类似的倾斜序列和 CTF 优化方法已在程序 M 中实现。与 M 相比,RELION-4.0 使用计算效率更高的 C 算法,不需要 GPU 的计算能力。然而,在断层扫描和 SPA 中,RELION-4.0 仅模拟粒子的电子束诱导平移,而 M 也模拟光束诱导的旋转。由于 SPA 在没有对光束引起的旋转进行建模的情况下通常会达到 2 ˚A 分辨率,因此我们假设整个倾斜系列中单个粒子的旋转效果不足以保证在典型的断层扫描分辨率下对其进行校正。在数据确实允许异常高分辨率且可用 GPU 的情况下,在 RELION 中对单个粒子进行对齐和分类之后,M 仍可用于后处理步骤。为了与这里提出的伪子断层图一起工作,对 M 的调整很可能会导致两个程序之间的协同作用增加。同时,将 M 参数转换为 RELION-4.0 的外部工具已经可用(https://github.com/joton/reliontomotools)。
除了减少作为贝叶斯方法特征的可调参数之外,通过实施图形用户界面进一步促进了该领域新研究人员的采用。该接口已广泛用于单颗粒分析,并已扩展用于 RELION-4.0 中的断层数据处理。除了单粒子分析用户熟悉的计算,例如3D分类、3D初始模型生成、3D自动细化,新界面还提供了对CTF细化和贝叶斯抛光的断层扫描特定版本的便捷访问,以及计算伪亚断层图和导入数据的预处理操作和来自 IMOD 中预处理操作的元数据。为了进一步促进社区对这个新软件的采用,我们提供了一个在线教程,该教程使用公开的 HIV 未成熟衣壳数据集来描述和说明获得图 1 中描述的结果所需的所有步骤。
总而言之,我们引入了新的子断层图平均方法,以达到足以进行从头原子建模的分辨率,并增加了这种新兴技术的可访问性。 我们设想我们的方法将允许更多的研究人员从断层扫描数据中计算出更好的结构,这将有助于结构生物学的下一次革命,其中大分子复合物不是孤立地成像,而是在其生物学相关环境中成像。
附加材料:
CTF Refinement
RELION-4.0 中的 CTF 细化优化了以下参数:比例、散焦、散光和高阶(偶数和奇数)光学像差。 因为,除了散焦的差异,相同的 CTF 需要对整个粒子显微照片有效,因此可以像在单颗粒分析算法中一样应用类似的优化。 首先使用线性变换将所有相关信息合并为最小形式,然后在该最小形式上执行最终的(通常是非线性的)优化。
我们将粒子 p 的帧 f 的 CTF 公式化为如下:
C
T
F
p
f
(
j
)
=
−
α
f
τ
f
(
j
)
sin
(
γ
p
f
(
j
)
)
exp
(
i
ρ
f
(
j
)
)
\mathrm{CTF}_{p f}(\mathbf{j})=-\alpha_{f} \tau_{f}(\mathbf{j}) \sin \left(\gamma_{p f}(\mathbf{j})\right) \exp \left(i \rho_{f}(\mathbf{j})\right)
CTFpf(j)=−αfτf(j)sin(γpf(j))exp(iρf(j))
其中
α
f
α_f
αf 描述了整体比例因子,
τ
f
(
j
)
τ_f(\mathbf{j})
τf(j) 是由 Grant 和 Grigorieff 定义的经验辐射损伤模型,
γ
p
f
(
j
)
γ_{pf}(\mathbf{j})
γpf(j) 是对称相位延迟分量,
ρ
f
j
ρ_f{\mathbf{j}}
ρfj 是反对称相位延迟分量。 请注意,只有
γ
γ
γ 在粒子之间变化,因为它包含取决于粒子位置的二次散焦项。 相位延迟的参数化方式与 RELION-3 中的单颗粒分析相同——作为明确命名的低阶项和高阶 Zernike 多项式的组合:
γ
p
f
(
j
)
=
π
λ
j
⊤
D
p
f
j
+
π
2
C
s
λ
3
∣
j
∣
4
−
χ
f
+
∑
Z
n
m
(
j
)
,
D
p
f
=
[
δ
z
p
+
a
1
a
2
a
2
δ
z
p
−
a
1
]
\begin{aligned} &\gamma_{p f}(\mathbf{j})=\pi \lambda \mathbf{j}^{\boldsymbol{\top}} D_{p f} \mathbf{j}+\frac{\pi}{2} C_{s} \lambda^{3}|\mathbf{j}|^{4}-\chi_{f}+\sum Z_{n}^{m}(\mathbf{j}) \text {, }\\ &D_{p f}=\left[\begin{array}{cc} \delta z_{p}+a_{1} & a_{2} \\ a_{2} & \delta z_{p}-a_{1} \end{array}\right] \end{aligned}
γpf(j)=πλj⊤Dpfj+2πCsλ3∣j∣4−χf+∑Znm(j), Dpf=[δzp+a1a2a2δzp−a1]
如前所述,像散散焦矩阵
D
p
f
D_{pf}
Dpf 被分解为散焦项
δ
z
p
δ_{z_p}
δzp 和两个线性像散项
a
1
a_1
a1 和
a
2
a_2
a2,而
C
s
C_s
Cs 描述显微镜的球面像差,
χ
f
χ_f
χf 是恒定相位偏移(由于振幅对比度和相位板,如果使用相位板),
λ
λ
λ 是电子的波长,
Z
n
m
Z^m_n
Znm 是高阶偶数 Zernike 项。 与单颗粒分析的一个关键区别是散焦项
δ
z
p
δ_{z_p}
δzp 不再是每个粒子的自由参数,而是取决于粒子的已知 3D 位置。 因此,在断层扫描中每个倾斜图像仅估计一次散焦项,并且所有粒子都被用来估计。
比例因子 α f α_f αf 是通过计算每个显微照片的以下两个总和,并将它们相除来估计的(† 符号表示复共轭):
α f = G f H f G f = ∑ p , j 1 σ ∣ j ∣ 2 Re ( X p f j ( C T F p f ′ ( j ) V p f j ( p ) ) † ) H f = ∑ p , j 1 σ ∣ j ∣ 2 ∣ C T F p f ′ ( j ) V p f j ( p ) ∣ 2 \begin{aligned} \alpha_{f} &=\frac{G_{f}}{H_{f}} \\ G_{f} &=\sum_{p, \mathbf{j}} \frac{1}{\sigma_{|\mathbf{j}|}^{2}} \operatorname{Re}\left(X_{p f \mathbf{j}}\left(\mathrm{CTF}_{p f}^{\prime}(\mathbf{j}) V_{p f \mathbf{j}}^{(p)}\right)^{\dagger}\right) \\ H_{f} &=\sum_{p, \mathbf{j}} \frac{1}{\sigma_{|\mathbf{j}|}^{2}}\left|\mathrm{CTF}_{p f}^{\prime}(\mathbf{j}) V_{p f \mathbf{j}}^{(p)}\right|^{2} \end{aligned} αfGfHf=HfGf=p,j∑σ∣j∣21Re(Xpfj(CTFpf′(j)Vpfj(p))†)=p,j∑σ∣j∣21∣∣∣CTFpf′(j)Vpfj(p)∣∣∣2
或者,我们还允许用户将 Lambert extinction 模型的参数拟合到数据中,假设完全平坦的样品具有恒定的厚度。 在这种情况下,断层图像 t 的图像 f 中的 CTF 比例表示为光束亮度 α0、样本法线 nt 和光学样本厚度 κt 的函数。
如果使用此选项,则将数据集中所有倾斜系列的 CTF scale 一起估计。光束亮度 α 0 α_0 α0 是全局建模的,而样本厚度和法线在断层图像之间允许是不同的,但在倾斜系列的图像之间则不允许。矢量 z f z_f zf 指向倾斜图像 f 的观察方向。请注意,该模型不允许将几何样本厚度与其消光因子分开,因此我们只能估计两者的乘积。此外,冰法线需要垂直于倾斜系列的估计倾斜轴,因为其指向轴方向的分量与冰厚度或不透明度的增加无法区分……
为了有效地执行散焦估计,我们应用了我们最初为估计单颗粒分析中的高阶像差而开发的优化。 它使我们能够确定一大组粒子的集体偏移量,这些粒子都具有不同的 γ γ γ 值。 具体来说,它允许由改变任何傅里叶像素处的 γ γ γ 值引起的对数似然的变化被表示为一对二维图像,而与粒子的数量无关。 因此,每个粒子的每个像素只需要考虑一次。 之后,可以通过迭代单个图像的像素来评估对数似然。
Geometric Refinement
此方法有两种变体。 如果样本在每个断层图像中包含很少的粒子,则通过预测整个显微照片并计算其与原始照片的互相关来获得最佳结果。 然后,该大互相关图像中的最大值表示最佳图像偏移。 这种方法理论上可以处理任意大的错位。 然而,如果样本非常密集,那么这种全显微照片方法可能会失败。 在这种情况下,通过将方程式中定义的小的每粒子互相关图像相加,并在该总和中找到最大值,可以获得更好的结果。 后一种方法只能校正小于粒子框尺寸一半的未对准,并且它通常在每个断层图像很少粒子的样品上产生较差的结果。
Tips
A u t h o r : C h i e r Author: Chier Author:Chier




























 1435
1435

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










